Уравнение состояния реальных газов

Основные теоретические положения

Уравнение состояния и критическая точка.

Цель работы: изучение поведения реального газа (этана, С₂Н₆) и представление результатов исследования в PV-диаграмме.

Между молекулами реальных газов дей­ствуют как силы взаимного притяжения, так и силы от­талкивания. При весьма малых расстояниях превалируют силы отталкивания, с увеличением расстояний начинают преобладать силы притяжения. Поэтому молекулы ре­ального газа обладают потенциальной энергией, величи­на которой закономерно изменяется в зависимости от расстояния между ними.

 

Рис.1.

Характер рассмотренной кривой показывает, что без большой погрешности левую ветвь ее, соответствующую области действия силы отталкивания, можно заменить вертикальной прямой, распо­ложенной на расстоянии d₀ от оси ординат (рис. 1). Это означа­ет, что силу отталкивания можно считать бесконечно большой, а сами молекулы — твердыми упругими шариками с диаметром do.

Иначе это же самое можно представить так, что каждая молекула окружена упругой сферической оболочкой, недоступной для проник­новения в нее других молекул (а также и сферических оболочек, окружающих эти молекулы).

Значение потенциальной энергии взаимодействия всех
молекул, содержащихся в 1 кг реального газа, можно получить, разбив все

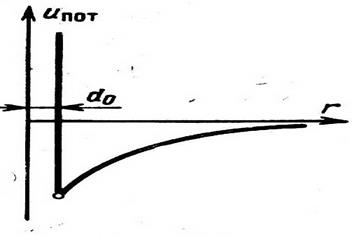
Рис.2.

молекулы на пары и сложив потенциальные энергии парных взаимодействий всех возможных пар. Оче­видно, что это значение зависит от среднего расстояния между молекулами и, следовательно, от удельного объема газа. Таким образом, в про­тивоположность внутренней энергии идеального газа, которая не зави­сит от объема, у реального газа вну­тренняя энергия является функцией удельного объема, а следовательно, давления.

 

Уравнение Ван-дер-Ваальса и его анализ.

Уравнение состояния реальных газов, в основу которого были положены упрощенные, но пра­вильные по существу представления о молекулярно-кинетических свойствах и строении этих газов, было по­лучено в 1873 г. Ван-дер-Ваальсом и носит его имя. Это уравнение имеет вид:

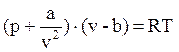(1)

где постоянные а и b зависят от природы газа и у раз­личных газов значительно отличаются друг от друга.

Структура уравнения Ван-дер-Ваальса показывает, что за основу его было взято уравнение состояния иде­альных газов pv = RT, а затем в него были внесены по­правки на объем и давление, которые должны быть при­няты во внимание при изучении реальных тазов.

Одна поправка учитывает объем, недоступный для движения молекул в силу конечности объема самих молекул и наличия взаимодействия между ними. Дело в том, что при беспредельном сжатии газа его объем будет стремиться не к нулю, как у идеальных газов, а к некоторому предельно малому объему b. Величина b больше суммарного объема молекул, так как в связи с наличием сил отталкивания, возникающих при их сбли­жении, молекулы газа при сжатии его не могут быть доведены до соприкосновения. Вокруг каждой молекулы существует как бы сферическая оболочка, в пределы которой не могут про­никнуть другие молекулы. Величина b является суммар­ным объемом таких оболочек и составляет примерно учетверенный объем самих молекул. В связи с этим в уравнение состояние следует вводить не полный объем газа v, а лишь свободный объем v—b.

Другая поправка учитывает силы взаимного притя­жения, действующие в направлении действия внешнего давления и как бы увеличивающие его на некоторую до­бавочную величину, называемую внутренним давлением. Полагая, что внутреннее давление газа изменяется про­порционально квадрату плотности или обратно пропор­ционально квадрату удельного объема газа, Ван-дер-Ваальс принял его равным a/v², где а — коэффициент пропорциональности.

Особенно интересно уравнение Ван-дер-Ваальса тем, что оно качественно отображает главную особенность реальных газов — спо­собность переходить при определенных условиях в жидкое состоя­ние.

Для выявления физического смысла полученных вы­водов рассмотрим в системе координат р— v изотермы, построенные по уравнению Ван-дер-Ваальса (рис.3).Первый случай имеет место при высоких температурах,
когда изотермы имеют вид кривых гиперболического ха­рактера (например, линия1-2). В этом случае

 

Рис.3

каждо­му давлению соответствует вполне определенный удель­ный объем (например, дав­лению р_а соответствует удельный объем v_a). Это значение удельного объёма и является действительным корнем уравнения Ван-дер-Ваальса, оба же мнимых корня в этом случае физиче­ского смысла не имеют и должны быть отброшены. Тело в этом случае при любых давлениях находится в газо­образном состоянии.

Второй случай имеет место при сравнительно низких температурах, когда изотермы имеют два перегиба (на­пример, линия 3-4).

В этом случае между точками е и f находится об­ласть, в которой каждому давлению соответствует три значения удельного объема (например, давлению р_а со­ответствуют удельные объемы , v_c и ), которые и являются тремя действительными и различными корня­ми уравнения Ван-дер-Ваальса.

Участок 3- b соответствует изотермическому сжатию тела, находящегося в газообразном состоянии, причем в точке b оно уже начинает переходить в жидкое со­стояние. Точка d соответствует такому состоянию тела, когда оно уже полностью превратилось в жидкость, в соответствии с чем участок d- 4 представляет собой изо­термическое сжатие жидкости. Точка с соответствует промежуточному двухфазному состоянию тела. Участок кривой b-f. соответствует неустойчивому состоянию пере­охлажденного пара, а участок d-e — также неустойчивому состоянию перегретой жидкости. Что же касается участка e-f, то он вообще физического смысла не имеет, поскольку в действительности при изотермическом сжа­тии тело переходит из газообразного в жидкое состояние при (постоянном давлении, т. е. по горизонтальной ли­нии b-d.

Третий случай имеет место при вполне определен­ной для каждого тела температуре, когда точки b и d, сближаясь с повышением температуры, сливаются в одну точку k, в которой имеет место перегиб соответствующей изотермы, причем касательная к ней в этой точке имеет горизонтальное направление.

Точка к называется критической точкой, а соответ­ствующие ей параметры р_кр, v_кр и T_кр называются кри­тическими параметрами.

Критическая температура, существование которой было открыто в 1861 г. Д. И. Менделеевым, характери­зуется тем, что при температурах выше нее невозможно путем изотермического сжатия добиться перехода газа в жидкое состояние.

(2)

(3)

Критические параметры р и T обычно определя­ются экспериментально (определение v _Kр опытным путем ненадежно), а по ним можно определить постоянные а и b в уравнении Ван-дер-Ваальса для данного газа.

Уравнение Ван-дер-Ваальса можно представить в виде зависимости между безразмерными приведенными параметрами

 

Уравнение Ван-дер-Ваальса в безразмерном или, как иногда говорят, в приведенном виде показывает, что если у разных газов два приведенных параметра имеют одинаковое значение, то одинаковым будет и третий при­веденный параметр. Например, если приведенные дав­ления и температуры двух разных газов равны, то равны и их приведенные удельные объемы.

Состояния разных газов, при которых их приведен­ные параметры π, φ и τ равны, называются соответственными состояниями. Следовательно, если два при­веденных параметра у разных газов рав­ны, то эти газы находятся в соответственных состояниях. Это положение, представляющее собой общую закономерность в изменении состояния ре­альных газов (в предположении, что они подчиняются уравнению Ван-дер-Ваальса), носит название закона со­ответственных состояний.

Реальные газы, находящиеся в соответственных состояниях, являются термодинамически подобными. Это означает, что при одинаковых π, φ и τ свойства всех га­зов в отношении давления, удельного объема и темпера­туры идентичны. Иными словами, если из данных экс­перимента известны свойства какого-либо реального газа, то по ним без всякого эксперимента можно определить аналогичные свойства любого другого газа, находящего­ся с ним в соответственном состоянии.

 

Лабораторная установка и порядок выполнения работы

 

 

 

Ход работы:

Включить электронагреватель с термостатом 1, с помощью регулятора 2 установить нужную температуру. Опыт начинаем тогда, когда температура достигла нужного значения на термометре 5 и стабилизировалась. Значения температур для опытов должны находиться в пределах от 10 до 35 градусов и задаются преподавателем.

С помощью вентиля 3 необходимо выставить нужный объём (шкала 4) и снять показания манометра 6.

Результаты занести в протокол. В графе "Результаты наблюдений" необходимо отмечать моменты появление жидкой фазы этана. Опыт начинать со значения объема 2,5. Шаг изменения принять 0,5 – 0,25 см³ до момента появления жидкого этана и 0,1 – 0,05 см³ после. Опыт заканчивается при достижении предельного давления на манометре.

Опыт необходимо провести 3 раза при разных температурах.

 

Обработка полученных данных и оформление отчета.

 

По формулам (2) и (3) рассчитать коэффициенты a и b для уравнения Ван-дер-Ваальса. Молекулярная масса этана – 30,1 кг/кмоль, параметры критической точки приведены на рис.4. Используя формулу (1) рассчитать давление, используя в качестве аргументов значения удельного объема и температуры, полученные в ходе эксперимента. Расчетные данные заносятся в другую таблицу той же формы.

В масштабе на одной диаграмме построить в PV координатах три изотермы по экспериментальным данным и три изотермы, полученные в результате расчетов.

Рис.4 Примеры различных изотерм для этана.

 

Протокол к лабораторной работе “Уравнение состояния реальных газов”.

 

№ опыта	t 1=	t 2=	t 3=
V	P	Результат наблюдений	V	P	Результат наблюдений	V	P	Результат наблюдений

 

Лабораторная работа