Построение регрессионной модели с фиктивными переменными не чем не отличается от построения множественной регрессионной модели
Для иллюстрации использования фиктивных переменных в пространственных моделях обратимся к приложению Р (таблица Р.1), при этом представленный материал содержит две фиктивные переменные:
D1 – характеризует этаж квартире, при этом 0 присваивается квартире с первым или последним этажом, 1 в противном случае;
D2 – характеризует категорию дома, при этом если дом кирпичный то объекту присваивается 1, цифра 0 в противном случае.
Шаг 1. Запускаем модуль Multiple regression далее в окне Multiple Linear Regression установим галочку в опции Review descriptive statistics, correlation matrix. В окне Review Descriptive Statistic необходимо выбрать вкладку Advanced и нажать кнопку Correlations, в результате чего получаем:
Таблица 9.1 – Матрица парных коэффициентов корреляции
| X1 | X2 | X3 | X4 | X5 | D1 | D2 | Y | |
| X1 | 1,000 | -0,212 | -0,203 | 0,045 | -0,344 | 0,108 | -0,677 | -0,440 |
| X2 | -0,212 | 1,000 | 0,080 | 0,010 | 0,012 | -0,281 | 0,104 | -0,012 |
| X3 | -0,203 | 0,080 | 1,000 | 0,620 | 0,712 | -0,064 | 0,312 | 0,743 |
| X4 | 0,045 | 0,010 | 0,620 | 1,000 | 0,265 | 0,049 | 0,005 | 0,518 |
| X5 | -0,344 | 0,012 | 0,712 | 0,265 | 1,000 | 0,107 | 0,282 | 0,562 |
| D1 | 0,108 | -0,281 | -0,064 | 0,049 | 0,107 | 1,000 | -0,075 | 0,141 |
| D2 | -0,677 | 0,104 | 0,312 | 0,005 | 0,282 | -0,075 | 1,000 | 0,599 |
| Y | -0,440 | -0,012 | 0,743 | 0,518 | 0,562 | 0,141 | 0,599 | 1,000 |
Согласно приведенной таблице получаем, что наибольшее влияние на зависимую переменную Y (см. столбец Y) оказывают показатели X3 (rX2Y=0,743), X4 (rX4Y= 0,518), X5 (rX5Y= 0,562)и D2 (rD2Y= 0,599). При этом необходимо указать на присутствие мультиколлениарности в данных.
Шаг 2. Переходим в стартовое окно модуля и устанавливаем галочку в опции Advanced options. Выбираем кнопку Variables в качестве зависимой переменной указываем Y в качестве независимых указываем X3, X4, X5 и D2.
Шаг 3. В окне Model Definition в прокрутке Method выберем Backward stepwise (Метод пошагового исключения) и нажмем ОК. Получаем следующие результаты:
Таблица 9.2 – Показатели адекватности множественного уравнения регрессии с фиктивными переменными
| Value | |
| Multiple R | 0,837 |
| Multiple R? | 0,701 |
| Adjusted R? | 0,692 |
| F(2,66) | 77,444 |
| p | 0,000 |
| Std.Err. of Estimate | 5,573 |
Таблица 9.3 – Результаты оценки множественной линейной регрессии с фиктивными переменными
| Beta | Std.Err. of Betta | B | Std.Err. of B | t(66) | p-level | |
| Intercept | -5,480 | 4,817 | -1,138 | 0,259 | ||
| X3 | 0,616 | 0,071 | 1,202 | 0,138 | 8,697 | 0,000 |
| D2 | 0,407 | 0,071 | 8,944 | 1,556 | 5,748 | 0,000 |
Согласно данным, приведенным в таблицах 9.2 и 9.3, оцененная модель статистически значима по F- критерию Фишера, при этом R2 = 0,701 и указывает на высокую адекватность модели.
Согласно параметрам уравнения получаем, что при увеличении общей площади квартиры на 1 м2 цен увеличивается на 1,202 тыс. USD.
Проинтерпретировать параметр при фиктивной переменной можно следующим образом – цена за 1 м2 в кирпичных домах по сравнению с остальными в среднем выше на 8,94 тыс. USD. Т.е. можно сделать вывод о том, что категория дома оказывает достаточно сильное влияние на стоимость квартиры.
Отобразим на графике линии регрессии квартир в кирпичных домах и остальных, для этого в исходной таблице образуем две новых переменных Y1 и Y2. При этом в поле Long name вносим следующие выражения:
- для Y1 внесем=-5,48+1,202* v3 (выровненные значения для квартир не в кирпичных домах)
- для Y2 внесем=-5,48+1,202* v3 +8,944 (выровненные значения для квартир в кирпичных домах)
Дале в главном меню Graphs ® 2D Graphs ® Scatterplots в появившемся окне 2D Scatterplots выберем кнопку Variables и укажем в поле X: - X3, а в поле Y: - Y1- Y2. Также в этом окне группе Graph Type укажем Multiple, получаем следующий результат:

Рисунок 9.1. – Линии регрессии для моделей зависимости цены квартиры от типа дома
Как видим, приведенные уравнения отличаются друг от друга только свободным членом, а линии регрессии параллельны.
9.4. Выявление сезонности с использованием сезонных фиктивных переменных в модуле Multiple regression
Для выявления описания сезонных колебаний на практике используют фиктивные переменные. При этом модель имеет следующий вид:
 = а0 + а1t + c2Z2 + c3Z3 + c4Z4 + et (9.1)
= а0 + а1t + c2Z2 + c3Z3 + c4Z4 + et (9.1)
где:

а0, а1, с2, с3, с4 - коэффициенты модели;
В приведенной формуле 1-й квартал взят в качестве эталонной категории, а фиктивные переменные позволят оценить разницу в уровнях сезонности между эталонным кварталом и остальными.
Регрессионная модель, описывающая динамику уровней ряда, относящихся к эталонному 1-му кварталу, примет вид:
yt=a0+а1t
соответственно для наблюдений
2-го квартала yt=a0 + а1t +c2;
3-го квартала yt= a0 + а1t +c3;
4-го квартала yt= a0 + а1t +c4;
Переход из одного квартала в другой будет отражаться лишь в изменении свободного члена регрессионного уравнения и не будет касаться значения параметра b, определяющего угол наклона линейного тренда и характеризующего средний абсолютный прирост уровней ряда под воздействием тенденции.
Найденные значения коэффициентов с2, с3, с4 позволяют оценить «сдвиги» в уровнях за счет фактора сезонности относительно i -го, эталонного квартала. Можно усреднить четыре полученные линии регрессии:
 (9.2)
(9.2)
Тогда расстояние между отдельной регрессионной прямой для любого квартала и усредненной моделью, даст оценку сезонных отклонений в этом квартале. Очевидно, что для аддитивной модели сумма сезонных отклонений будет равна нулю.
Рассмотрим реализацию применения фиктивных переменных для моделирования сезонных колебаний в пакете STATISTICA.
В качестве исходных данных используем квартальный ряд динамики ВВП (приложение Р, таблица Р.2) с 1 квартала 1999 г. до 4 квартала 2004 г.
Шаг 1. Для начала проведем визуализацию ряда, для этого в главном меню программы выберем Graphs ® 2D Graphs ® Line Plots (Variables). После выбора переменной (кнопка Variables) на основе которой необходимо построить график (в данном случае это переменная Y), получаем следующий результат:

Рисунок 9.2 - Динамика ВВП России 1 квартала 1999г-4 квартал 2004г
Согласно приведенному графику наблюдается значительный рост показателя за анализируемый период, а также сезонность с пиком в каждом 3 квартале года.
Шаг 2. Для описания сезонных колебаний создадим 4 фиктивных переменных. Для этого переходим в рабочую таблицу и образуем, переменную t – характеризующую моменты (периоды) времени переменные и переменные Z2, Z3 и Z4 – характеризующие сезонность в анализируемом ряду:

Рисунок 9.3 – Рабочая таблица с набором фиктивных переменных (приведена часть исходного окна)
Шаг 3. В главном меню выберем: Statistics ® Multiple Regression (Статистика ® Множественная регрессия). В появившемся окне Multiple Linear Regression необходимо нажать кнопку Variables (Переменные) и указать в качестве зависимой переменной (Dependent var.) Y, а в качестве не зависимых (Independent var.) переменных - t, Z2, Z3 и Z4.
Нажав кнопку ОК, перейдем в следующее окно, содержащее результаты построения модели.
Шаг 4. В появившемся окне Multiple Regression Results выберемкнопку Summary: Regression results (Итоги: Результаты построения регрессии) перейдем к двум таблицам содержащим оцененные параметры модели и основные показатели адекватности построения регрессии.
Таблица 9.4 – Показатели адекватности модели
| Statistic | Value |
| Multiple R | 0,989 |
| Multiple R? | 0,977 |
| Adjusted R? | 0,973 |
| F(11,144) | 204,893 |
| p | 0,000 |
| Std.Err. of Estimate | 174,096 |
Согласно данным, приведенным в таблице 9.5 полученная модель статистически значима по F -критерию Фишера, но параметр при фиктивной переменной Z2 не проходит тест на статистическую значимость по t-критерию Стьюдента.
Таблица 9.5 – Результаты оценивания сезонной модели
| Beta | Std.Err. of Beta | B | Std.Err. of B | t(19) | p-level | |
| Intercept | 606,006 | 91,247 | 6,641 | 0,000 | ||
| t | 0,956 | 0,035 | 142,156 | 5,202 | 27,327 | 0,000 |
| Z2 | 0,043 | 0,042 | 101,828 | 100,649 | 1,012 | 0,324 |
| Z3 | 0,168 | 0,043 | 398,189 | 101,051 | 3,940 | 0,001 |
| Z4 | 0,125 | 0,043 | 296,600 | 101,718 | 2,916 | 0,009 |
В общем, опираясь на построенную модель можно сказать, что в анализируемом ряду присутствует сезонность, с максимум в 3 квартале каждого года, т.к. b -коэффициент при Z3 имеет наибольшее значение.
Тест (критерий) Г. Чоу
Для выявления структурных изменений в ряду динамики на практике можно прибегнуть к проведению теста Чоу (тесты на устойчивость). Существует несколько модификаций теста Чоу, это тест на обоснованность объединения двух выборок при оценки регрессии и тест на неудачу предсказания. В первом случае тестируется предсказательная способность модели, во втором определяется, происходит ли сдвиг параметров в период предсказания.
В данном случае нас интересует первый подход, рассмотрим механизм его приведения подробнее.
Методика проведения данного теста сводится к следующему: на основе имеющихся данных оценивается уравнение регрессии сначала по всему ряду, а затем уравнения по кусочно-линейной модели.
Далее определяется фактическое значении F -статистики Фишера по формуле:
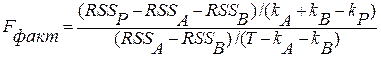 (9.3)
(9.3)
где RSSР – остаточная сумма квадратов модели построенной на основе всего ряда;
RSSА - остаточная сумма квадратов первой модели построенной на основе ряда до момента t* (предполагаемый (или реальный) момент наступления события повлекший структурные изменения ряда);
RSSВ - остаточная сумма квадратов второй модели построенной на основе ряда после момента t*;
kР, kА, kВ – число параметров в регрессии по всему ряду и в первой и второй регрессиях;
Т – число уровней ряда.
Далее с помощью F -статистики тестируется гипотеза H0 о структурной стабильности тенденции изучаемого временного ряда. Для этого найденное значение Fфакт сравнивается с табличным полученным при уровне значимости a и степенями свободы v1 = m; v2=T-k-1. Если Fфакт>Fтабл, то гипотеза отклоняется, а влияние структурных изменений на динамику изучаемого показателя признается значимым.
Для иллюстрации описанной процедуры воспользуемся динамическим рядом ВВП России за период с 1 квартала 1994г. по 4 квартал 2004 года (приложение Р, таблица Р.2).
Шаг 1. Вначале построим уравнение регрессии на основе всей сосвокупности данных. Перед этим необходимо образовать переменную t1 (t1 =0 в 4 квартале 1993 года). Далее запускаем процедуру Multiple Regression.
Шаг 2. В окне результатов оценки модели Multiple Regression Results необходимо выбрать вкладку Advanced и кнопку ANOVA (Overall goodness of fit), тем самым на экран будет выведена таблица с результатами дисперсионного анализа (необходимо заметить, что модель статистически значима по F -критерию Фишера и t -критерию Стьюдента).
Таблица 9.6 – Результаты дисперсионного анализа общей регрессионной модели
| Sums of Squares | df | Mean Squares | F | p-level | |
| Regress. | 433,83 | 0,000 | |||
| Residual | |||||
| Total |
Для оценки F -критерия Фишера (тест Чоу) из данной таблицы понадобится остаточная сумма квадратов, которая находится на пересечении столбца Sums of Squares и строки Residual, т.е. значение 6682327.
Шаг 3. Последовательно оценим две кусочно-линейные модели, первая до 4 квартала 1999г., вторая после данного периода.
Выбор 4 квартала 1999г. как предполагаемый момент наступления события повлекший структурные изменения ряда неслучаен, так как в 1998г. в Россию потряс финансовый кризис который и стал причиной изменения механизма генерации макроэкономических рядов, т.е. начиная с 1999г. (в результате инерционности экономики) имеем совершенно иной динамический ряд который не сопоставим с предыдущей динамикой.
Перед тем как приступить к оценки моделей необходимо ввести две переменные t2 (равна единице в 1 квартале 1994г.) и t3 (равна единице в 1 квартале 1999г.). При построении кусочно-линейных моделей необходимо выбрать кнопку Select Cases и в первом случае указать v0 <21, во втором случае указать v0 >20 (тем самым будут заданы диапазоны для оценки регрессионных уравнений).
В результате оценки будут получены следующие результаты:
Таблица 9.7 – Результаты дисперсионного анализа первой кусочно-линейной регрессионной модели (до 1 кв. 1999г.)
| Sums of Squares | df | Mean Squares | F | p-level | |
| Regress. | 681651,4 | 681651,4 | 200,03 | 0,0000 | |
| Residual | 61339,9 | 3407,8 | |||
| Total | 742991,2 |
Таблица 9.8 – Результаты дисперсионного анализа первой кусочно-линейной регрессионной модели (до 1 кв. 1999г.)
| Sums of Squares | df | Mean Squares | F | p-level | |
| Regress. | 462,40 | 0,000 | |||
| Residual | |||||
| Total |
Шаг 4. Находим расчетное значение F -критерия Фишера:
 =-2706000,12
=-2706000,12
По таблице находим табличное значение F -критерия Фишера при степенях значимости v1 = m= 2; v2=T-k-1 =44-2-1=41, т.е. получаем 3,23.
Сравнивая расчетное значение с табличным, получаем Fфакт>Fтабл, отсюда можно сделать вывод, что подтверждается предположение о значительных изменениях в механизме генерации ряда инвестиций в основной капитал под влиянием финансового кризиса 1998г.
Тесты для самоконтроля
1) Если качественный признак, который необходимо отразить в регрессионной модели имеет четыре градации, то в уравнение включается:
а) четыре фиктивные переменные
б) пять фиктивных переменных
в) одна фиктивная переменная
г) три фиктивная переменная
2) Если качественный признак, который необходимо отразить в регрессионной модели имеет две градации, то в уравнение включается:
а) одна фиктивная переменная
б) две фиктивных переменных
в) три фиктивная переменная
г) нельзя включать качественные переменные в уравнение
3) Приведенный пример расстановки фиктивных переменных используется для:
| Дата | yt | t | t' |
| 1998г. | y1 | -3 | |
| 1999г. | y2 | -2 | |
| 2000г. | y3 | -1 | |
| 2001г. | y4 | ||
| 2002г. | y5 | ||
| 2003г. | y6 | ||
| 2004г. | y8 |
а) элиминирования линейного временного тренда
б) элиминирования тренда в виде параболы второго порядка
в) выделения сезонной составляющей
4) Приведенный пример расстановки фиктивных переменных используется для:
| Дата | yt | t1 | t2 | t3 |
| 1996г. | y1 | |||
| 1997г. | y2 | |||
| 1998г. | y3 | |||
| 1999г. | y4 | |||
| 2000г. | y5 | |||
| 2001г. | y6 | |||
| 2002г. | y8 | |||
| 2003г. | y9 | |||
| 2004г. | y10 |
а) выделения двух прямых, точка пересечения которых известна
б) выделения двух прямых, точка пересечения которых не известна
в) выделения линейного временного тренда
5) Приведенный пример расстановки фиктивных переменных используется для:
| Дата | yt | t1 | t2 |
| 1996г. | y1 | -4 | |
| 1997г. | y2 | -3 | |
| 1998г. | y3 | -2 | |
| 1999г. | y4 | -1 | |
| 2000г. | y5 | ||
| 2001г. | y6 | ||
| 2002г. | y8 | ||
| 2003г. | y9 | ||
| 2004г. | y10 |
а) выделения двух прямых, точка пересечения которых известна
б) выделения двух прямых, точка пересечения которых не известна
в) выделения линейного временного тренда
6) Приведенное выражение  = а0 + а1t + c2Z2 + c3Z3 + c4Z4 + et используют при:
= а0 + а1t + c2Z2 + c3Z3 + c4Z4 + et используют при:
а) построении парного линейного уравнения регрессии
б) описании сезонных колебаний
в) построении нелинейного уравнения
7) Приведенная формула  используется при:
используется при:
а) проверке гипотезы о статистической значимости регрессионного уравнения
б) проверке гипотезы о статистической значимости параметров регрессионного уравнения
в) проверке гипотезы о гетероскедостичности случайных отклонений
г) проверке гипотезы о адекватности линейного тренда построенного на основе всей совокупности
8) Приведенная таблица используется при:
| Периоды | Число наблюдений в совокупности | Остаточная сумма квадратов | Число параметров в уравнении | Число степеней свободы остаточной дисперсии |
| Первое уравнение | n1 | S1ост | m1 | n1-m1 |
| Второе уравнение | n2 | S2ост | m2 | n2-m2 |
| Объединенное уравнение | n | S3ост | m3 | n - m3 = =(n1+n2)-m3 |
а) дисперсионном анализе
б) построении теста Чоу
в) выводе результатов оценки параметров регрессионного уравнения






