Лабораторная работа 10 - Оценка нелинейных регрессионных моделей
Цели и задачи лабораторной работы
В данной лабораторной работе на основе пространственных данных и временного ряда рассмотрим методы оценки нелинейных моделей, при этом выделим следующие задачи:
1) На основе данных об объеме промышленного производства, стоимости основных фондов и среднегодовой численности занятых в промышленности оценить производственную функцию Кобба-Дугласа.
2) На основе ряда численности безработных в РФ оценить параболу второго порядка, гиперболу и логарифмическую прямую.
Определение нелинейной регрессии и основные формы нелинейных моделей
В ходе проведения экономических исследований возникают ситуации, в которых линейные модели не приносят желаемых результатов. В подобных случаях, вероятно, необходимо прибегнуть к использованию нелинейных моделей.
В эконометрических исследованиях различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам (полиномы разных степеней, равносторонняя гипербола).
2) регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная функция).
а) нелинейные модели внутренне линейные;
б) нелинейные модели внутренне нелинейные.
Для оценки параметров нелинейных моделей используются два подхода.
Первый основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.
Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.
Рекомендуемая литература
Для лучшего понимания материала изложенного в данной главе необходимо дополнительно проанализировать следующие источники литературы (см. список использованных источников):
| Номер в списке литературы | Страницы | Номер в списке литературы | Страницы |
Оценка нелинейной модели на основе пространственных данных
В качестве примера нелинейной зависимости рассмотрим класс производственных функции. Которые отражают зависимости, существующие между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т.п. Ярким примером подобных моделей является производственная функция Кобба-Дугласа:

| (10.1) |
где: Y - объем производства,
K - затраты капитала,
L - затраты труда.
Показатели a и b являются коэффициентами частной эластичности. Это означает, что при увеличении одних только затрат капитала (труда) на 1% объем производства увеличится на a% (b%).
Данная функция относится к подклассу 2.1, поэтому данное уравнение можно свести к линейному виду. Для этого берут логарифмы левой и правой частей модели, в результате чего получаем:
lny = lnA+alnK+blnL
Далее заменяем y’= lny, x1= lnK, x2=lnL, получаем
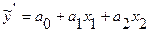
| (10.2) |
а1 – оценка a; а2 – оценка b; а0 – оценка lnA
Для построения производственной функции Кобба-Дугласа в пакте STATISTICA воспользуемся данными по 14 субъектам Приволжского федерального округа (приложение Т, таблица Т.1). В данном пакете программ существует два способа построения нелинейных моделей:
1) Использование модуля Fixed Nonlinear Regression
2) Использование модуля Multiple Regression
10.4.1 Построение нелинейной модели в модуле Fixed Nonlinear Regression
В пакете STATISTICA 6.0 существует специальный модуль Fixed Nonlinear Regression (Фиксированная нелинейная регрессия) предназначенный для оценки нелинейных моделей посредством линеаризации исходных зависимостей.
Для построения производственной функции в данном модуле необходимо:
Шаг 1. В главном меню выберем Statistics ® Advanced Linear/Nonlinear Models ® Fixed Nonlinear Regression (Статистика ® Выбор линейной/нелинейной модели ® Фиксированная нелинейная регрессия).
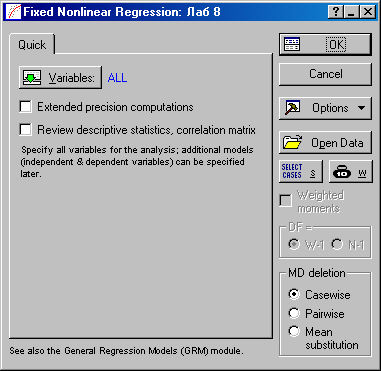
Рисунок 10.1 - Окно установок нелинейной регрессии
где: Extended precision computations - Вычисления с повышенной точностью
Review descriptive statistics, correlation matrix – Обзор описательных статистик, корреляционная матрица
Шаг 2. В появившемся окне Fixed Nonlinear Regression необходимо выбрать кнопку Variables и выделить переменные участвующие в расчете (в данном случае все переменные - ALL).
Шаг 3. В очередном окне Non-linear Components Regression (Компоненты не линейной регрессии) установим флажок напротив опции LN(X), тем самым будут рассчитаны логарифмы для всех переменных участвующих в оценке модели.
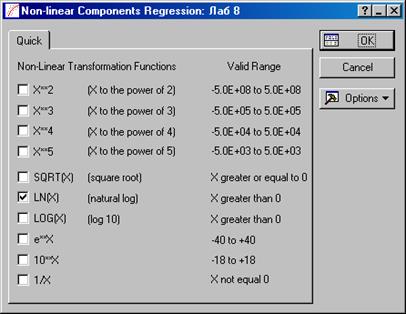
Рисунок 10.2 – Установка процедур линеаризации исходных переменных
Шаг 4. В окне Model Definition (Установки модели) выберем кнопку Variables и сделаем установки как показано на рисунке 3. В качестве зависимой переменной укажем LN-V1 в качестве независимых переменных укажем - LN-V2 и LN-V3.
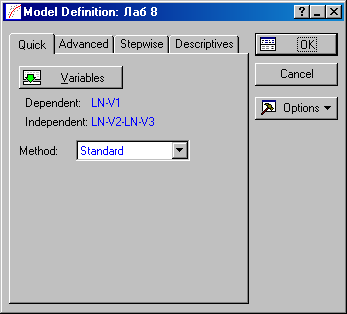
Рисунок 10.3 – Окно выбора зависимой и независимых переменных для построения производственной функции
Рассмотрим результаты оценки производственной функции Кобба-Дугласа.
Согласно данным, приведенным в таблице 2, 98,2% вариации объема промышленного производства описывается вариацией факторов производства, также можно утверждать, что наблюдается сильная связь между исследуемыми показателями.
Таблица 10.1 – Показатели адекватности производственной функции Кобба-Дугласа
| Value | |
| Multiple R | 0,991 |
| Multiple R? | 0,982 |
| Adjusted R? | 0,979 |
| F(2,11) | 308,655 |
| p | 0,000 |
| Std.Err. of Estimate | 0,135 |
Полученная модель статистически значима согласно F -критерию Фишера, параметры модели значимы согласно t-критерию Стьюдента.
Таблица 10.2 – Результаты оценки производственной функции Кобба-Дугласа
| Beta | Std.Err. of Betta | B | Std.Err. of B | t(11) | p-level | |
| Intercept | 1,505 | 0,424 | 3,548 | 0,005 | ||
| LN-V2 | 0,602 | 0,094 | 0,556 | 0,087 | 6,423 | 0,000 |
| LN-V3 | 0,413 | 0,094 | 0,657 | 0,149 | 4,400 | 0,001 |
Интерпретировать полученные показатели можно следующим образом: при изменении стоимости основных фондов на 1%, объем промышленного производства изменится на 0,66%, а при увеличении среднегодовой численности занятых в данном секторе экономики на 1% произойдет увеличение зависимой переменной на 0,56%.
10.4.2 Построение нелинейной модели в модуле Multiple Regression
Прежде чем приступить к оценке функции Кобба-Дугласа вторым способом предварительно преобразуем исходные переменные, а именно рассчитаем логарифмы.
Шаг 1. Образуем новую переменную LN Y (сразу после переменной Y), для этого в поле Long name введем формулу =log10(v1), далее образуем LN K (после переменной K) введя формулу =log10(v3) и LN L (после переменной L) - =log10(v5)
Шаг 2. В главном меню выберем Statistics ® Multiple Regression, при этом в качестве зависимой переменной укажем LN Y в качестве не зависимых - LN K и LN L.
Сравнивая полученные итоговые таблицы с данными приведенными в таблицах 2 и 3 можно убедится в идентичности полученных результатов.






