План урока.
1 Организационный момент, слайд
2. Устный счет (разминка, таблица №8)
3. Актуализация опорных знаний.
§ Проблемная ситуация (задача №1,2,3), слайд
§ Решение задач обязательного уровня по вариантам (I, II).
§ Решение заданий среднего уровня, слайд с решением
4. Подведение итогов обобщения материала.
5. Минута здоровья (гимнастика для глаз)
6. Контроль знаний учащихся по данной теме, проведение проверочной работы с
последующей самопроверкой, слайд.
7. Резервное задание на логическое мышление, слайд
8. Подведение итогов урока, выставление оценок.
9. Домашнее задание по учебнику Богомолов Н.В. (в зависимости от результатов выполнения проверочной работы),
слайд
§ успешно справились – Изучить пункт 33, разобрать примеры №1 и №3 из учебника, выполнить по образцу №417(а,б), № 419 (а,б).
§ допущены ошибки в обязательной части работы - №391-393(а,б)
§ допущены ошибки в дополнительной части работы - №394, 410 (а)
Ход урока
Приветствие
Перед учащимися ставится цель урока, слайд
Мотивируется данная цель, проговаривается выход на конечный результат, итог урока.
Объединить в единое целое понятия: Слово – Символ – Образ
Разминка: таблица №1 для устного счета
Задаваемые вопросы ученикам:
1.Имеет ли смысл выражение:
2. 
2.Верно ли равенство:
3.Найти значение выражения
Актуализация опорных знаний
§ Проблемная ситуация
Задача №1:
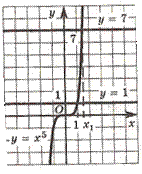
Используя график функции у=х5.
Найти корни уравнения х5=7
 |
Задача №2:
Сколько корней имеет уравнение х4=5
Почему?
Найти эти корни
Задача №3:
Используя график ответить на вопросы:
1. При каком значении параметра а, уравнение имеет
один корень (ответ: при а=0)
2. При каком «а» уравнение имеет два корня?
(ответ: при а>0)
3. При каком «а» уравнение имеет более двух корней
(ответ: ни при каком значении а)
4. При каком «а» уравнение не имеет корней
(ответ: при а< 0)
Решение задач обязательного уровня
Учащиеся решают задания обязательного уровня (карточка оранжевого цвета) по двум вариантам,по очереди проговаривая решение заданий вслух.
Таким образом происходит проверка результатов вычислений, все учащиеся сравнивают свои ответы, происходит коррекция ЗУН.
Карточка (оранжевого цвета)
| Вариант I | Вариант II |
-2 
х4= 81
| -0,5 
у3 = 125
|
Далее решаются задания среднего уровня (карточка синего цвета), работа в малых группах, слайд с ходом решения для самопроверки.
| Решить уравнение, используя способ замены переменной |
Дополнительное задание: Упростите выражение  . Ответ: 2,4
|
Подведение итогов обобщения материала
Ребята, внимание.
Объединить в единое целое: Слово – Символ – Образ, слайд
1. С каким математическим понятием мы работали сегодня – корень n–ой степени
2. Что мы применяли для вычислений корня n–ой степени – свойства
3. Сколько корней имеет уравнение хn=а, если n – нечетное число – один корень
4. Сколько корней имеет уравнение хn=а, если n –четное число – зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
