Цель работы: получение знаний о теоретических основах механики жидкости и газа, закономерностях теплового расширения жидкости; овладение навыками проведения технического эксперимента и обработки его результатов; определение коэффициента теплового расширения воды.
ТЕОРЕТИЧЕСКИЙ МИНИМУМ
Механика жидкости и газа опирается на макроскопическую модель, которая в отличие от молекулярно-кинетической теории рассматривает жидкость или газ, как сплошную текучую среду с непрерывным распределением физических величин, определяющих ее движение и состояние при заданных граничных и начальных условиях.
Согласно макроскопической модели физические характеристики среды (плотность, вязкость, теплопроводность и др.) на молекулярном уровне не рассматриваются. При этом постулируется возможность применения к среде в целом и к ее частям общих законов механики дискретной системы материальных точек (законов Ньютона, сохранения массы, количества движения, момента количества движения, механической и общей термодинамической энергии), из которых и выводятся основные уравнения механики жидкости и газа.
Таким образом, особенностямисплошной деформированной среды (в отличие от теоретической механики) являются сплошность (непрерывность распределения свойств) и текучесть (неограниченная деформируемость).
В силу этих особенностей физические величины, описывающие свойства и состояние среды, определяются через плотность их распределения.
Инерционные свойства среды (масса) характеризуются плотностью среды в данной точке пространства, которая определяется как предел отношения массы среды Δ m, заключенной в объеме ΔΟ, к величине этого объема, когда ΔΟ стремится к нулю:
. (1)
Из (1) масса среды объема Оопределяется как
. (2)
Поверхности среды, имеющие одинаковую плотность во всех точках, называются изостерами.
Поскольку среда обладает сплошностью, то для всех процессов в механике жидкости и газа справедливо уравнение сплошности среды –соотношение, связывающее среднюю скорость частиц среды V с ее плотностью ρ. В случае одномерного движения среды вдоль направления x уравнение сплошности имеет вид:
, (3)
где t –время.
Из (3) следует, что в отсутствие внешнего воздействия на однородную среду (когда 
) плотность сплошной среды не меняется. Однако, она зависит от температуры среды в силу ее температурного расширения – увеличения объема при увеличении температуры.
Температурное расширение капельных жидкостей (примеры капельных жидкостей: вода, нефть, бензин, керосин, масла, спирт и др.) характеризуется коэффициентом температурного расширения βt, выражающим относительное увеличение объема жидкости при увеличении температуры на 1°C:
, (4)
где d Ο– величина изменения объема Ο при повышении температуры на dt. Единица измерения коэффициента температурного расширения: [ βt ]=°C–1.
Перепишем выражение (4) в виде:
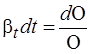. (5)
При условии, что перед началом нагревания температура жидкости равна t0, а занимаемый жидкостью объем – Ο0, решение дифференциального уравнения (5) имеет вид:
. (6)
С учетом малости βt (при температуре от 10 до 20 °С и давлении 105 Па для воды 
°С–1), в линейном приближении:
. (7)
Отсюда получается выражение для зависимости плотности жидкости ρt от температуры t при постоянном давлении:
. (8)
МЕТОДИКА ЭКСПЕРИМЕНТА
Измерения проводятся на установке, состоящей из электрической плитки 1, колбы с водой 2 и термометра 3. Изменение объема фиксируется
|
| Рис. 1. Установка для изучения теплового расширения жидкости. |
измерением высоты столба h жидкости в верхней (узкой) части колбы (см. рис. 1).
Согласно (7) относительное изменение объема жидкости при нагреве воды в колбе равно:
, (9)
где Ο = Ο0+ Ω h, h – высота подъема жидкости, Ω = π d2 /4 – площадь колбы в узкой части, 
– объем колбы без измерительной части (как усеченного конуса), d и D – диаметры верхней части и дна колбы соответственно, h 0 – высота колбы без измерительной части).
Из (9) следует выражение для определения коэффициента теплового объемного расширения:
. (10)
Приборы и принадлежности: колба с водой, шкала для измерения высоты уровня воды, термометр, электрическая плитка для нагревания воды.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. В тетради для отчетов по лабораторным работам запишите название и цель работы, конспект необходимого теоретического минимума, расчетную формулу с выводом и указанием всех физических величин, входящих в нее.
2. Согласно индивидуальной траектории определите диапазон значений температуры, обсудите с руководителем практикума цель и ход эксперимента.
3. Перед началом испытаний с помощью штангенциркуля измерьте диаметры дна и измерительной части колбы (D и d) и высоту h0 в миллиметрах. Результаты измерений занесите в первую строку таблицы результатов измерений
Таблица. Результаты измерений.
| D =_______, мм | d =____, мм | h0 =___, мм | t0 =_______, ᵒ C | ||
| № | t, ᵒ C | h, мм | h/h0 | (t – t0), ᵒ C | βt, ᵒ C–1 |
| n | |||||
| Выборочное среднее |
4. Заполните колбу водой на высоту h0. Вставьте термометр и измерьте начальное значение температуры воды t0 . Результаты измерений запишите в в первую строку таблицы 2.
5. Включите электрическую плитку. Внимательно заносите результаты измерений температуры и высоты столба жидкости в таблицу испытаний 2.
6. Рассчитайте разность температур (t – t0) для каждого измерения, результаты запишите в таблицу.
7. Постройте график зависимости h от(t – t0). Сделайте вывод о характере этой зависимости.
8. По формуле (10) рассчитайте значение температурного коэффициента объемного расширения воды βtдля каждого измерения. Определите выборочное среднее. Результаты занесите в таблицу 2.
9. По формулам (П2) – (П4) определите погрешность измерения Δβt, воспользовавшись алгоритмом обработки и представления результатов многократных измерений, описание которого приведено в Приложении на стр. 55. (Расчеты рекомендуется проводить на компьютере, при этом удобно использовать таблицы Excel).
10. Исследование зависимости плотности среды от температуры осуществляется путем вычислительного эксперимента с помощью электронных таблиц Excel. Для этого в таблицу (см. рисунок 2) надо занести значение коэффициента температурного расширения исследуемой среды и по гистограмме определить, насколько ощутимый вклад вносит данное явление в изменение инерционных свойств среды. Приведите в отчете результаты вычислительного эксперимента и проанализируйте их.
|
| Рис. 2. Моделирование зависимости ρ(t). |
11. В выводе по работе укажите:
1) какое явление наблюдалось в эксперименте;
2) какая характеристика среды была измерена; запишите результат измерения в виде доверительного интервала и надежность полученного результата в форме (П1) (см. Приложение, стр. 55);
3) анализ полученных результатов и эффективности предложенной методики;
4) результаты вычислительного эксперимента и их анализ.
12. Письменно ответьте на контрольные вопросы и выполните задания по работе согласно варианту Индивидуального задания № 1.
Контрольные вопросы
1. Сформулируйте модель объекта, изучаемого в механике жидкости и газа.
2. Дайте определение сплошности и текучести среды.
3. Инструментом любого общетехнического подхода являются основные законы природы. Сформулируйте, каким инструментом пользуется механика жидкости и газа.
4. Каким образом характеризуются состояние и свойства среды в механике жидкости и газа?
5. Как определяется инерционность сплошной среды, если среда однородна и масса m занимает объем Ο?
6. Что можно сказать о среде, изостеры которой являются плоскостями?
7. Запишите уравнение сплошности среды. При каких условиях плотность среды не зависит от времени?
Литература
Гиргидов, А.Д. Механика жидкости и газа (гидравлика): Учебник / А.Д. Гиргидов. – М.: НИЦ ИНФРА–М, 2014. – 704 с. – ЭБС «Знаниум».
Лабораторная работа № 2
