Тема 1. Единицы измерения информации. Системы счисления
Единица измерения информации называется бит (bit) – сокращение от английских слов binary digit, что означает двоичная цифра.
Пример. Если подбросить монету и проследить, какой стороной она упадет, то мы получим определенную информацию. Обе стороны монеты «равноправны», поэтому одинаково вероятно, что выпадет как одна, так и другая сторона. В таких случаях говорят, что событие несет информацию в 1 бит.
Пример. Если положить в мешок два шарика разного цвета, то, вытащив вслепую один шар, мы также получим информацию о цвете шара в 1 бит.
В информатике часто используется величина, называемая байтом (byte),
1 байт = 8 бит.
И если бит позволяет выбрать один вариант из двух возможных, то байт – из 256 (28) вариантов.
Наряду с байтами, для измерения количества информации используются более крупные единицы:
1 Кбайт (килобайт) = 210 байт = 1024 байта;
1 Мбайт (мегабайт) = 210 Кбайт = 1024 Кбайта;
1 Гбайт (гигабайт) = 210 Мбайт = 1024 Мбайта.
1 Тбайт (терабайт) = 240 байта = 1024 Гбайта,
1 Пбайт (петабайт) = 250 байта = 1024 Тбайта.
Содержательный подход к измерению информации
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации х, заключенное в этом сообщении, и число событий N связаны формулой:
. (1)
Решение уравнения (1) имеет вид:
. (2)
То есть именно такое количество информации необходимо для устранения неопределенности из N равнозначных вариантов. Формула (2) носит название формулы Хартли. Получена она в 1928 г. американским инженером Р. Хартли.
Алфавитный подход к измерению информации
При алфавитном подходе, если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ (информационный вес одного символа), вычисляется по формуле (2), где N – мощность алфавита (полное количество символов, составляющих алфавит выбранного кодирования).
В алфавите, который состоит из двух символов (двоичное кодирование), каждый символ несет 1 бит (21) информации; из четырех символов – каждый символ несет 2 бита информации(22); из восьми символов – 3 бита (23) и т.д. Один символ из алфавита мощностью 256 (28) несет в тексте 8 битов информации. Алфавит из 256 символов используется для представления текстов в компьютере. Один байт информации можно передать с помощью одного символа кодировки ASCII. Если весь текст состоит из K символов, то при алфавитном подходе размер содержащейся в нем информации I определяется по формуле:
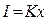, (3)
где x – информационный вес одного символа в используемом алфавите.
Пример. Книга содержит 100 страниц; на каждой странице – 35 строк, в каждой строке – 50 символов. Необходимо рассчитать объем информации, содержащийся в книге.
Страница содержит
35×50 = 1750 байт информации.
Объем всей информации в книге (в разных единицах):
1750×100 = 175000 байт.
175000÷1024 = 170,8984 Кбайт.
170,8984÷1024 = 0,166893 Мбайт.
Вероятностный подход к измерению информации
Формулу для вычисления количества информации, учитывающую неодинаковую вероятность событий, предложил К. Шеннон в 1948 г. Количественная зависимость между вероятностью события р и количеством информации в сообщении о нем x выражается формулой:
. (4)
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить следующим образом – чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Пример. В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании «не глядя» попадется белый шар, больше, чем вероятность попадания черного. Можно сделать заключение о вероятности события, которое интуитивно понятно.
Проведем количественную оценку вероятности для каждой ситуации.
Обозначим pч – вероятность попадания при вытаскивании черного шара, рб – вероятность попадания белого шара.
Тогда
; 
.
Вероятность попадания белого шара в 4 раза больше, чем черного.
Количественная зависимость между вероятностью события р и количеством информации в сообщении о нем x выражается формулой (4). В нашем примере количество информации в сообщении о попадании белого шара и черного шара получится
бит; 
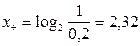бит.
Для определения среднего значения количества информации применяется следующая формула
. (5)
В случае равновероятных выборов 
. Подставляя это значение в формулу (5), получим
. (6)
Пример. При бросании несимметричной четырехгранной пирамидки вероятности выпадения граней равны: 
, 
, 
, 
.
Тогда количество информации, получаемое после броска, будет равно:
бит.
Для симметричной четырехгранной пирамидки количество информации будет
бита.
Заметим, что для симметричной пирамидки количество информации оказалось больше, чем для несимметричной пирамидки.
Системы счисления
Система счисления – набор конкретных знаков-цифр вместе с системой приемов записи, которая представляет числа этими цифрами.
Различные системы счисления могут отличаться друг от друга по следующим признакам:
разные начертания цифр, которые обозначают одни и те же числа;
разные способы записи чисел цифрами;
разное количество цифр.
Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы:
| I | V | X | L | C | D | M |
В числе цифры записываются слева направо в порядке убывания. Величина числа определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей цифры, то она вычитается, если справа – прибавляется.
Пример. VI=5+1=6;
IX=10–1=9;
СССXXVII=100+100+100+10+10+5+1+1=327.
В позиционных системах счисления количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Позиционные системы отличаются друг от друга количеством цифр и поэтому именуются по своему основанию. База системы – это последовательность цифр, используемых для записи числа. Ни в одной системе нет цифры, равной основанию системы.
| Таблица 1 | ||
| Система счисления | Основание | База |
| Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Двоичная | 0, 1 | |
| Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A –10, B –11, C – 12, D – 13, E – 14, F – 15 |
В десятичной системе счисления числа записываются с помощью десяти цифр, т.е. база системы – цифры 0,1,2,3,4,5,6,7,8,9, основание системы р =10. Самая правая цифра обозначает единицы, левее – десятки, еще левее – сотни и т.д.
Восьмеричная и шестнадцатеричная системы счисления используются в ЭВМ как вспомогательные для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используются три двоичных разряда (триада). Для представления одной цифры шестнадцатеричной системы счисления используются четыре двоичных разряда (тетрада).
| Таблица 2 | ||||
| Двоичная (p=2) | Восьмеричная (p=8) | Шестнадцатеричная (p=16) | ||
| триады | тетрады | |||
| A | ||||
| B | ||||
| C | ||||
| D | ||||
| E | ||||
| F |
В любой позиционной системе счисления число N может быть представлено в виде полинома с основанием p:
,(7)
где ai – цифры системы счисления; n и m – число целых и дробных разрядов соответственно; p – основание системы.
Принято представлять числа в виде последовательности цифр:
. (8)
Пример. 
;
.
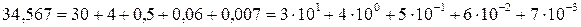В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое – 1. Поэтому основной системой счисления, применяемой в ЭВМ, является двоичная система.
Перевод целого числа из десятичной системы счисления в недесятичную
Чтобы перевести целое десятичное число N в систему счисления с основанием p, необходимо выполнить последовательное деление числа на основание p до тех пор, пока результат не станет меньше p. Последний результат и остатки от деления, взятые в обратном порядке, дают число в необходимой системе счисления.
Пример. Перевести число 164 из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную.
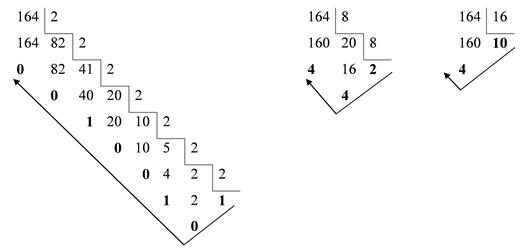
В результате 16410=101001002=2448=А416.
Перевод правильной дроби из десятичной системы счисления в недесятичную
Для перевода правильной десятичной дроби F в систему счисления с основанием p необходимо F умножить на p, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на p, и т.д., до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа F в p -ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной p -ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется 
.
Пример. Перевести число 0,36 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
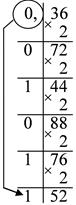0,3610=0,010112
с предельной абсолютной погрешностью 
| 
0,3610=0,2708
с предельной абсолютной погрешностью 
| 
0,3610=0,5С16
с предельной абсолютной погрешностью 
|
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Для перевода восьмеричного (шестнадцатеричного) числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) или четырехразрядным двоичным числом (тетрадой), при этом отбрасывают ненужные нули в старших и младших разрядах.
Пример. Перевести 305,48 
Х2.
Пример. Перевести 7B2,E16 Х2.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример. Перевести 1101111001,11012 Х8.
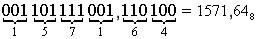
Пример. Перевести 11111111011,1001112 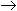Х16.
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести 175,248 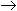Х16.
175,248 = 7D,516.
Перевод из недесятичной системы счисления в десятичную
Для перевода необходимо разложить число по основанию системы счисления, используя формулу (7), и посчитать результат.
Пример. 
;
;
.
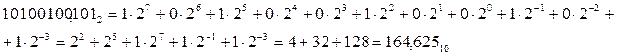Двоичная арифметика
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны – это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
| Таблица 3 | ||
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0–0=0 1–0=1 1–1=0 10–1=1 | 0  0=0
0 1=0
1 0=0
1 1=1
|
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и перенос из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Пример. Выполнить сложение: а) X=11012, Y=1012; б) X=11012, Y=1012, Z=1112.
а)
Результат 11012+1012=100102.
| б)
Результат 11012+1012+1112=110012.
|
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=100102 и Y=1012. Вычислить X–Y.
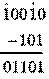
Результат 1001022 – 1012=11012.
Умножение двоичных чисел производится по тем же правилам, что и для десятичных, с помощью таблиц двоичного умножения и сложения.
Пример. Вычислить 10012 1012.
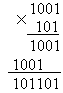
Результат 10012 1012=1011012.
Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.
Пример. Вычислить 1100,0112: 10,012.
Результат 1100,0112: 10,012=101,12.
Задания для выполнения
1. Одна страница книги содержит 25 строк по 80 символов. В книге 30 страниц. Какой объем информации необходим для хранения книги?
2. Определить максимальное количество книг (объемом 300 страниц, на каждой странице 60 строк, 80 символов в строке), полностью размещенных на диске емкостью 600 Мбайт.
3. В текстовом файле хранится текст объемом в 400 страниц. Каждая страница содержит 3200 символов. Если используется кодировка Unicode, то каков будет размер файла?
4. Решить систему уравнений (найти x, y). Указать единицы измерения.
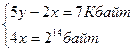
5. Перевести числа в десятичную систему счисления: а) 10110111,10112; б) 1101112; в) 563,448; г) 721,358; д) 1C4,A16; е) 9A2F,B52.
6. Перевести числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную: а) 463; б) 1209; в) 362; г) 3925; д) 11355.
7. Перевести следующие числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную (точность вычислений – 5 знаков после точки: а) 8846,04; б) 725,03125; в) 0,225; г) 0,725; д) 217,375; е) 31,2375; ж) 0,345; з) 0,0625.
8. Перевести числа в двоичную систему счисления: а) 341,48; б) 1725,3268; в) 7BF,52A16; г) 3D2,C16.
9. Перевести числа из одной системы счисления в другую: а) 101,112→Х8; б) 1011110,11012→Х8; в) 1101111101,01011012→Х16; г) 1101010,1001012→Х16.
10.Перевести числа из одной системы счисления в другую: а) 51,438→Х16; б) 312,78→Х16; в) 5B,F16→Х8; г) D4,1916→Х8.
11. В двоичной системе счисления заданы числа X и Y. Вычислить X+Y и X–Y, если: а) X=11001; Y=1011; б) X=101110110; Y=10111001; в) X=100011001; Y=101011.
12. В двоичной системе счисления заданы числа X и Y. Вычислить X´Y и X/Y, если: а) X=1000010011; Y=1011; б) X=1100101; Y=1001; в) X=100101,011; Y=110,1; г) X=100000,1101; Y=101,01.
Контрольные вопросы
1. Какие подходы к измерению информации вам известны?
2. Какова основная единица измерения информации?
3. Сколько байт содержит 1 Кб информации?
4. Приведите формулу подсчета количества информации при уменьшении неопределенности знания.
5. Как подсчитать количество информации, передаваемой в символьном сообщении?
6. Что такое система счисления?
7. Алгоритм перевода из десятичной в недесятичную систему счисления. Примеры.
8. Что такое позиционная система счисления?
9. Алгоритм перевода из недесятичной в десятичную систему счисления. Пример.
10. Двоичная арифметика. Примеры.
