Самостоятельная работа по образцу предполагает решение задач на воспроизведение знаний, умений. Все данные для нахождения искомого, а также сам способ выполнения задания представлены в явном виде в самом задании или в соответствующем алгоритме решения (демонстрация решенных заданий)
Возможные формы отчетности: выполненные задания.
1. Решить следующие дифференциальные уравнения:
 ; ;
|  ; ;
|
 ; ;
|  ; ;
|
 ; ;
|  ; ;
|
 ; ;
| 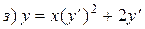 ; ;
|
 ; ;
|  ; ;
|
 ; ;
|  ; ;
|
 ; ;
|  . .
|
Задания для реконструктивной СРС
Характерным признаком этих заданий является то, что в самом задании сообщается общая идея решения, а студенту необходимо развить ее в конкретный способ или способы применительно к условиям задачи. Студент соотносит задание с другими, уже известными ему. При этом главное – актуализация имеющихся знаний, умение отбирать и привлекать необходимые знания для решения задачи
Возможные формы отчетности: конспект выполненных заданий; доклад; реферат; отчет.
2. Найти кривые, обладающие тем свойством, что длина кривой, отсчитываемая от некоторой начальной точки, численно равна площади криволинейной трапеции ограниченной ею.
3. Найти кривую, касательные к которой отсекают на осях координат отрезки, в сумме постоянно составляющие а.
4. Найти кривую, такую, что отрезок, отсекаемый касательной к ней на оси ОУ, равен обратной величине отрезка, отсекаемого той же касательной на оси ОХ.
5. Найти кривые, у которых отрезок нормали между осями сохраняет постоянную длину.
6. Найти кривую, у которой длина отрезка касательной между осями координат постоянна и равна а.
7. Найти общие и особые решения следующих уравнений
 ; ;
|  . .
|
8. Общее решение уравнения имеет вид
 .
.
Найти особое решение.
9. Для семейства кривых у = С (х- С)2 найти огибающую кривую и особое решение уравнения.
Задания для эвристической СРС
Такая работа предполагает создание нестандартных ситуаций, решение нетиповых задач. В ее основе – поиск, догадка, формулирование и реализация идеи решения. Однако поиск имеет частичный характер, необходимый лишь для выполнения какого-либо фрагмента общего задания
Возможные формы отчетности: создание математической модели, отчет по заданной форме; план; конспект; сценарий; продукт деятельности арт-технологий (рисунок); аналитический отчет по заданной форме
10*. Найти дифференциальное уравнение семейства парабол у = х2 - 2Сх.
11*. Найти дифференциальное уравнение семейства кривых
 .
.
12*. Выяснить, каким решением для дифференциального уравнения будет  : частным или особым
: частным или особым

| 
| 
|






