Называются коэффициентами системы, - свободными членами.
2. Решением системы (1) называется набор чисел  , после подстановки которого все уравнения системы (1) становятся числовыми равенствами.
, после подстановки которого все уравнения системы (1) становятся числовыми равенствами.
Система (1) называетсясовместной,еслиона имеет хотя бы одно решение.
Система (1) называется несовместной, если она не имеет ни одного решения.
Пример 1.
Система уравнений  является линейной системой из двух уравнений, содержащей три неизвестные величины
является линейной системой из двух уравнений, содержащей три неизвестные величины  . Коэффициенты системы:
. Коэффициенты системы:  . Свободные члены:
. Свободные члены:  .
.
Эта система совместна, т.к. набор чисел  после подстановки в уравнения системы превращает эти уравнения в числовые равенства
после подстановки в уравнения системы превращает эти уравнения в числовые равенства  .
.
Пример 2.
Система  есть линейная система с двумя неизвестными
есть линейная система с двумя неизвестными  . Эта система не имеет решений. Действительно, если предположить, что какой-то набор чисел
. Эта система не имеет решений. Действительно, если предположить, что какой-то набор чисел  является ее решением,то получим
является ее решением,то получим  и
и  , что невозможно, т.к.
, что невозможно, т.к. 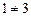 . Следовательно, данная система несовместна.
. Следовательно, данная система несовместна.
Линейная система (1) эквивалентна матричному уравнению
 , (2)
, (2)
где  ,
,  ,
, 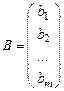
 - матрица размера
- матрица размера  из коэффициентов системы, называется матрицей системы,
из коэффициентов системы, называется матрицей системы,
 - матрица размера
- матрица размера  , называется вектор-столбцом неизвестных,
, называется вектор-столбцом неизвестных,
матрица размера, называется вектор-столбцом свободных членов.
Запись системы (1) матричным уравнением (2) называется матричным представлением линейной системы.
Пример 3. Записать заданные две линейные системы в матричном виде.
1)  , 2)
, 2)  .
.
Решение.
1)  или
или  или
или  ,
,
где  ,
,  ,
,  .
.
2)  или
или  или
или  ,
,
где  ,
,  ,
, 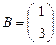 .
.
Особую роль среди систем (1) играют системы, у которых число уравнений (число  ) совпадает с числом неизвестных (числом
) совпадает с числом неизвестных (числом  ), т.е. системы вида
), т.е. системы вида
 (3)
(3)
Такие системы называются линейными квадратными системами или системами  -го порядка. В матричном представлении
-го порядка. В матричном представлении  этой системы присутствуют:
этой системы присутствуют:
матрица системы  - квадратная матрица
- квадратная матрица  -го порядка;
-го порядка;
вектор-столбец неизвестных  и вектор-столбец свободных членов
и вектор-столбец свободных членов 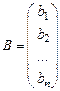 .
.
Определитель  называется главным определителем системы (3). Если
называется главным определителем системы (3). Если  , то система (3) называется невырожденной системой, если же
, то система (3) называется невырожденной системой, если же  , то система (3) называется вырожденной.
, то система (3) называется вырожденной.
Например, система уравнений из примера 2 является вырожденной, т.к. эта система – система второго порядка, и ее главный определитель  равен нулю.
равен нулю.
4.2. Решение невырожденных систем по правилу Крамера и с помощью обратной матрицы.
Перейдем к рассмотрению двух важных методов решения линейных невырожденных систем. Это - метод Крамера и матричный метод.
Метод Крамера вытекает из следующей теоремы. Если главный определитель системы (3) отличен от нуля, то система имеет только одно решение, и это решение можно найти по формулам
 , (4)
, (4)
где  - главный определитель системы,
- главный определитель системы,  - вспомогательные определители, получающиеся из главного определителя
- вспомогательные определители, получающиеся из главного определителя  заменой в нем
заменой в нем  -го столбца столбцом
-го столбца столбцом  свободных членов. Формулы (4) называются формулами Крамера.
свободных членов. Формулы (4) называются формулами Крамера.
Пример 4. Решить методом Крамера систему  .
.
Решение.
Найдем главный определитель системы.
 .
.
Следовательно, заданная система невырождена и имеет только одно решение. Найдем его по формулам Крамера. Для этого вычислим вспомогательные определители  .
.
1)  получается из определителя
получается из определителя  заменой его первого столбца столбцом
заменой его первого столбца столбцом  свободных членов.
свободных членов.
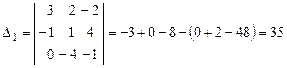 .
.
2)  получается из определителя
получается из определителя  заменой его второго столбца столбцом свободных членов.
заменой его второго столбца столбцом свободных членов.
 .
.
2) 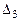 получается из определителя
получается из определителя  заменой его третьего столбца столбцом свободных членов.
заменой его третьего столбца столбцом свободных членов.
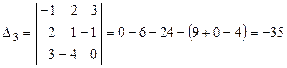 .
.
Согласно формулам Крамера (4) получаем
 .
.
Проверка:  подтверждает правильность найденного решения.
подтверждает правильность найденного решения.
Пример 5. Решить методом Крамера систему  .
.
Решение.
1)  система невырождена и имеет только одно решение.
система невырождена и имеет только одно решение.
2)  ,
,  .
.
3)  .
.
Ответ.  - решение системы.
- решение системы.
Замечание. Если система линейных уравнений (3) вырождена, то метод Крамера не применим. Исследование вырожденных систем проводится другими методами (например, методом Гаусса, изучаемым на занятии 5). Пока же отметим, что вырожденная система либо несовместна, либо имеет более одного решения.
Например, вырожденная система  несовместна (см. пример 2), а
несовместна (см. пример 2), а
вырожденная система  совместна и имеет бесконечно много решений:
совместна и имеет бесконечно много решений:  , где
, где  - произвольное действительное число.
- произвольное действительное число.
Матричный метод решения невырожденных линейных систем, который еще называют методом решения систем с помощью обратной матрицы, заключается следующем.
1. Представим систему (3) матричным уравнением  .
.
2. Найдем матрицу  . Эта матрица существует, т.к.
. Эта матрица существует, т.к.  .
.
3. Умножив слева уравнение  на матрицу
на матрицу  , получим решение в виде
, получим решение в виде
 . (5)
. (5)
Если система (3) вырождена, то матрица  не определена. Поэтому матричный метод решения линейных систем и метод Крамера применимы к одному и тому же классу линейных систем, а именно к множеству линейных невырожденных систем.
не определена. Поэтому матричный метод решения линейных систем и метод Крамера применимы к одному и тому же классу линейных систем, а именно к множеству линейных невырожденных систем.
Пример 6. Решить матричным методом систему из примера 4.
Решение.
1. Заменим систему матричным уравнением  , в котором
, в котором
 ,
,  ,
,  .
.
2.  . Следовательно,
. Следовательно,  существует. Вычисления (их предоставляем читателю, при затруднениях следует просмотреть занятие 3) показывают, что
существует. Вычисления (их предоставляем читателю, при затруднениях следует просмотреть занятие 3) показывают, что  .
.
3. Находим решение по формуле (5).

Таким образом выводим: 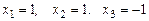 . Этот же ответ получен в примере 4 с помощью правила Крамера.
. Этот же ответ получен в примере 4 с помощью правила Крамера.
Матричный метод применим (помимо невырожденных линейных систем) при решении следующих матричных уравнений:  ;
;  ;
;  , в которых
, в которых  - заданные невырожденные квадратные матрицы,
- заданные невырожденные квадратные матрицы,  - неизвестная матрица,
- неизвестная матрица,  - заданная матрица.
- заданная матрица.
1) В случае  решение получаем после умножения уравнения слева на матрицу
решение получаем после умножения уравнения слева на матрицу  . Ответом будет
. Ответом будет  .
.
2) В случае  решение находится после умножения уравнения справа на матрицу
решение находится после умножения уравнения справа на матрицу  .
.
Ответ:  .
.
3) В случае  надо умножить это уравнение слева на матрицу
надо умножить это уравнение слева на матрицу  и справа на матрицу
и справа на матрицу  . Ответ:
. Ответ:  .
.
Пример 7. Решить матричное уравнение  .
.
Решение. Дано уравнение  , где
, где  ,
,  ,
,  ,
,
 - невырожденная матрица, ее определитель равен 1. Неизвестную матрицу
- невырожденная матрица, ее определитель равен 1. Неизвестную матрицу  находим по формуле
находим по формуле  . Вычисление матрицы
. Вычисление матрицы  опять оставляем читателю. Приведем итоговые результаты.
опять оставляем читателю. Приведем итоговые результаты.
 ,
,  .
.
Пример 8. Решить матричное уравнение  .
.
Решение. Дано уравнение  , где
, где  .
.
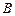 - невырожденная матрица,
- невырожденная матрица,  ,
,  . Вычисление матрицы
. Вычисление матрицы  оставляем читателю.
оставляем читателю.
Неизвестную матрицу  находим по формуле
находим по формуле  .
.
Пример 9. Решить уравнение  .
.
Решение. Имеем матричное уравнение  с матрицами
с матрицами
 .
.
 (см. пример 7).
(см. пример 7).  (см. пример 8).
(см. пример 8).
 .
.
Проверка. Подставим найденную матрицу  в заданное уравнение и убедимся, что полученное произведение трех матриц дает матрицу
в заданное уравнение и убедимся, что полученное произведение трех матриц дает матрицу 
 .
.
_____________________
Домашнее задание.
1. Решить систему  двумя способами
двумя способами
а) с помощью правила Крамера; б) с помощью обратной матрицы.
2. Решить следующие матричные уравнения:
 ;
;  .
.






