Занятие 2. Уравнения с разделяющимися переменными
Цель занятия - развитие у обучающихся личностных качеств, а также направлено на овладение следующими общекультурными компетенциями:
· способностью применять знания на практике;
· способностью приобретать новые знания, используя современные образовательные технологии;
· способностью к анализу и синтезу;
профессиональными компетенциями:
1) в сференаучно-исследовательской деятельности:
· умением понять поставленную задачу;
· глубоким пониманием сути точности фундаментального знания;
· владением проблемно-задачной формой представления математических знаний;
2) в сфере проектной и производственно-технологической деятельности:
· способностью осуществлять целенаправленный поиск информации о научных и технологических достижениях в различных источниках;
· способностью формировать суждения о значении своей профессиональной деятельности;
Проверка теоретических знаний
1. Какой вид имеет уравнение с разделяющимися переменными.
(Уравнение  , где h (y) отлична от нуля всюду на области В, g (x) - определена и непрерывна в В называется уравнением с разделяющимися переменными.)
, где h (y) отлична от нуля всюду на области В, g (x) - определена и непрерывна в В называется уравнением с разделяющимися переменными.)
2. Как производится замена производной на дифференциалы.

3. Разделите переменные в уравнении  .
.
(Деля обе части на h (y) и умножая на dx, получим равенство двух дифференциалов  )
)
4. Если в уравнении g (х) разрывна в некоторой точке х = x и обращается в бесконечность именно в этой точке, а во всех других точках заданной области непрерывна, то, какое решение будет в точке (x, у).
(Общее решение соответствует каждой точке множества  , а в точках (x, у) решение определяется из перевернутого уравнения
, а в точках (x, у) решение определяется из перевернутого уравнения  , т.е. х = x, и присоединяется к решению уравнения, как частное).
, т.е. х = x, и присоединяется к решению уравнения, как частное).
5. В каком случае присоединенное решение оказывается особым.
(Если в каждой точке этого решения нарушается принцип единственности, то такое решение – особое, если единственность сохраняется во всех точках этого решения, то оно является частным.)
6. Сформулируйте теорему из курса математического анализа о равенстве дифференциалов.
(Если выполняется равенство дифференциалов, то их неопределенные интегралы отличаются лишь произвольным постоянным слагаемым)
7. Если уравнение записано в виде  то какая из переменных является функцией.
то какая из переменных является функцией.
(Уравнение допускает выбор в качестве неизвестной функции как у, так и х)
8. Какие ограничения необходимо наложить на функции  .
.
(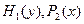 - непрерывны и отличны от нуля всюду на области В,
- непрерывны и отличны от нуля всюду на области В,  - определены и непрерывны в В)
- определены и непрерывны в В)
9. Проведите разделение переменных в этом уравнении.
(Общий интеграл уравнения имеет вид  )
)
Практические задания
Пример 1. Решить уравнение
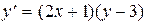 .
.
Решение: Интегрируем его для у ¹ 3
 .
.
Его решение представляет собой функцию
 .
.
Прямая у = 3 - частное решение. С учетом проведенных рассуждений общее решение можно переписать в виде
Ответ:  , у = 3.
, у = 3.
Пример 2. Найти все решения уравнения  .
.
Решение: При 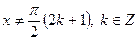 , правая часть определена и непрерывна, поэтому формула
, правая часть определена и непрерывна, поэтому формула

дает общее решение. Прямые  является решением перевернутого уравнения
является решением перевернутого уравнения

причем частным решением и асимптотами общего решения исходного уравнения.
Ответ:  ,
,  .
.






