Интервальной оценкой математического ожидания μ нормального распределения при известной дисперсии  называется интервал
называется интервал
 ,
,  ,
,
удовлетворяющий равенству:  , где: γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание,
, где: γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание, 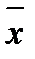 ─ точечная оценка математического ожидания, n ─ объём выборки; число
─ точечная оценка математического ожидания, n ─ объём выборки; число  находится из уравнения
находится из уравнения 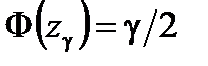 , где
, где  ─ функция Лапласа.
─ функция Лапласа.
Интервальная оценка математического ожидания находится по формуле:
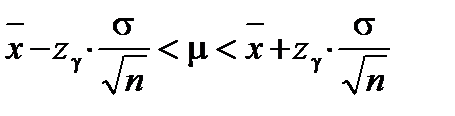 .
.
В MS Excel для вычисления величины  предназначена функция (категория Статистические):
предназначена функция (категория Статистические):
ДОВЕРИТ(Альфа;Станд_откл;Размер),
где: Альфа ─ уровень значимости  , используемый для вычисления уровня надёжности
, используемый для вычисления уровня надёжности 
 . Уровень надёжности равняется
. Уровень надёжности равняется 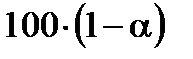 процентам; Станд_откл ─ стандартное отклонение
процентам; Станд_откл ─ стандартное отклонение 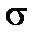 генеральной совокупности, предполагается известным; Размер ─ объём выборки n.
генеральной совокупности, предполагается известным; Размер ─ объём выборки n.
Пример 7. По выборке объёма n =50 найдено значение выборочного среднего  =3,5. Стандартное отклонение равно
=3,5. Стандартное отклонение равно  =2,5. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
=2,5. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
Последовательность выполнения
1. Вычислить уровень значимости: 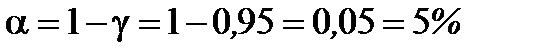 .
.
2. Ввести в ячейку А1 формулу =ДОВЕРИТ(0,05;2,5;50). В А1 появится результат: 0,693.
3. Вычислить границы доверительного интервала:
 ;
;
 .
.
С вероятностью 0,95 математическое ожидание (генеральное среднее) принадлежит интервалу (2,807; 4,193). Математически этот вывод выражается формулой 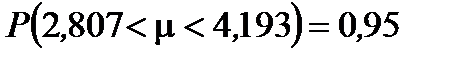 .
.
Интервальной оценкой математического ожидания μ нормального распределения при неизвестной дисперсии 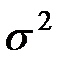 называется интервал:
называется интервал:
 ,
, 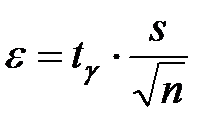 ,
,
удовлетворяющий равенству:  ,
,
где γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание,  ─ точечная оценка математического ожидания,
─ точечная оценка математического ожидания,  ─ исправленная выборочная дисперсия; n ─ объём выборки; число
─ исправленная выборочная дисперсия; n ─ объём выборки; число  находится из уравнения
находится из уравнения  , где
, где  ─ функция распределения Стъюдента.
─ функция распределения Стъюдента.
Интервальная оценка математического ожидания находится по формуле:
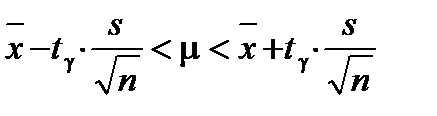 .
.
В MS Excel для вычисления величины  предназначена функция (категория Статистические):
предназначена функция (категория Статистические):
СТЪЮДРАСПОБР(вероятность;степени_свободы),
где: вероятность ─ уровень значимости  ; степени_свободы ─ число степеней свободы
; степени_свободы ─ число степеней свободы 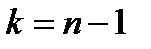 .
.
Пример 8. По выборке объёма n = 20 найдено выборочное среднее  =3,5 и исправленное среднеквадратическое отклонение
=3,5 и исправленное среднеквадратическое отклонение 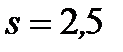 . Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.
1. Ввести в ячейку А1 формулу = СТЪЮДРАСПОБР(0,05;19). В А1 появится результат: 2,093.
2. Вычислить границы доверительного интервала:
 ;
;
 ;
;
 .
.
Доверительный интервал для генерального среднего имеет вид:
 .
.
Доверительный интервал для генеральной дисперсии нормально распределённого признака Х определяется на основе соотношения
 ,
,
где: γ ─ заданная доверительная вероятность,  ─ исправленная выборочная дисперсия; n ─ объём выборки;
─ исправленная выборочная дисперсия; n ─ объём выборки;  и
и  определяются из условий
определяются из условий
 ,
, 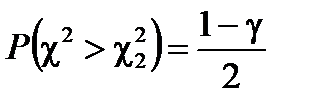
Для вычисления 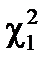 и
и  используется функция
используется функция
ХИ2ОБР(вероятность; степени свободы),
Вероятность ─ значение правой части условий; степени_свободы ─ число степеней свободы  .
.
Пример 9. Количественный признак Х генеральной совокупности распределён нормально. По выборке объёма n = 25 найдено исправленное среднеквадратическое отклонение  . Найти доверительный интервал, покрывающий генеральное среднеквадратическое отклонение
. Найти доверительный интервал, покрывающий генеральное среднеквадратическое отклонение 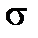 с надёжностью
с надёжностью  .
.
Решение в MS Excel.
1. Вычислить
 ,
,  ,
,  .
.
2. Ввести в ячейки А1 и А2 соответственно формулы =ХИ2ОБР(0,975;24), = ХИ2ОБР(0,025;24). В ячейках появятся результаты: 12,40 и 39,36, то есть  и
и 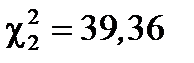 .
.
3. Найти границы интервала
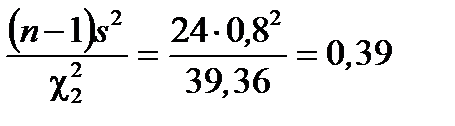 ;
;  .
.
Доверительный интервал с уровнем надёжности 0,95 для генеральной дисперсии  имеет вид 0,39<
имеет вид 0,39<  <1,24. Доверительный интервал для генерального среднеквадратического отклонения находится извлечением квадратного корня 0,62<
<1,24. Доверительный интервал для генерального среднеквадратического отклонения находится извлечением квадратного корня 0,62<  <1,11.
<1,11.
Получение выборочных характеристик
Инструмент «Описательная статистика» используется для получения оценок числовых характеристик распределения генеральной совокупности по случайной выборке из неё. С помощью инструмента «Описательная статистика» можно вычислить следующие параметры:
‒ среднее (статистическую оценку математического ожидания)

‒ стандартную ошибку (среднего)

‒ медиану (Me) – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности;
‒ моду (Mo) – значение изучаемого признака, повторяющегося с наибольшей частотой;
‒ исправленную выборочную дисперсию

‒ Исправленное среднее квадратическое отклонение

‒ Эксцесс

‒ Асимметрию

‒ размах выборки

‒ минимальное значение выборки
‒ максимальное значение выборки
‒ сумму всех значений выборки
‒ объём выборки
‒ наибольшее значение признака, имеющее разность с порядком единиц
‒ наименьшее значение признака, имеющее разность с порядком единиц
‒ уровень надёжности (предельную ошибку выборки)
Уровень надёжности. Флажок устанавливается в том случай, когда необходимо вычислить доверительный интервал для математического ожидания, соответствующий заданной доверительной вероятности (указывается в поле справа в процентах). В таблице результатов появится число, равное половине длины доверительного интервала.
К-наименьший и К-наибольший. Если флажки установлены, то появляются элементы упорядоченной выборки, расположенные на K -ом месте от её начала и от конца.
Пример 10. По полученной на занятии 1 выборке (пример 3) найти оценки числовых характеристик выборки.
Решение
Вызовем инструмент «Описательная статистика» и введём в окне диалога следующие параметры: Входной интервал: $F$1:$F$30; Группирование: по столбцам; Выходной интервал: $B$33. Установим флажки на пунктах Итоговая статистика; Уровень надёжности: 95%; К-наименьший: 2; К-наибольший: 2. Нажмём кнопку ОК и округлим результаты до двух знаков после запятой. Результаты показаны на рис.

Доверительный интервал для математического ожидания нормальной случайной величины при неизвестном среднем квадратическом отклонении имеет вид:
 ,
,
где: число tg определяется с помощью распределения Стъюдента с k = n - 1 степенями свободы; g - доверительная вероятность(уровень надёжности).
Для вычисления значения tg используем функцию СТЪЮДРАСПОБР (вероятность; Степени_свободы). Рассчитаем вероятность - уровень значимости α = 1 - g. Для надёжности 95% α = 1 - 0,95 = 0,05. Вызовем функцию с аргументами:
=СТЪЮДРАСПОБР(0,05; 29). Получим результат: 2,045. Найдём границы доверительного интервала:

(Такое же значение получается в инструменте «Описательная статистика» при вычислении параметра Уровень надёжности).
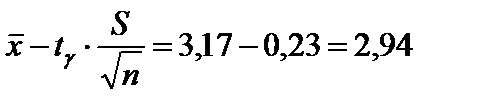 ;
; 
Таким образом, доверительный интервал имеет вид:
 .
.
Задания для самостоятельной работы
Сгенерировать совокупность нормально распределённых случайных величин объёмом N для одной переменной с параметрами µ и s. Из полученной совокупности получить выборку объема n. По выборке построить гистограмму частот (число интервалов k), найти оценки числовых характеристик с использованием инструмента «Описательная статистика», построить доверительный интервал для математического ожидания.
| № варианта | N | 
| 
| 
| k |
| 3,0 | 1,5 | ||||
| 1,5 | 3,0 | ||||
| 2,0 | 1,2 | ||||
| 2,5 | 1,4 | ||||
| 5,5 | 1,3 | ||||
| 4,5 | 1,1 | ||||
| 1,0 | 1,4 | ||||
| 2,5 | 1,2 | ||||
| 3,0 | 1,3 | ||||
| 3,5 | 1,1 | ||||
| 2,5 | 2,0 | ||||
| 4,5 | 1,4 | ||||
| 6,0 | 1,2 | ||||
| 4,0 | 1,3 | ||||
| 5,5 | 1,1 | ||||
| 3,2 | 0,9 | ||||
| 2,2 | 0,8 | ||||
| 2,1 | 0,5 | ||||
| 2,7 | 0,3 | ||||
| 2,3 | 1,1 | ||||
| 3,1 | 0,7 | ||||
| 4,2 | 1,1 | ||||
| 4,4 | 0,8 | ||||
| 4,1 | 0,5 | ||||
| 4,3 | 0,3 |






