1. В соответствии с задачей, указанной преподавателем, прочитать ход ее решения.
2.Произвести необходимые вычисления.
3. Вычисления оформить в виде таблицы.
4. Ответ задачи представить в письменной форме.
Вопросы для самоконтроля.
Как вычислить:
1. Среднее квадратичное отклонение?
2. Коэффициент вариации?
3. Коэффициент корреляции?
4. Среднюю абсолютную и относительную случайную погрешности?
5. Среднюю абсолютную и относительную систематическую погрешности?
6. Среднюю абсолютную и относительную квадратическую погрешности?
Задача №1
На одном из медно-колчеданных месторождений были проведены экспериментальные работы с целью выявить возможность взятия проб бороздой неправильного сечения вместо борозды правильного сечения (3 х 5 см2), которая применялась раньше. Пунктирная борозда отбиралась в виде непрерывного ряда точек, расположенных по мощности рудного тела. Объем частичной пробы из отдельной точки – 27 см3. Вес руды, взятый с 1м рудного тела, 1,5-2кг. Для контроля представительности материала, занятого пунктирной бороздой, сопряженно брались пробы бороздой правильного сечения. Обработка проб и их анализ производились в одних и тех же условиях. Пробы анализировались на медь и серу. Результаты исследования приведены в табл. 4.
Требуется:
1. Определить погрешность и целесообразность применения опробования бороздой неправильного сечения.
Ход решения задачи (по Н. В. Барышеву):
1. Определить по каждому ряду среднее содержание меди и серы способом среднеарифметического (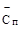
и 
).
Таблица 4
| № п/п | Длина борозды, м | Борозда правильного сечения | Борозда неправильного сечения | ||
| содержание меди Сп | содержание серы Сп | содержание меди Сн | содержание серы Сн | ||
| 1,10 0,80 0,95 1,90 2,30 1,30 2,50 1,95 1,65 1,50 0,60 0,35 1,15 1,00 0,35 0,75 0,30 0,50 0,80 2,00 0,75 0,60 0,70 1,00 1,15 0,60 | 8,97 9,98 7,30 6,51 4,03 0,86 7,48 1,63 4,20 6,84 2,02 4,74 2,25 0,50 0,28 0,99 4,53 0,51 0,37 1,16 0,38 4,82 2,94 1,99 7,91 3,43 | 42,33 45,29 45,08 42.55 43,74 42,31 46,46 43,10 47,35 46,24 24,98 30,23 38,93 46,06 18,43 12,75 34,46 34,01 8,22 40,08 42,89 14,60 20,12 19,62 28,76 24,56 | 9,88 8,85 7,46 6,07 3,55 0,75 7,48 2,84 5,86 7,07 3,37 4,46 3.53 0,31 0,21 1,07 3,44 1,17 0,37 1,07 0,21 4,96 3,05 1,42 7,17 3,21 | 41,68 44,61 54,31 41,14 42,18 40,48 46,44 46,26 46,14 45,80 30.45 30,12 37,01 43,47 18,31 13,50 33,24 39,10 5,35 40 J5 43,27 14,46 17,92 17,84 24,88 24,98 |
2. Определить абсолютные отклонения (∆ С) содержания компонента в каждой пробе (Сп) от среднего содержания (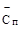) по формуле: ∆ С = Сп – .
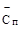3. Вычислить среднее квадратическое отклонение (δ) по формуле:
,
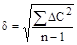где n - число проб.
4. Вычислить коэффициент вариации (V) по формуле:
.
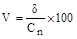5. Вычислить среднюю абсолютную квадратическую погрешность определения среднего содержания m по каждому ряду:
.
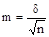6. Вычислить среднюю относительную квадратическую погрешность определения среднего содержания (m %)по формуле:
.
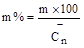7. Сопоставить коэффициенты вариации, вычисленные для каждого ряда проб по меди и сере, и сделать вывод, имея в виду, что при прочих равных условиях коэффициент вариации больше у того ряда, у которого погрешность опробования выше.
8. Вычислить произведения абсолютных отклонений (по общим рядам для меди и серы).
9. Вычислить коэффициенты корреляции для меди и серы по формуле:
.
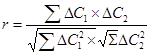10. Проверить надежность корреляционной связи между двумя рядами по формуле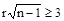 
(при соблюдении указанного неравенства корреляционная связь надежна).
11. Сделать заключение о вероятности появления систематической ошибки при взятии проб бороздой неправильного сечения.
12. Вычислить возможное среднее значение систематической ошибки (f) по формуле:
.
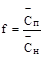13. Определить вероятность систематической ошибки (t) по формуле:
.
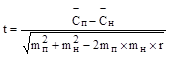Ход решения задачи (по А. П. Прокофьеву):
I. Вычислить абсолютную случайную погрешность (Р) при взятии проб бороздой неправильного сечения по формуле:
.
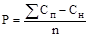2. Вычислить относительную случайную погрешность (Р % по формуле:
.
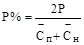3. Определить возможное среднее абсолютное отклонение (систематическое) при взятии бороздой неправильного сечения по формуле:
.
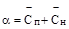Таблица 5
| № п/п | Данные по борозде правильного сечения | Данные по борозде неправильного сечения | ∆Сп ∆Сн | ||
| содержание меди вес %, Сп | абсолютные
отклонения
∆Сп
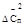(∆Сп = Сп –  )
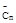| содержание меди вес %, Сн | абсолютные отклонения
∆Сн
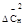(∆Сн = Сн –  )
| ||
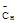| 5,40 5,20 | -0,15 0,0225 -0,25 0,0625 | 5,35 5,80 | -0,25 0,0625 +0,20 0,0400 | +0,0375 -0,05000 | |
| n | ∑Cп | ∑∆C2п | ∑Cн | ∑∆C2н | ∑Cп Cн |
4. Вычислить относительное влияние вероятного систематического отклонения по формуле:
.
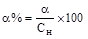При расчете погрешности взятия проб использовать формуляры (табл. 5 и 6).
Таблица 6
| Номер пробы | Содержание меди при взятии проб бороздой | Величина и знаки расхождения Сп – Сн | |
| неправильного сечения, вес %, Сн | правильного сечения, вес %, Сп | ||
| 5,35 5,80 6,07 5,45 | 5,40 5,20 6,20 5,65 | +0,05 -0,60 +0,13 +0,20 | |
| n | ∑Cн | ∑Cп | ∑Cп – Сн |
Примечание. Для определения случайной погрешности ∑(Cп – Сн) вычисляется без учета знака отклонения, а для определения систематической погрешности ∑(Cп – Сн) вычисляется с учетом отклонений явно преобладающего знака.
Задача №2
На одном из месторождений, перед тем как приступить к предварительной разведке, проведен внутренний контроль химических анализов на кобальт. Полученные данные приведены в табл.7.
Требуется определить величину случайной погрешности анализов проб.
Таблица 7
| № п/п | Содержание кобальта по пробам, усл. ед. | № п/п | Содержание кобальта по пробам, усл. ед. | ||
| основным | контрольным | основным | контрольным | ||
Ход решения задачи:
1. Определить абсолютную погрешность химического анализа (по Д.П.Прокофьеву) по формуле:
.
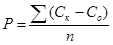2. Определить относительную погрешность химического анализа по формуле:
.
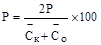3. Выяснять взаимозаменяемость двух рядов химических анализов по формулам:
;
,
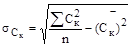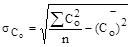где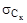 
- абсолютное квадратическое отклонение по контрольным пробам;
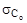- абсолютное квадратическое отклонение по основным пробам;
Ск - среднее содержание по контрольным пробам;
Со - среднее содержание по основным пробам.
4. Определить коэффициент корреляции по формуле:
.
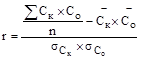5. Определить погрешность вычисления коэффициента корреляции по формуле:
.
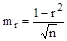6. Сделать заключение о надежности химических анализов. Решение задачи произвести в соответствии с формуляром (табл.8)
Таблица 8
| № п/п | Содержание кобальта по пробам, условные единицы | Квадраты содержания по пробам | Произведе-ние содержаний по конт-рольным и основным пробам Ск × Со | Разность содержаний по контроль-ным и основным пробам Ск — Со | ||
| контрольным Ск | основным Со | контрольным
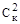
| основным
| |||
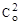
| +2 +1 +1 +2 -7 -1 +2 -1 -3 |
Задача №3
На одном из месторождений ниобия проведен внешний контроль химических анализов. Исходные данные для расчета приведены в табл. 9.
Требуется определить наличие и величину систематической погрешности анализов.
Ход решения задачи:
I. Определить среднее значение относительной систематической ошибки α % (по А.П.Прокофьеву) по формуле:
.
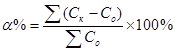2. Определить средние содержание по контрольным Ск и основным Со пробам.
Таблица 9
| № п/п | Содержание ниобия по пробам, условные единицы | |
| контрольным Ск | основным Со | |
3. Вычислить среднее значение систематической ошибки f по формуле:
.
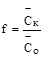4. Вычислить необходимые исходные данные для определения по формулам:
;
;
;
;
;
.
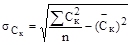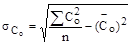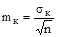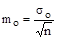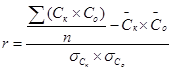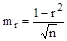5. Вычислить вероятность систематической ошибки t по формуле:
.
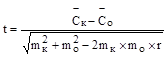6. Сделать заключение о возможности использования основных анализов при подсчете запасов и указать, при каких условиях они могут быть использованы.
Решение задачи произвести в соответствии с формуляром (табл. 10).
Таблица 10
| п/п | Содержание ниобия по пробам, усл. ед. | Квадраты содержания по пробам | Произведе-ние содер-жаний по контроль-ным и основным пробам Ск × Со | Разность содержаний по контроль-ным и основным пробам Ск — Со | ||
| контрольным Ск | основным Со | контрольным
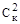
| основным
| |||
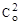
| -5 -2 -4 -3 +1 -4 -7 -5 -1 -4 |
Задача №4
С целью выбора рационального способа отбора проб на полиметаллическом месторождении отобрано 26 сопряженных проб с бороздой правильного сечения 3х5см и пунктирной бороздой. Результаты химических анализов проб проведены в табл. 11.
Требуется: определить возможность отбора на данном месторождении представительных проб пунктирной бороздой, если известно, что отбор проб бороздой правильного сечения здесь вполне обеспечивает их представительность.
Таблица 11
| № пробы | Содержание свинца, % | |
| правильная борозда | пунктирная борозда | |
| 0,32 0,39 0,02 0,18 1,45 2,27 2,00 5,05 4,00 2,09 1,70 1,17 2,76 1,38 2,37 2,16 1,72 0,65 0,80 5,22 2,57 3,06 3,52 1,45 1,43 0,99 | 0,30 0,50 0,05 0,16 1,38 1,70 1,90 4,40 3,89 2,30 1,77 1,22 2,18 1,58 1,98 2,21 1,36 0,73 1,03 5,40 2,41 3,08 2,94 1,38 1,52 0,87 |
Ход решения задачи:
1. По результатам анализа определить для каждого способа отбора проб:
а) среднее содержание свинца;
б) среднеквадратическое отклонение и коэффициент вариации;
в) абсолютные и относительные погрешности определения содержаний.
2. Вычислить коэффициент корреляции двух способов определения свинца и установить наличие или отсутствие систематической ошибки.
3. В зависимости от полученных величин погрешности и коэффициента корреляции решить вопрос о представительности пунктирного опробования.
