Розглянемо обертальний рух матеріальної точки масою  відносно точки О під дією сили
відносно точки О під дією сили  , яка в даний момент часу лежить в площині руху
, яка в даний момент часу лежить в площині руху
(рис.2). Складова сили 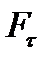 надає матеріальній точці l OiT4wJzJIZEP6JkckkEdEiUnmACjCxgQG+gzjK5qdLyAp8l87pLA/dO9CIaDVxAwXIPcpcklmVyS 4V0SpSq4CBg/Tn4EHnH1AC4UExuVX8gnEjJQCpFLxJN/+DzD4wMJQUE0EQz1BMCJYAxKMJSs4CJe PCmEAamGZ3xaIKjN6PGmlA4Qj2LF56d2P8Nx94Gx7/4HAAD//wMAUEsDBBQABgAIAAAAIQAy/4xQ 4AAAAAgBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8NAEIXvgv9hGcFbu0lrosRsSinqqQi2Qult mp0modndkN0m6b93POntDe/x3jf5ajKtGKj3jbMK4nkEgmzpdGMrBd/799kLCB/QamydJQU38rAq 7u9yzLQb7RcNu1AJLrE+QwV1CF0mpS9rMujnriPL3tn1BgOffSV1jyOXm1YuoiiVBhvLCzV2tKmp vOyuRsHHiON6Gb8N28t5czvuk8/DNialHh+m9SuIQFP4C8MvPqNDwUwnd7Xai1bBLE05qSB5BsH2 U7RIQJxYLNMEZJHL/w8UPwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAA AAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQB AAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQCT/drIKAkAAHhW AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQAy/4xQ4AAA AAgBAAAPAAAAAAAAAAAAAAAAAIILAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAjwwA AAAA ">
надає матеріальній точці l OiT4wJzJIZEP6JkckkEdEiUnmACjCxgQG+gzjK5qdLyAp8l87pLA/dO9CIaDVxAwXIPcpcklmVyS 4V0SpSq4CBg/Tn4EHnH1AC4UExuVX8gnEjJQCpFLxJN/+DzD4wMJQUE0EQz1BMCJYAxKMJSs4CJe PCmEAamGZ3xaIKjN6PGmlA4Qj2LF56d2P8Nx94Gx7/4HAAD//wMAUEsDBBQABgAIAAAAIQAy/4xQ 4AAAAAgBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8NAEIXvgv9hGcFbu0lrosRsSinqqQi2Qult mp0modndkN0m6b93POntDe/x3jf5ajKtGKj3jbMK4nkEgmzpdGMrBd/799kLCB/QamydJQU38rAq 7u9yzLQb7RcNu1AJLrE+QwV1CF0mpS9rMujnriPL3tn1BgOffSV1jyOXm1YuoiiVBhvLCzV2tKmp vOyuRsHHiON6Gb8N28t5czvuk8/DNialHh+m9SuIQFP4C8MvPqNDwUwnd7Xai1bBLE05qSB5BsH2 U7RIQJxYLNMEZJHL/w8UPwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAA AAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQB AAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQCT/drIKAkAAHhW AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQAy/4xQ4AAA AAgBAAAPAAAAAAAAAAAAAAAAAIILAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAjwwA AAAA ">

|

|

|

|

|
| О |

|
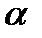
|

|
| Рис. 2. До виведення закону динаміки обертального руху матеріальної точки за умови дії сили у площині обертання. |
 . Тоді
. Тоді  .
.
Дія нормальної складової сили  зводиться лише до надання точці
зводиться лише до надання точці 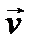 нормального приско-рення (закручування траєкторії). Оскільки за даних умов
нормального приско-рення (закручування траєкторії). Оскільки за даних умов  , то:
, то:

Домножимо вираз на 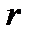 :
:
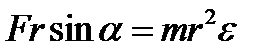 .
.
Увівши позначення 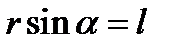 ,
,  ,
,  , запишемо останній вираз у вигляді:
, запишемо останній вираз у вигляді:
 , (2.10)
, (2.10)
де  – момент сили
– момент сили  відносно точки О, l – плече сили,
відносно точки О, l – плече сили,  - момент інерції матеріальної точки
- момент інерції матеріальної точки  відносно точки О.
відносно точки О.
Вираз (2.10) за своїм виглядом є аналогом другого закону Ньютона для криволінійного руху з тією різницею, що аналогом сили  є момент сили
є момент сили  , маси
, маси  – момент інерції
– момент інерції  , прискорення
, прискорення  – кутове прискорення
– кутове прискорення  .
.
Оскільки точка рухається по колу сталого радіуса (r=const), то її момент інерції  також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:
також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:


|

|

|

|

|
Рис. 3 Момент сили  , що діє на матеріальну точку, момент імпульсу , що діє на матеріальну точку, момент імпульсу  матеріальної точки. матеріальної точки.
|
| m |
 називають моментом імпульсу матеріальної точки відносно точки О. Даний вектор, який в умовах цієї задачі чисельно дорівнює
називають моментом імпульсу матеріальної точки відносно точки О. Даний вектор, який в умовах цієї задачі чисельно дорівнює  , є аналогом вектора імпульсу
, є аналогом вектора імпульсу  для прямолінійного руху.
для прямолінійного руху.Розглянемо загаль-ний випадок, коли сила  не лежить в одній площині з існуючою коловою траєкторією. За другим законом Ньютона рівняння руху матеріальної точки маси
не лежить в одній площині з існуючою коловою траєкторією. За другим законом Ньютона рівняння руху матеріальної точки маси  має вигляд:
має вигляд:

 .
.
Вектор  назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор
назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор 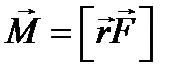 – моментом сили
– моментом сили  відносно точки О.
відносно точки О. 
Вираз  =
=  називають рівнянням моментів.
називають рівнянням моментів. 






