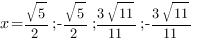Решение квадратных уравнений
Квадратным называется уравнение вида: ax2 + bx + c = 0, a≠0.
a, b, c – коэффициенты уравнения.
Квадратные уравнения
 |  |
Полные Неполные
a, b, c ≠ 0 a≠0, b или/и c = 0
Решение неполных квадратных уравнений.
1) Уравнение вида ax2+bx=0, т.е. с = 0.
Такое уравнение решается вынесением Х в левой части за скобки.
х (ах+b)=0
Используем правило: Произведение равно нулю, когда один из сомножителей равен нулю.
x=0 или ax+b=0
ax=-b
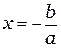
Ответ: 0 и 
Пример:
Ответ: 0 и 1,5.
2) Уравнение вида ax2+c=0, т.е. b = 0.
Такое уравнение решается по формуле разности квадратов, если есть такая возможность. Если такой возможности нет, то уравнение решенией не имеет.
Пример:
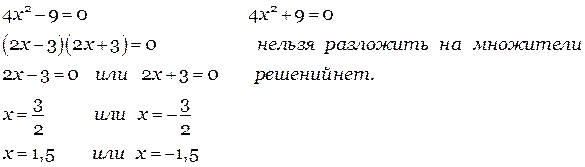
Ответ:{1,5; -1,5}. Ответ: нет решений.
Решение полных квадратных уравнений.
Порядок решения квадратного уравнения:
0) Проверить сумму коэффициентов:
a. a + b + c = 0. Если это выполняется, то один из корней равен 1, а другой с/а.
b. a – b + c = 0. Если это выполняется, то один из корней равен -1, а другой (- с/а).
1) Вычислить дискриминант по формуле:
a. Если D < 0, то корней нет,
b. Если D = 0, то есть два одинаковых корня, которые равны 
c. Если D > 0, то есть два различных корня, которые определяются по формулам:
Теорема Виета
Подбор корней надо начинать с определения знаков корней и перебора делителей числа c/a.
Семь типов рациональных уравнений, сводящихся к квадратным
В этом разделе я покажу вам алгоритмы решения семи типов рациональных уравнений, которые с помощью замены переменных сводятся к квадратным. В большинстве случаев преобразования, которые приводят к замене, весьма нетривиальны, и самостоятельно о них догадаться достаточно трудно.
Для каждого типа уравнений я объясню, как в нем делать замену переменной.
Итак, начнем.
1. (x-1)(x-7)(x-4)(x+2)=40
Заметим, что в левой части уравнения стоит произведение четырех скобок, а в правой - число.
Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.
2. Перемножим их.
3. Введем замену переменной.
В нашем уравнении сгруппируем первую скобку с третьей, а вторую с четвертой,так как (-1)+(-4)=(-7)+2:
В этом месте замена переменной становится очевидной: 
Получаем уравнение 
Ответ: 
2. 
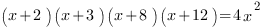
Уравнение этого типа похоже на предыдущее с одним отличием: в правой части уравнения стоит произведение числа на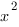 
. И решается оно совсем по-другому:
Группируем скобки по две так, чтобы произведение свободных членов было одинаковым.
2. Перемножаем каждую пару скобок.
3. Из каждого множителя выносим за скобку х.
4. Делим обе части уравнения на .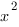
5. Вводим замену переменной.
В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как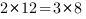 
:
Заметим, что в каждой скобке коэффициент при 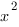и свободный член одинаковые. Вынесем из каждой скобки множитель 
:
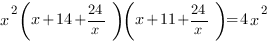
Так как х=0 не является корнем исходного уравнения, разделим обе части уравнения на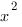 
. Получим:
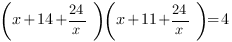
Теперь можем ввести замену переменной: 
Получим уравнение: 
Ответ: 
2. 
Заметим, что в знаменателях обоих дробей стоят квадратные трехчлены, у которых старший коэффициент и свободный член одинаковые. Вынесем, как и в уравнении второго типа х за скобку. Получим:
Разделим числитель и знаменатель каждой дроби на х:
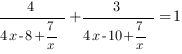
Теперь можем ввести замену переменной:
Получим уравнение относительно переменной t:
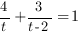
Ответ: 
4. 
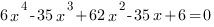
Заметим, что коэффициенты уравнения симметричны относительно центрального. Такое уравнение называется возвратным.
Чтобы его решить,
1. Разделим обе части уравнения на 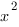(Мы можем это сделать, так как х=0 не является корнем уравнения.) Получим:
2. Сгруппируем слагаемые таким образом:
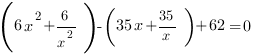
3. В каждой группе вынесем за скобку общий множитель:
4. Введем замену: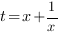 
5. Выразим через t выражение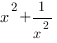 
:
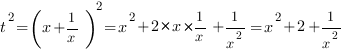
Отсюда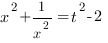 
Получим уравнение относительно t:
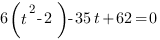
Ответ: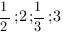 
Однородные уравнения.
Уравнения, имеющие структуру однородного, могут встретиться при решении показательных, логарифмических и тригонометрических уравнений, поэтому ее нужно уметь распознавать.
Однородные уравнения имеют такую структуру: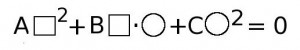 
В этом равенстве А, В и С - числа, а квадратиком и кружочком обозначены одинаковые выражения. То есть в левой части однородного уравнения стоит сумма одночленов, имеющих одинаковую степень (в данном случае степень одночленов равна 2), и свободный член отсутствует.
Чтобы решить однородное уравнение, разделим обе части на 
Или на 
Или на 
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Пойдем первым путем. Получим уравнение:
Сократим дроби, получим:
Теперь мы вводим замену переменной:
И решаем квадратное уравнение относительно замены:
.
Решим уравнение:
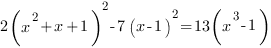
Разложим выражение, стоящее в правой части уравнения на множители.
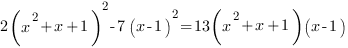
Перенесем все влево, получим:
Теперь мы видим, что перед нами однородное уравнение. Разделим обе части уравнения на 
, предварительно проверив, что х=1 не является корнем исходного уравнения.
Теперь самое время ввести замену переменной:
Получим квадратное уравнение:
Ответ: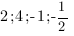 
6. 
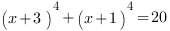
Это уравнение имеет такую структуру:
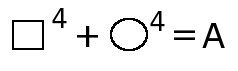
Решается с помощью введения вот такой замены переменной:
В нашем уравнении 
,тогда 
. Введем замену:
Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:
Упростим выражение и получим биквадратное уравнение относительно t:
Ответ: 
или 
7. 
Это уравнение имеет такую структуру:
Чтобы его решить, нужно в левой части уравнения выделить полный квадрат.
Чтобы выделить полный квдарат, нужно прибавить или вычесть удовоенное произведение. Тогда мы получим квадрат суммы ли разности. Для удачной замены переменной это имеет определяющее значение.
Начнем с нахождения удвоенного произведения. Именно оно будет ключиком для замены переменной. В нашем уравнении удвоенное произведение равно
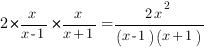
Теперь прикинем, что нам удобнее иметь - квадрат суммы или разности. Рассмотрим, для начала сумму выражений:
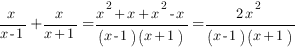
Отлично! это выражении в точности равно удвоенному произведению. Тогда, чтобы в скобках получить квадрат суммы, нужно прибавить и вычесть удвоенное произведение:
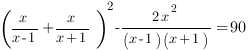
Введем замену: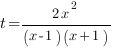 
Получим квадратное уравнение:
Ответ: 
