· Арифметические операции
· Порядок выполнения операций
· Стандартные математические функции
Задание
Составьте программу, которая подсчитывает и выводит значение t1 и t2 по формулам, которые приведены в Вашем варианте индивидуального задания. Определите области допустимых значений параметров формул и задайте произвольные значения из этих областей. Параметры, которые имеют имена n и m — целые, другие параметры — с плавающей точкой. Значения параметров с именами x и y должны вводиться с клавиатуры, значения других — задаваться как начальные значения при объявлении соответствующих переменных.
Допускается (и даже желательно) упростить / разложить формулы для того, чтобы обеспечить минимизацию объема вычислений.
Варианты индивидуальных заданий
| Вариант | Задания | |


| Найти частное t1 и t2 | |

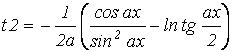
| Определить, что больше t1 или t2 | |


| Определить, что меньше t1 или t2 | |
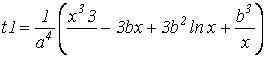

| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 | |
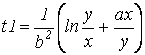 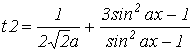
| Определить, что больше t1 или t2 |
 
| Определить, что больше t1 или t2 | |
 
| Найти произведение t1 и t2 | |
 
| Определить, что больше t1 или t2 | |
 
| Найти произведение t1 и t2 | |
 
| Найти частное t1 и t2 | |
 
| Определить, что меньше t1 или t2 | |
 
| Определить, что меньше t1 или t2 | |
 
| Найти разность t1 и t2 | |
 
| Определить, что меньше t1 или t2 |
 
| Найти сумму t1 и t2 | |
 
| Найти произведение t1 и t2 | |
 
| Определить, что больше t1 или t2 | |
 
| Определить, что меньше t1 или t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 | |
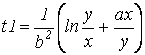 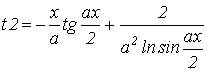
| Определить, что меньше t1 или t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 |
 
| Определить, что меньше t1 или t2 | |
 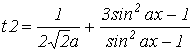
| Определить, что меньше t1 или t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 | |
 
| Найти частное t1 и t2 | |
 
| Определить, что больше t1 или t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти сумму t1 и t2 | |
 
| Определить, что больше t1 или t2 | |
 
| Определить, что меньше t1 или t2 |
 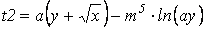
| Найти произведение t1 и t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти частное t1 и t2 | |
 
| Найти произведение t1 и t2 |
Пример решения задачи
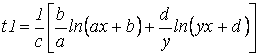 ,
,  .
.
Разработка алгоритма решения
Основной алгоритм
Алгоритм решения задачи — линейный исостоитиз:
· ввода значений x и y;
· вычисления значения t1;
· вычисления значения t2;
· выведения значений t1 и t2.
Оптимизация алгоритма
Перед непосредственным програмированием алгоритма проанализируем, как в нем можно изменить объем вычислений.
Выражение ax встречается один раз в первой формулеи дважды — вовторой. Следовательно, можно один раз произвести умножение a*x, а потом использоватьэтот результат.
Во второй формуле дважды встречается умножение квадратного корня на тангенс — это вычисление можно так же сделать один раз.
Выражение c2–b2 можноразложить на (c+b)(c–b). До разложения в выражении было две операции умножения (возведение в степень 2) и одна — сложения. После разложения — два сложения и одно умножение, что выгоднее для вычислений.






