Лабораторная работа 4
АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ И ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ ПРОИЗВОЛЬНОМ НАГРУЖЕНИИ СТЕРЖНЯ
Цель и содержание работы: изучение видов напряженного состояния впроизвольной точке, приобретение навыков оценки напряженного состояния и определения напряжений при произвольном нагружении.
Теоретическое обоснование
Для оценки вида напряженного состояния в произвольной точке необходимо вычислить главные напряжения в этой точке. Различают объемное (трехосное), плоское (двухосное) и линейное (одноосное) напряженные состояния. При первом из них все главные напряжения отличны от нуля; при втором – одно из главных напряжений равно нулю; при третьем – два главных напряжения равны нулю.
При произвольных исходных площадках главные напряжения находят как корни кубического характеристического уравнения
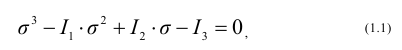
где I1, I2, I3 – коэффициенты уравнения, называемые инвариантами напряженного состояния, определяются по формулам (1.2). При использовании формул (1.2) знак касательных напряжений следует определять по правилу: касательное напряжение считается положительным, если на площадке, внешняя нормаль к которой совпадает с положительным направлением параллельной к этой нормали координатной оси, а само напряжение направлено в сторону положительного направления координатной оси. Согласно этому правилу, все касательные напряжения, показанные на рисунке 1.1, положительные.
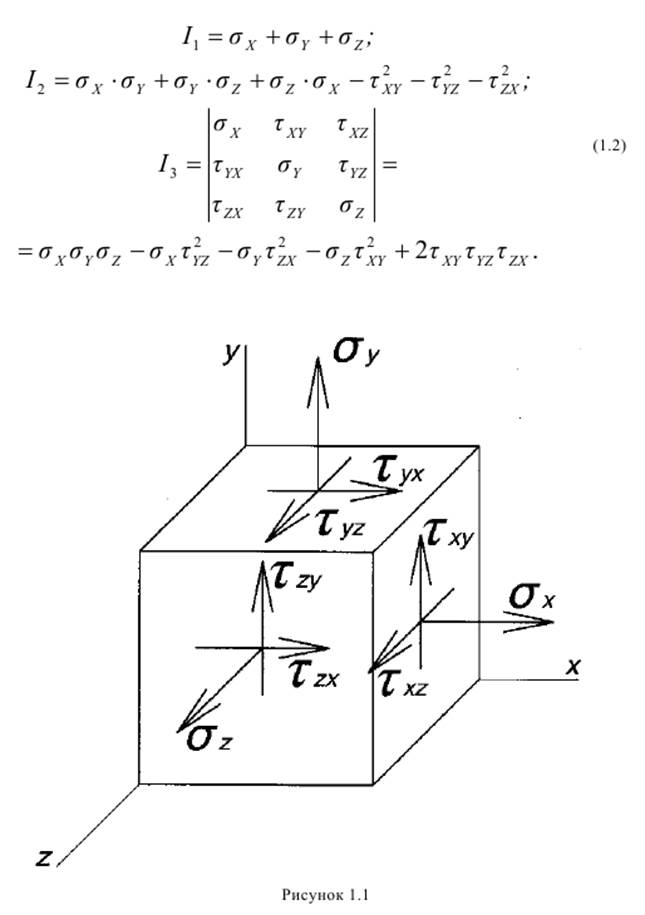
Через главные напряжения инварианты выражаются следующим образом:
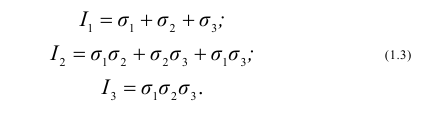
В частных случаях инварианты могут обращаться в ноль. Если, например, I3=0, то один из корней уравнения (1.1) также равен нулю и, следовательно, напряженное состояние является плоским (двухосным). Если же равны нулю инварианты I2 и I3, то уравнение (1.1) имеет два нулевых корня, а напряженное состояние будет линейное или одноосное.
Корни характеристического уравнения (1.1) могут быть найдены по точным формулам (формулы Кордано), или приближенно, например, численным методом Ньютона. Индексы расставляют так, чтобы было соблюдено условие σ1 ≥σ2 ≥σ3 (неравенства алгебраические;напряжения растяжения считаются положительными). Для данной точки σ1 наибольшее, а σ3 наименьшее в алгебраическом смысле нормальные напряжения.
После вычисления главных напряжений максимальные касательные на-пряжения определяют по формуле (1.4)
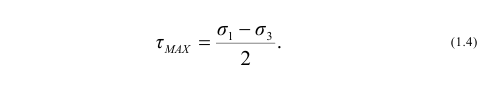
Положения главных площадок по отношению к исходной координатной системе определяются следующим образом. Вносим значение σ1 в любые два уравнения (1.5) и присоединяем к ним в качестве третьего уравнение (1.6)
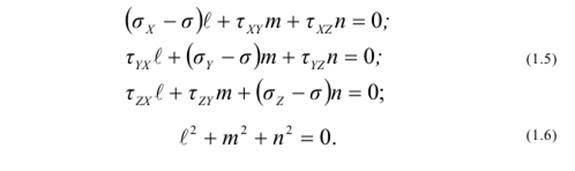Получаем систему трех линейных уравнений, из которых находим значения направляющих косинусов ℓ1, m1, n 1, определяющих положение площадки с напряжением σ1.
Аналогично находятся направляющие косинусы площадок с главными напряжениями σ2 и σ3, при этом все три главные напряжения будут взаимно перпендикулярны.
Площадки, равно наклонные ко всем трем главным площадкам, называются октаэдрическими, соответствующие нормальное и касательное напряжения также называют октаэдрическими. Для их определения служат формулы
Нормальное и касательное напряжения на площадке общего положения, не параллельной ни одному из главных напряжений, нормаль к которой составляет углы α, β, γ соответственно с σ1, σ2, σ3 определяются по формулам:
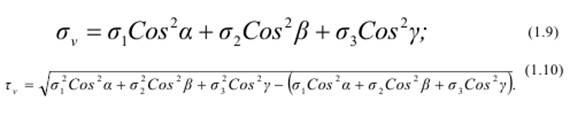
В случае плоского напряженного состояния формулы(1.1) – (1.10)упрощаются. Напряжения на наклонных площадках, если σz= 0, определяются из выражений
Угол наклона главных площадок определяется формулой
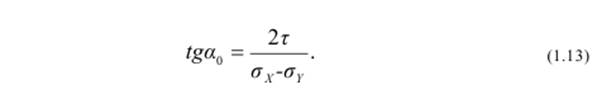
Значения главных (экстремальных) напряжений рассчитываются по выражению
Касательные напряжения на этих площадках равны нулю, что вытекает из формулы (1.12), и, следовательно, под углом α0 и α0+90º расположены главные площадки, и напряжения на них σmax и σmin являются главными напряжениями.
Наибольшие касательные напряжения действуют на площадках, наклонных под углом 45º к главным площадкам:
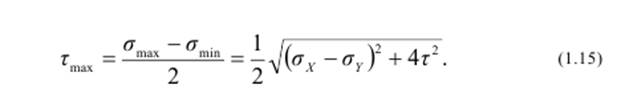
На площадках с максимальными касательными напряжениями действуют и нормальные напряжения, величина которых определяется полусуммой главных напряжений:
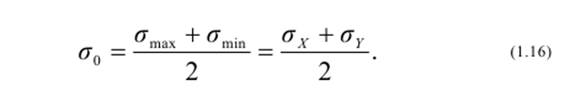
Относительные деформации определяются из обобщенного закона Гука
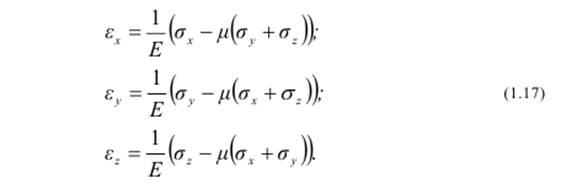
Относительное изменение объема можно определить по одной из возможных зависимостей
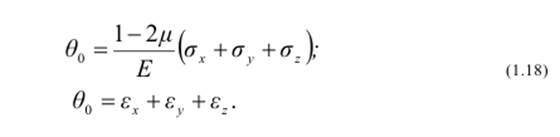
Удельная потенциальная энергия упругой деформации рассчитывается по формуле
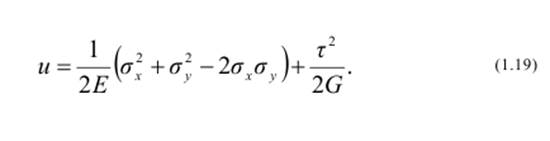
Аппаратура и материалы: линейка,карандаш,ручка,калькулятор длявыполнения инженерных расчетов, тетрадь.
Указания по технике безопасности
В помещении проведения лабораторных работ должно быть смешанное (естественное и искусственное) освещение, что обеспечивает освещенность в соответствии с требованиями к освещению учебных аудиторий.
В аудитории во время проведения занятий должна поддерживаться температура воздуха 20 ± 5 ºС, обеспечиваться работа вентиляции.
