Пример выполнения задания 2

Модуль 2

Решение иженерных задач средствами

Компьютерной математики

 

 

Лабораторная работа № 2

 

Нахождение корней нелинейных уравнений. Решение систем нелинейных уравнений

 

Цель: изучить основные возможности приложения Smath Studio для решения нелинейных уравнений и систем.

 

 

Вопросы для самоконтроля

1. Что является корнем уравнения?

2. Правило записи функции для использования команды solve.

3. В чем разница между численным и аналитическим нахождением корней уравнения?

4. Чем отличаются команды solve(2) и solve(4).

5. Для чего используется функция polyroots?

6. Правило записи вектора коэффициентов для polyroots.

7. Что является решение системы уравнений?

8. Правило записи уравнений для использования команды roots.

9. В чем разница между численным и аналитическим решениями системы уравнений?

10. Чем отличаются команды roots (2) и roots (3).

Индивидуальные задания 1

Найти корень уравнения численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

 

Таблица

№ варианта	Уравнение	№ варианта	Уравнение

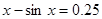
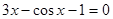
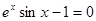
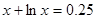
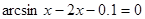
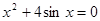
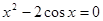
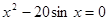
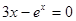
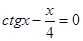
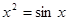
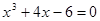
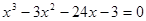
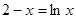
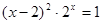
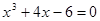
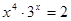
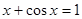
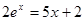
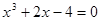
Индивидуальные задания 2

Найти численно корни полинома. Выполнить проверку.

Таблица

Вариант	Полином	Вариант		Полином
	x2-12x-4=0			x3-3x2-4x+1=0
	x3-24x+11=0			x3-34x2+4x+1=0
	x3+2x-7=0			x3-27x-17=0
	x3-21x+7=0			x4-2x3+2x2-2x+1=0
	x3-5x+1=0			x4-3x3+3x2-3x+2=0
	x3-12x+5=0			x4-3x3+5x2-3x+8=0
	x3+3x2-4x-1=0			x4-4x3+8x2-4x+16=0
	x3-9x2+20x-11=0			x4-4x3+4x2-4x+3=0
	x3-12x+5=0			x4-4x3+12x2-4x+27=0
	x3+6x2+6x-7=0			x4-6x3+18x2-6x+81=0
	x3-3x2-x+2=0			x4-5x3+10x2-5x+24=0
	x3-10x2+4x+9=0			x4-5x3+15x2-5x+54=0
	x4+x-1=0

Индивидуальные задания 3

Найти численное решение системы. Выполнить проверку.

 

Таблица

№ варианта	Система уравнений	Начальная точка
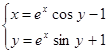
		(-0,9;1,4)
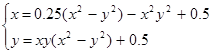
		(1;1)
		(1;1)
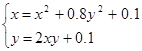
		(0;0)
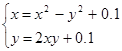
		(0;0)
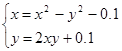
		(0;0)
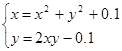
		(0;0)
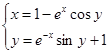
		(0,9;1,4)
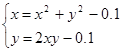
		(0;0)

Продолжение таблицы

№ варианта	Система уравнений	Начальная точка
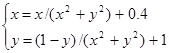
		(1;1)
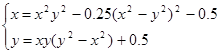
		(-0,5;0,5)
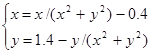
		(-1;1)
		(0;0)
		(0;0)
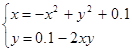
		(0;0)
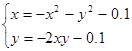
		(0;0)
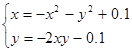
		(0;0)
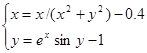
		(-1;1)
		(-0,9;-1,4)
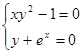
		(0,5;-1,5)
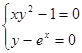
		(0,5;1,5)
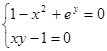
		(2;2)
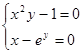
		(1,5;0,5)
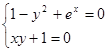
		(-2;2)
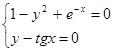
		(0;1)

Пример выполнения задания 1

 

Найти корень уравнения 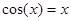численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

 

Методические рекомендации

Первый способ.

1. Запишите функцию (предварительно приведя уравнение к виду f(x)=0): .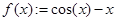

2. Постройте график функции. График пересекает ось абсцисс в одной точке, значит, уравнение имеет один корень.

3. Запишите стандартную команду:

solve(f(x); x)=.

Справа от знака равенства увидим результат: 0,7391.

2 Выполните проверку, найдя значение функции в полученной точке:

.

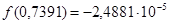Если бы решение было точным, то при проверке получили бы 0. Значение 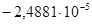означает, что результат получен с точностью до 4-го знака.

Конечный вид документа SMathStudio:

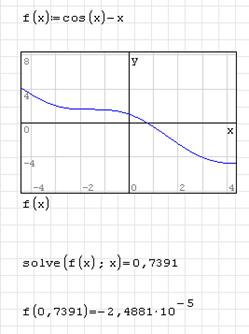
Второй способ.

1. Запишите функцию в виде: .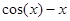

2 Выделите курсором переменную х.

3. В меню выбрать Вычисление ® Найти корни.

4. Выполните проверку.

1. Конечный вид документа SMathStudio:

 

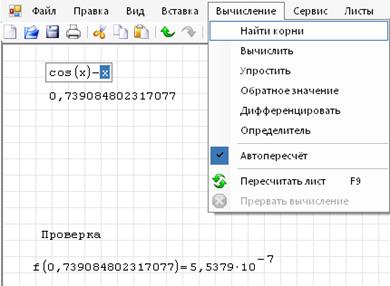
Третий способ.

1. Запишите функцию: .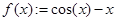

2. Для получения аналитического решения запишите стандартную команду:

solve(f(x); x), после которой на ПИ «Арифметика» выберите →.

3. Выполните проверку, найдя значение функции в полученной точке.

Конечный вид документа SMathStudio:

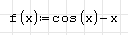
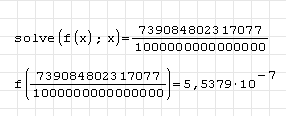
Если бы решение было точным, то при проверке получили бы 0. Значение 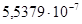означает, что результат получен с точностью до 4-го знака. Делаем вывод, что SMathStudio не может найти точные корни данного уравнения.

Примечание 1.

Если уравнение имеет несколько корней (как, например, уравнение 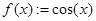), то применение стандартной процедуры решения даст ответ в виде вектора:

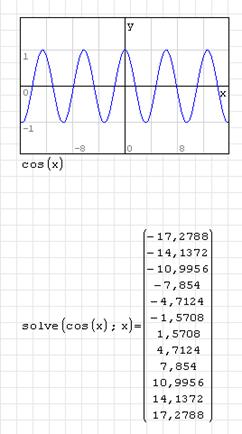
Корни выдаются в диапазоне «по умолчанию» [-20; 20]. Изменить диапазон можно в меню Сервис – Опции – Вычисление.

Можно использовать второй вариант этой процедуры для выбора решения на заданном промежутке. Для этого при наборе solve во всплывающей подсказке выбираем solve(4) и в шаблон вписываем:

Solve(<уравнение>; <имя переменной>; левая граница интервала; правая граница интервала). Получим:

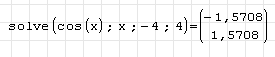
Примечание 2.

Если функция f(x) в уравнении f(x)=0 представляет собой полином степени n, то процедура solve может выдать только один корень. Чтобы получить все корни полинома (их количество совпадает со степенью полинома), стоит использовать встроенную функцию polyroots(v). Например, найдем численно корни полинома x³+2x-1=0.

1) задаем функцию (левую часть уравнения f(x)=0).

2) задаем вектор коэффициентов (кнопка на ПИ «Матрица»), в появившемся диалоговом окне указываем количество строк (равно степени полинома +1) и столбцов (количество уравнений).

3) записываем функцию polyroots(v)=.

4) делаем проверку, подставив найденные значения в функцию.

Конечный вид документа Smath Studio:

 

Пример выполнения задания 2

Решить систему уравнений 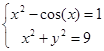численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.

 

Методические рекомендации

 

1. Записываем функцию roots(<уравнения>;<переменные>).

2. Для получения численного решения ставим знак «=». Получим результат с заданным количеством знаков после запятой.

3. Выполняем проверку, подставив полученные значения в исходную систему уравнений. В данном примере 1-ое уравнение решено точно, 2-ое – с точностью до 3-го знака.

4. Вид документа SMathStudio:

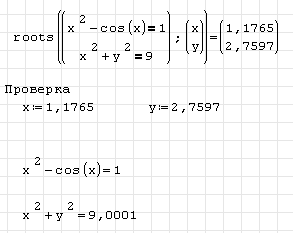
Можно каждое уравнение системы привести к виду f(x)=0. Тогда запись решения будет выглядеть следующим образом:

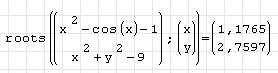
Если нужно получить одно из нескольких возможных решений, можно задать начальное приближение (координаты ближайшей известной к ответу точки) для переменных следующим образом: