Мостовые измерительные схемы

Методическое указание к лабораторной работе

Пенза-2016

Эффекты Зеебека и Пельтье

В 1821 году физик Т. Зеебек (1770-1831), родившийся в Эстонии, а учившийся в Германии, изучая тепловые эффекты в гальванических устройствах, соединил полукруглые элементы, изготовленные из висмута и меди. Неожиданно стрелки компаса, случайно лежавшего рядом, отклонились. Он проверил этот эффект на других соединениях металлов при разных температурах и обнаружил, что каждый раз получается различная напряженность магнитного поля. Однако, Зеебек не догадался, что при этом через элементы течет электрический ток, поэтому назвал это явление термомагнетизмом.

Если взять проводник, и один его конец поместить в холодное место, а другой – в теплое, от теплого участка к холодному будет передаваться тепловая энергия. Интенсивность теплового потока при этом пропорциональна теплопроводности проводника. В дополнение к этому градиент температур приводит к появлению в проводнике электрического поля, обусловлено эффектом Томсона (В. Томсон открыл этот эффект приблизительно в 1850 году. Он заключается в поглощении или высвобождении тепла линейно пропорционально току, проходящего через однородный проводник, имеющий градиент температуры вдоль его длины. При этом тепло поглощается, если ток и тепловой поток направлены в противоположных направлениях, и выделяется – когда они имеют одинаковое направление). Индуцированное электрическое поле приводит к появлению разности потенциалов:

где градиент температуры на небольшом участке длины , 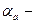абсолютный коэффициент Зеебека материала. Это уравнение является основным математическим выражением для термоэлектрического эффекта.

Что происходит, когда два проводника соединяются друг с другом? Свободные электроны в металле ведут себя как идеальный газ. Кинетическая энергия электронов определяется температурой материала. Однако в разных металлах энергия и плотность свободных электронов не являются одинаковыми. Когда два разных материала, находящихся при равной температуре, соприкасаются друг с другом, свободные электроны за счет диффузии перемещаются через место соединения. Электрический потенциал материала, принявшего электроны, становится более отрицательным, а материал, отдавший электроны, – более положительным. Разные концентрации электронов с двух сторон соединения формируют электрическое поле, уравновешивающее процесс диффузии, в результате чего устанавливается некоторое равновесие. Если контур является замкнутым, и оба соединения находятся при одинаковой температуре, электрические поля около них взаимно уничтожаются, чего не происходит, когда места соединений имеют разную температуру.

Последующие исследования показали, что эффект Зеебека является электрическим по своей природе. Можно утверждать, что термоэлектрические свойства проводников – это такие же объемные свойства материалов, как электро- и теплопроводность, а коэффициент 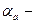уникальная характеристика материала. При комбинировании двух разных материалов всегда требуется определять напряжение Зеебека. Это можно сделать при помощи дифференциального коэффициента Зеебека:

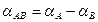Тогда напряжение на соединении равно:

Это уравнение иногда применяется для определения дифференциального коэффициента:

Например, функцию напряжения от градиента температуры для термопары Т-типа можно с достаточной степенью точности аппроксимировать при помощи уравнения второго порядка:

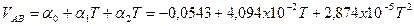Тогда выражение для дифференциального коэффициента Зеебека принимает следующий вид:

Из уравнения видно, что коэффициент является линейной функцией от температуры. Иногда он называется чувствительностью термопарного соединения. Эталонное соединение, которое, как правило, находится при более холодной температуре, называется, холодным спаем, а второе соединение – горячим спаем. Коэффициент Зеебека не зависит от физической природы соединения: металлы могут быть скручены, сварены, спаяны и т.д. Имеет значение только температура спаев и свойства металлов. Эффект Зеебека является прямым преобразованием тепловой энергии в электрическую.

Ниже приведены значения термоэлектрических коэффициентов и объемных удельных сопротивлений для некоторых типов материалов. Из соответствующей таблицы видно, что наилучшая чувствительность получается при соединении двух металлов, имеющих противоположные знаки коэффициентов 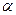при их максимально возможных значениях.

В 1826 году А. Беккерель предложил использовать эффект Зеебека для измерения температуры. Однако первая конструкция термопары была разработана Генри Ле-Шателье почти шестьюдесятью годами позже. Ему удалось обнаружить, что соединение проводов из платины и сплава платины и родия позволяет получить наибольшее термонапряжение. Ле-Шателье изучил и описал термоэлектрические свойства многих комбинаций металлов. Полученные им данные до сих пор используются при проведении температурных измерений. Выше приведены значения чувствительности некоторых наиболее распространенных типов термопар, соответствующие температуре 25 С, а на рисунке показаны напряжения Зеебека для стандартных термопар в широком температурном диапазоне.

Следует отметить, что термоэлектрическая чувствительность не является постоянной во всем интервале температур, и термопары обычно сравниваются при 0 С. Эффект Зеебека также используется в термоэлементах, которые, по существу, представляют собой несколько последовательно соединенных термопар. В настоящее время термоэлементы часто применяются для детектирования тепловых излучений. Первые термоэлементы, изготовленные из проводов, были разработаны Джеймсом Джоулем (1818-1889) для увеличения выходного напряжения измерительного устройства.

В настоящее время эффект Зеебека применяется в интегрированных датчиках, в которых соответствующие пары материалов наносятся на поверхность полупроводниковых подложек. Примером таких датчиков является термоэлемент для обнаружения тепловых излучений. Поскольку кремний обладает достаточно большим коэффициентом Зеебека, на его основе изготавливаются высокочувствительные термоэлектрические детекторы. Эффект Зеебека связан с температурной зависимостью энергии Ферми 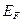поэтому коэффициент Зеебека для кремния n -типа можно аппроксимировать функцией от электрического удельного сопротивления в интересующем температурном диапазоне (для датчиков при комнатной температуре):

где Ом х м и являются константами, к – постоянная Больцмана, а электрический заряд. При помощи легирующих добавок получают материалы с коэффициентами Зеебека порядка 0,3…0,6 мВ/К. Выше приведены значения коэффициентов Зеебека для некоторых металлов и кремния. В таблице видно, что коэффициенты Зеебека для металлов гораздо меньше, чем для кремния, и что влияние алюминиевых выводов на микросхемы незначительное из-за высокого значения коэффициента Зеебека для кремния.

В начале девятнадцатого века французский часовщик, в последствии ставший физиком, Жан Шарль Атанас Пельтье (1785-1845) обнаружил, что при прохождении электрического тока из одного материала в другой, в месте их соединения происходит либо выделение, либо поглощение тепла, что зависит от направления тока:

где i - сила тока, а t – время. Коэффициент р имеет размерность напряжения и определяется термоэлектрическими свойствами материала. Следует отметить, что количество тепла не зависит от температуры других соединений.

Эффект Пельтье – это выделение или поглощение тепла при прохождении электрического тока через соединение двух различных металлов. Это явление характерно и для случаев, когда ток поступает от внешних источников, и когда он индуцируется в спае термопары из-за эффекта Зеебека.

Эффект Пельтье используется в двух ситуациях: когда надо либо подвести тепло к месту соединения материалов, либо отвести его, что осуществляется изменением направления тока. Это свойство нашло свое применение в устройствах, где где требуется осуществлять прецизионный контроль за температурой. Считается, что эффекты Пельтье и Зеебека имеют одинаковую природу. Однако следует хорошо понимать, что тепло Пельтье и Джоуля отличаются друг от друга. Тепло Пельтье в отличие от джоулева тепла линейно зависит от силы тока. (Тепло Джоуля выделяется при прохождении электрического тока любого направления через проводник, имеющий конечное сопротивление. Высвобождаемая при этом тепловая энергия пропорциональна квадрату тока: , где R – сопротивление проводника). Величина и направленность тепловой энергии Пельтье не зависит от физической природы соединения двух различных материалов, а полностью определяется их объемными термоэлектрическими свойствами. Эффект Пельтье используется для построения термоэлектрических охладителей, применяемых для снижения температуры детекторов, фотонов, работающих в дальнем ИК диапазоне спектра, а также охлаждаемых зеркальных гигрометров.

Термопары. Если соединить между собой два проводника из различны металлов, то при разных температурах спая и концов между последним возникнет разность потенциалов, за висящая от перепада температур и вида металлов спая. Чувствительность термопар характеризуется температурным коэффициентом ЭДС и принимает значения от 7.7 мкВ/К для термопар платина/родий 76 мкВ/К для термопар хромель/константан. Типовая схема включения термопары представлена на рисунке.

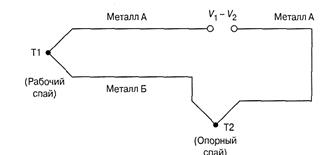
Типовая схема включения термопары

Пара металлов А и Б подобрана, исходя из требуемого температурного диапазона и максимальной чувствительности при приемлемой линейности. Наиболее распространены пары: железо-константан (тип J), хромель-алюмель (тип К), платина-платина/родий (типы S, R). Каждая пара изготавливается путем сварки (спайки) разных металлов. Рабочий спай помещается в зону измеряемой температуры, а опорный — в изотермальный блок, температура которого известна (в идеале равна 0°С). Напряжение выхода схемы зависит (почти пропорционально) от разности температур рабочего и опорного спаев. Обеспечить термостатирование опорного спая сравнительно сложно, поэтому чаще применяют схемы компенсации температуры опорного спая. Одна из таких схем приведена на рисунке.

Схема термокомпенсации опорного спая

Основная идея заключается в использовании полупроводникового датчика (на схеме ТМП-35), воспринимающего температуру опорного спая, и схемы, формирующей поправку к напряжению, т. е. компенсирующей разность между фактической температурой опорного спая и стандартной (0°С). Датчик ТМП-35, установленный на основании, изотермическом с опорным спаем, дает на выходе напряжение, пропорциональное температуре (10 мВ/°С). Это напряжение через делитель R ₁ R ₂компенсирует изменение термоЭДС опорного спая (-41 мкВ/°С). Резистор R₂ обеспечивает установку начального смещения шкалы. Выходное напряжение схемы пропорционально температуре рабочего спая 10 мВ/°С). Подробно интегральные полупроводниковые датчики температуры осмотрены ранее.

Фирма Analog Devices выпускает микросхемы AD594/5/6/7, представляющие

собой объединенные на одном кристалле измерительный усилитель и компенсатор температуры опорного спая. Опорные спаи формируются при припайке выводов термопары к расположенным в непосредственной близости друг от друга выводам микросхемы.

Резистивные термодатчики

Резистивные термодатчики (РТД) меняют свое сопротивление при изменении температуры. Они представляют собой помещенные в корпус катушечки с обмоткой из меди или иного металла или сплава с положительным температурным коэффициентом сопротивления МТКС). РТД имеют более высокую точность и линейность, чем термопары из тех же материалов. Особенно хороши, хотя и дороги, платиновые РТД. Они обладают прекрасной временной стабильностью. Рисунок иллюстрирует зависимость ТКС платинового РТД на 100 Ом и температурный коэффициент ЭДС (ТКЭ) платино-платинно/родиевой S-термопары.

Можно видеть, что ТКС РТД меняется относительно меньше, чем ТКЭ термопары, и это изменение линейно, что значительно облегчает его термокомпенсацию. Низкий ТКС платиновых РТД требует практически такого же усиления сигнала, что и от термопары. Резистивные термодатчики с большим сопротивлением имеют более высокую чувствительность, но, к сожалению, и большую инерционность.

Зависимость чувствительности платинового РТД и платино/ родиевой

S термопары от температуры

Мостовые измерительные схемы

Резистивные элементы широко используются в датчиках различного свойства и назначения. Это обусловлено их низкой ценой и простотой связи со схемами преобразования электрических сигналов. Резистивные элементы могут быть чувствительны к температуре, механическим деформациям, свету, магнитному полю и другим физическим воздействиям. С помощью резистивных датчиков измеряют вес, давление, влажность, скорость истечения газов и др. Резистивные датчики изготавливаются в зависимости от назначения и типа с сопротивлениями 50 Ом... 10 МОм. Например, характерное сопротивление тензодатчиков составляет 100, 200 Ом, термисторов — 3500 Ом и т. д.

Поскольку сопротивление этих датчиков зависит от физических величин, к которым они чувствительны, необходимо измерять их сопротивление и на основании характеристики преобразования определять значение соответствующей физической величины. Простейший способ измерения сопротивления состоит в пропускании через резистор стабильного тока I и измерении падения напряжения V. В этом случае

Точность измерения зависит от точности поддержания тока источника и точности измерения напряжения. Любые изменения тока могут быть восприняты как изменение сопротивления. К тому же температурные дрейфы, например, тензорезистора, также будут интерпретированы как изменение контролируемой деформации.

Применение мостовых схем позволяет во многом снизить остроту этих проблем. Основная схема моста Уинстона (фактически разработанного С. Кристи в 1833 году) показана на рисунке.

Мостовая измерительная схема (Мост Уинстона)

Основное уравнение моста имеет вид

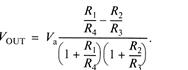
Условие баланса моста, т.е. когда 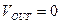, следующее

Оно не зависит от способа его возбуждения (от источника тока или источника напряжения, переменным или постоянным током), амплитуды возбуждения, сопротивления индикатора баланса.

Можно измерить сопротивление (например, r ₁) в плече моста компенсационным методом. Если, скажем, выбрать R₂ = R ₃, то, включив в качестве резистора R ₄ магазин сопротивлений, добиваются баланса моста. Тогда R ₁= R ₄. Компенсационный метод очень точен, но требует громоздкого прецизионного оборудования и плохо поддается автоматизации. Прямое измерение небаланса моста значительно проще.

На рисунке представлены мостовые схемы с различным включением датчиков (они показаны переменными резисторами) при питании постоянным напряжением (V_а = const),

Мостовые измерительные схемы с питанием от источника постоянного напряжения

а в таблице приведены функциональные зависимости для этих схем [2.7].

Таблица. Зависимость параметров мостовых схем с питанием от