Порядок выполнения работы. 1 Ознакомиться с устройством опор балок и их условным изображением

1 Ознакомиться с устройством опор балок и их условным изображением. В отчете начертить схему бал­ки и изобразить силы, приложенные к ней. Схема балки показана на рисунке 2.4. Силы выбираются по таблице 2.1 в соответствии с вариантом задания.

2 Вычислить величину и направление реакции опор балки.

3 Произвести экспериментальную проверку полученных результа­тов на установке, подобной указанной на рисунке 2.5.

3.1 Установить основание установки на неподвижную опору (стол, парта, верстак, подоконник…). При помощи регулировочных ножек 9 (рисунок 2.5) добиться горизонтального положения основания (контролировать уровнем).

3.2 На основание установить в требуемом (по заданию) положении опоры с измерительными устройствами 6 (электронные весы). На двутавровой балке разместить нагрузочные элементы 7, 8 и опоры 5 и 11, согласно задания. Установить балку на измерительные устройства, прикрепить нить динамометра 1 и сбросить показания «на ноль».

3.3 При помощи грузов приложить к балке заданную систему сил. Силы, направленные перпендикулярно оси балки, создаются грузи­ками, подвешенными на гибкой нити непосредственно к балке, а силы, направленные под углом, – нитями, перекинутыми через отклоняющий блок 9. Угол между нитью и осью балки определяется при помощи транспортира. Распределенная нагрузка создается размеще-нием соответствующих грузов на верхней полке балки. Количество грузиков для распределенной нагрузки определяется по формуле:

n = (q•l₅)/Q_n, (2.2)

где: q – распределенная нагрузка (по заданию), Н/м;

l₅ – длина действия распределенной нагрузки, м;

Q_n – вес одного грузика, Н.

При помощи грузов подвешенных непосредственно к нагрузочной пластине 8 и подвешенных через обводной блок 3 создается момент M. Вес грузиков (на одну нить) для создания момента определяется из формулы:

Q=M/l, (2.3)

где: M – момент по заданию, Н•м;

l – расстояние между приложенными силами, l = 0,05м.

3.4 Величина и направление реакции опор определяются по шкалам установки. Следует учесть, что на дисплее измерительных устройств 6, показания реакций в мм. Значения реакций опор в Ньютонах можно определить по формуле:

V_A(V_B) = m_A(m_B)•g/1000, (2.4)

где: m_A(m_B) – показания измерительных устройств, г;

g – ускорение свободного падения, 9,81м/с2.

3.5 Сравнить результаты, полученные опытным путем, с вычислен­ными по уравнениям равновесия.

 

Отчет о работе.

1 Номер варианта задания (по таблице 2.1).

Расчетная схема балки.

Данные: F₁ =...; F₂ =…; q =…; M =…; β =...; a =...; b =...; l₁ =…; l₂ =…; l₃ =…; l₄ =…; l₅ =…;.

2 Вычисление реакции опор НA; VA; VB. Полная величина реакции непо­движной опоры

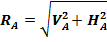, (2.5)

где: V_A и H_A – численное значение вертикальной и горизонтальной составляющих реакции R_{A .}Угол наклона

t_gβ_опыт=H_A/V_A; β_опыт =...

3 Опытное определение реакций опор:

V_Aопыт; V_Bопыт; β_{опыт .}

4 Сравнение результатов определения реакций, полученных теоретически и экспериментально.

5 Ответы на контрольные вопросы.

Контрольные вопросы

1 Сколько независимых уравнений равновесия можно составить для пло­ской системы параллельных сил?

2 Укажите, какие составляющие реакции опор балок возникают в подвиж­ной, неподвижной опорах и жесткой заделке.

3 Что такое распределенная нагрузка? Чем характеризуется?

4 Чем заменяется распределенная нагрузка при расчетах?

 

 

 

 

Рисунок 2.4 Рисунок 2.5

 

Таблица 2.1 Варианты задания

№ вар-а

Силы, Н

Распре- деленная нагрузка q, Н/м

Момент M, н•м

Длины участков, м

Угол β, град

F1

F2

a

b

l1

l2

l3

l4

l5

0,00 0,05 0,10 0,15 0,20 0,00 0,05 0,10 0,15 0,20 0,00 0,05 0,10 0,15 0,20 0,00 0,05 0,10 0,15 0,20 0,00 0,05 0,10 0,15 0,20 0,00 0,05 0,10 0,15 0,20

0,00 0,00 0,00 0,00 0,00 0,05 0,05 0,05 0,05 0,05 0,10 0,10 0,10 0,10 0,10 0,15 0,15 0,15 0,15 0,15 0,20 0,20 0,20 0,20 0,20 0,25 0,25 0,25 0,25 0,25

0,10 0,15 0,20 0,25 0,30 0,10 0,15 0,20 0,25 0,30 0,10 0,15 0,20 0,25 0,30 0,10 0,15 0,20 0,25 0,30 0,10 0,15 0,20 0,25 0,30 0,10 0,15 0,20 0,25 0,30

0,20 0,20 0,15 0,15 0,10 0,20 0,20 0,15 0,15 0,10 0,20 0,20 0,15 0,15 0,10 0,20 0,20 0,15 0,15 0,10 0,20 0,20 0,15 0,15 0,10 0,20 0,20 0,15 0,15 0,10

0,30 0,25 0,25 0,20 0,20 0,35 0,03 0,03 0,25 0,25 0,40 0,35 0,35 0,30 0,30 0,40 0,35 0,35 0,30 0,30 0,35 0,30 0,30 0,25 0,25 0,30 0,25 0,25 0,20 0,20

0,25 0,25 0,25 0,25 0,25 0,20 0,20 0,20 0,20 0,20 0,15 0,15 0,15 0,15 0,15 0,10 0,10 0,10 0,10 0,10 0,05 0,05 0,05 0,05 0,05 0,00 0,00 0,00 0,00 0,00

0,15 0,15 0,15 0,150,15 0,15 0,15 0,15 0,150,15 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25

 

 

Лабораторная работа №3

Проверка законов трения

Цель работы – ознакомиться с приближенными методами определения коэффициента трения скольжения; определить коэффициент трения скольжения различных материалов.

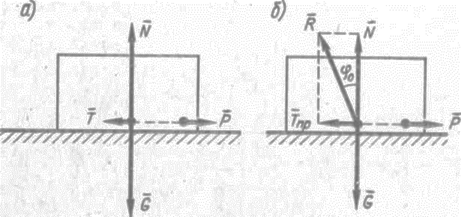
Рисунок 3.1

Теоретическое обоснование. При попытке сдвинуть одно тело относительно другого всегда обнаруживается, что между сухими твердыми телами возникает сила трения еще до начала движения. Это явление называется застоем.

При опоре одного тела силой тяжести G на другое (рисунок 3.1, а) кроме нормальной реакции N при действии сдвигающей силы Р возникает касательная реакция – сила трения Т.

С увеличением сдвигающей силы сила трения также возрастает и достигает предельной величины Т_пр (рисунок 3.1, б), затем с нача-лом движения сила трения несколько уменьшается. Сила трения всегда направлена в сторону, противоположную перемещению тела.

Трение представляет собой сложный комплекс механических (сдвиг, смятие выступов поверхности контакта), электрических и химических явлений. Величина силы трения скольжения зависит не только от материала, шероховатости поверхности, давления и относительной скорости скольжения, но и от целого ряда других причин: влажности, температуры и т. п. Учесть влияние всех фак­торов не представляется возможным, поэтому ограничиваются при­ближенным определением значения силы трения по закону Кулона: «Сила трения скольжения пропорциональна силе, нормальной к поверхности соприкасающихся тел, зависит от рода трущихся по­верхностей (их материала, обработки, смазки) и не зависит от величины площади трущихся поверхностей».

Отношение предельной силы трения к нормальной силе давле­ния называется статическим коэффициентом трения:

f₀ = T_пр /N, (3.1)

где: f₀ – безразмерная величина; T_пр [Н]; N [Н].

Сила трения отклоняет полную реакцию R (рисунок 3.1, б) от нормали на угол φ₀ – угол трения покоя. Тангенс угла трения покоя равен статическому коэффициенту трения:

tg φ₀ = T_пр /N= f₀, (3.2)

Отношение силы трения при движении к силе нормального давления называется динамическим коэффициентом трения сколь­жения. Он несколько меньше статического коэффициента трения скольжения.

Коэффициенты трения скольжения определяются опытным пу­тем различными способами. Наиболее часто эти коэффициенты для двух материалов (сталь по стали, чугун по стали, резина по стали и т.п.) определяются при помощи горизонтальной или наклонной плоскости.

Установка для определения коэффициента трения скольжения на горизонтальной плоскости. На рисунке 3.2 показана схема прибора для определения коэффициента трения скольжения, принцип действия которого следующий. Плоскость 1 при помощи винтов 6 устанавливается по уровню строго горизонтально (рисунок 3.2). К бруску 2 крючком 3 прикрепляется один конец шнура, перекинутого того через направляющий блок 4. К другому концу шнура привязана чаша 5. Блок 4 устанавливается таким образом, чтобы шнур от крючка до блока был параллелен плоскости 1. Чаша 5 пост пенно нагружается мелкими гирями, дробью или песком до тех пор, пока испытуемый образец 2 не начнет равномерно двигаться по плоскости.

Рисунок 3.2

На рисунке 3.3 изображен более сложный прибор для определения коэффициента трения скольжения на горизонтальной плоскости. Плита 1 перемещается равномерно вдоль направляющих станины. Эти движения плита получает от двигателя через червячный редуктор или вручную. Сила трения, возникающая на

Рисунок 3.3 поверхности контактов испытуемых материалов – плиты 1 и бруска 2, передается через тросик 3 на динамометр 5, закрепленный на стойке 4. Таким образом, этим прибором можно с гораздо большей точностью измерить величину силы трения, так как относительное движение создается принудительным равномерным перемещением одного из тел относительно другого.

Порядок выполнения работы по определению коэффициента трения скольжения на горизонтальной плоскости. Ознакомиться с устройством установки для определения коэффициента трения. В отчете по работе зарисовать принципиальную схему установки и показать силы, приложенные к образцу. Указать материалы, для которых определяются коэффициенты трения.

Подготовить образцы (бруски) и опорную плоскость плиты к испытанию, т.е. поверхность контакта протереть тряпочкой, смоченной в бензине и просушить. Образцы из резины, пластмассы и других материалов, реагирующих сбензином, протереть чистой сухой тряпочкой.

Определить силу тяжести испытуемых брусков и дополнительных грузов.

Установить и закрепить стойку на краю стола. На стойку закрепить диномометр.

К крючку испытуемого бруска привязать один конец шнура, к другому концу шнура прикрепить динамометр. Динамометр должен быть установлен так, чтобы шнур был направлен параллельно плоско­сти.

Плавно, равномерно потянуть за плиту, контролируя показания динамометра.

Опыт следует повторить не менее трех раз для каждого веса бруска. Результаты испытаний записать в таблицу 3.1отчета.

Вычислить величины коэффициентов трения.

Отчет о работе.

1 Схема установки и силы, приложенные к образцу.

G – сила тяжести бруска; Q₁ – сила тяжести чаши; Q₂ – сила тяжести груза; Р – движущая сила, направленная параллельно горизонтальной плоскости.

2 Таблица записей результатов испытания.

Таблица 3.1

Материал плиты…….	Материал бруска……
Сила тяжести бруска G, Н
а)…	б)…	в)…	г)…	д)...
Сила трения скольжения, определенная динамометром FТр, Н	1-й замер
2-й замер
3-й замер
Среднее значение
Движущая сила Р = FТр, Н
Статический коэффициент трения скольжения f0 = Р /G
Динамический коэффициент трения скольжения f = Р /G

3 Сравнить полученную величину коэффициента трения для данных пар материалов с величинами, указанными в справочной литературе.

4 Ответы на контрольные вопросы.

Установка для определения коэффициента трения скольжения на наклонной плоскости. Плоскость 1 при помощи винтового механизма 4 может быть установлена под различным углом к горизонтальной плоскости (рисунок 3.4). Величина угла наклона α отсчитывается по шкале 3. При увеличении угла наклона плоскости составляющая силы тяжести G₂, направленная парал-лельно наклонной плоскости, будет возрастать, соответственно будет увеличиваться и сила трения покоя Т.

При угле наклона плоскости, равном углу трения покоя (α = φ₀), сила трения достигнет предельной величины Т_пр. Приугле α > φ₀ образец 2 перейдет из состояния покоя в состояние дви­жения. Измерив угол α₀, равный углу трения φ₀, можно определить коэффициент трения покоя.

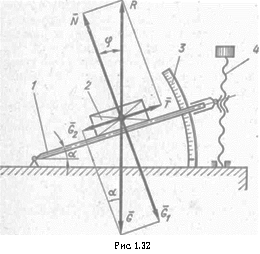Таким образом, коэффициент трения покоя f₀ численно равен тангенсу угла наклона плоскости, при котором тело под влиянием составляющей силы тяжести начнет движение:

f₀ = tg φ₀, (3.2)

При угле наклона плоскости больше угла трения (рисунок 3.5) (α>φ₀) тело, положенное на плоскость, начнет двигаться равно­ускоренно и за время t пройдет путь S. Динамический коэффициент трения при равноускоренном движении оп­ределяется по формуле

Рисунок 3.4 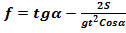, (3.3)

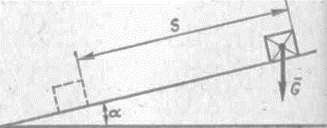где: α – град; S – м; t – с; g = 9,81м/с² – ускорение свобод­ного падения.

Наибольшую трудность при этом способе измерения коэффи-циента трения движения, вызывает точное нахождение времени движения, которое определяется по секундомеру, включаемому вручную. Рисунок 3.5