Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Существует три способа построения развертки многогранных поверхностей:
1. Способ нормального сечения;
2. Способ раскатки;
3. Способ треугольника.
Пример 1. Развертка пирамиды
При построении развертки пирамида применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.
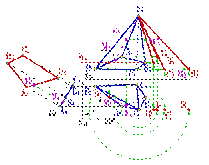
Алгоритм построения можно сформулировать следующим образом (рис.):
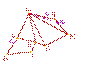1.Определяют натуральную величину основания пирамиды (например методом замены плоскостей проекций);
2.Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);
3.Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рис.).
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки.
Примером первой точки на рисунках служит точка К 0 и К О SАD, а иллюстрацией второго случая являются точки М 0 и М 0*. Для определения точки К 0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ (метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S 0 М 0 и, наконец, точки К 0.
Пример 2. Развертка призмы
В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.
Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения – треугольника 1, 2, 3, а затем определяют истинную величину этого сечения. На примере она найдена методом вращения.
В дальнейшем строям отрезок 10-10*, равный периметру нормального сечения. Через точки 10, 20, 30 и 10* проводят прямые, перпендикулярные 10-10*, на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 1 0 D 0= 1 4 D 4 и 1 0 А 0= 1 4 А 4.
Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание.
