Цель: выявить статистические закономерности модификационной изменчивости количественных признаков.
Модификационная изменчивость – массовое явление: изменения наблюдаются не у одного организма, а у группы. Всю группу объектов, которая подлежит изучению, называют генеральной совокупностью. Часто бывает затруднительно или вообще невозможно ее изучить. В таком случае изучают часть особей – выборочную совокупность, на основании которой дают общую характеристику. Выборку необходимо брать из однородного материала и без специального отбора, так чтобы она отражала генеральную совокупность.
В зависимости от характера варьируемого признака модификационная изменчивость бывает качественной и количественной. При качественной изменчивости разница между объектами выражается качественным показателем, который у одних объектов присутствует, а у других нет. Например, пыльцевые зерна жизнеспособны (фертильны) и нежизнеспособны (стерильны), растения болеют определенной болезнью или нет, и т. д. Количество объектов с определенной качественной оценкой обычно выражается в процентах. Количественная изменчивость характеризуется степенью выраженности признака. Она подразделяется на прерывистую (дискретную) и непрерывную. В первом случае признаки выражаются в целых абстрактных числах, между которыми нет переходов (количество листьев на растении, количество колосков в колосе и т. д.). Во втором случае варьируемые признаки измеряются единицами, между которыми возможны переходы (масса, длина, толщина и т. д.).
Объективную характеристику количественной изменчивости можно дать лишь при использовании статистического метода исследования: составления вариационного ряда и обработки его параметров.
Отдельное значение признака, который варьирует, в вариационной статистике принято называть варианта (ее обычно обозначают буквой х). Число, которое обозначает, сколько раз повторяется варианта, называется частотой встречаемости варианты – р. Число особей, входящих в исследуемую группу (объем совокупности), обозначают через п. Совокупность может быть представлена как ряд вариант: х1; х2 х3, х4.... хn.... где х – любая варианта; х n – последняя варианта.
Минимальная (хmin) и максимальная (хmax) варианты совокупности служат пределами вариации.
Расположение вариант совокупности по степени возрастания или убывания признака, от х min до хmax или наоборот, составляет вариационный ряд. Например, при изучении числа лопастей листьев дуба получены следующие первичные данные: 7, 8, 12, 10, 9, 13, 11, 12, 8, 10, 15 и т. д. Если определить наименьшую и наибольшую варианты и распределить все варианты в возрастающем порядке (от наименьшей к наибольшей), получим вариационный ряд, который будет иметь вид: 7, 8, 9, 10, 11, 12, 13,1 5 и т. д.
При непрерывной изменчивости вариации число вариант в совокупности может оказаться значительным. В таком случае их для удобства группируют в классы с учетом величины классового интервала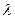 
, которую устанавливают по формуле:
= 
,
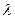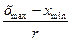где r – число классов (при объеме совокупности 25–60 вариант ее обычно делят на 5–8 классов; 60–100 – 7–10 классов).
Например, длина колоса пшеницы сорта «Мироновская 808» варьирует в пределах 70–112 мм. В этом случае совокупность удобно разделить на 7 классов: 112 мм – 70 мм = 42 мм; 42 мм: 7 = 6 мм (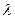 = 6 мм).
Группировка по классам и составление вариационного ряда при непрерывной изменчивости ведется так, чтобы начало каждого последующего класса отличалось от предыдущего на величину классового интервала, например: 70– 75 мм; 76–81 мм; 82–87 мм; 88–93 мм и т. д. (при 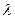= 6). Затем намечают границы классов, находят средины классов и составляют непрерывный ряд. Вариационный ряд можно изобразить графически, т. е. в виде диаграммы, или в виде кривой распределения особей в совокупности в зависимости от степени выраженности признака (вариационная кривая).
При построении диаграммы на оси абсцисс откладывают границы классов, а на оси ординат – частоту встречаемости вариант в данном классе. Например, для изменения длины колоса пшеницы диаграмма будет иметь вид:
70 
 |
10 20 30 40 50 60
При построении вариационной кривой на оси абсцисс откладывают средние значения классов (или варианты), а на оси ординат – частоту встречаемости вариант.
Например, если при изучении изменчивости числа лопастей листьев дуба были получены следующие значения х и р (при п = 100);
| х | ||||||||
| р |
вариационная кривая будет иметь вид:
Основные показатели ряда варьируемого признака – средняя арифметическая х и среднее квадратичное отклонение σ. Средняя арифметическая определяется по формуле:
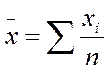
Средняя арифметическая дает общее представление о группе объектов, но она не раскрывает степени варьирования изучаемого признака. Средние арифметические могут быть одинаковыми для двух групп объектов в том случае, когда между ними есть существенная разница. Например, среднее число зерновок в колосе сорта А – 33,5 и сорта Б – 33,5. Первое значение получено из данных, варьировавших в пределах от 29 до 39, а второе – из данных, которые варьировали в пределах от 25 до 45. Таким образом, средней арифметической недостаточно для характеристики совокупности, поскольку ее главной особенностью является разнообразие членов.
Для определения изменчивости совокупности можно использовать вариационный размах, т. е. разницу между максимальной и минимальной вариантами. Но данная величина непостоянна и с увеличением объема выборки может изменяться. Поэтому необходим показатель, с помощью которого можно было бы обобщить изменчивость всех вариант. Таким показателем является среднее квадратичное отклонение, которое вычисляется по формуле:
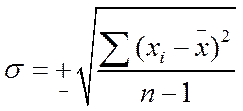
где σ – число, показывающее, на какую величину каждая варианта совокупности отличается от х.
Любой признак при варьировании практически отклоняется от средней арифметической в основном не более чем на Зσ. Поэтому тройное значение квадратичного отклонения принято считать крайней ошибкой отдельного наблюдения. Шестикратное значение сигмы (от Зσ до –Зσ) есть амплитуда колебания признака. С помощью х и σ рассчитывают другие статистические величины – коэффициент вариации и ошибку средней арифметической.
Ход работы
1. Изучите предложенные объекты одного вида. Измерьте их величину или число каких–либо деталей строения, массу, длину органа и т. п. у 25 экземпляров предложенного объекта (один объект изучает группа студентов из 4 человек). Полученные данные занесите в таблицу:
_________________________________________________
2. Совместно с другими участниками группы, изучающей такой же признак, выявите минимальное и максимальное значение измеряемого признака, определите размах его изменчивости (из максимального значения вычитают минимальное).
Размах изменчивости признака: ____________________
Разделите полученную величину на 10, чтобы получить классы величин для разноски полученных данных.
Величина классового интервала равна: ______________
Определите границы 10 классов. Составьте вариационный ряд. Данные запишите в таблицу.
Данные для вариационного ряда
| Номера классов | Границы классов | Число (сколько раз встретились варианты, попавшие в границы каждого класса) | ||
| Данные собственных измерений | Данные других участников группы | Суммарные данные | ||
| 1. 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. |
3. Изобразите полученный вариационный ряд в виде диаграммы или вариационной кривой.
4. Сделайте вывод о распределении особей по данному признаку в выборке (каких особей в выборке больше, а каких меньше).
Вывод_________________________________________________
_____________________________________________________
4. Вычислите среднюю арифметическую изучаемого признака.
5. Вычислите среднее квадратичное отклонение. Для облегчения вычислений используйте вспомогательную таблицу.
| Варианты, х | Отклонения, х – х | Квадраты отклонения, (х – х)2 |
Сумма квадратов отклонения для показателей всей группы:
S (х – х)2 = ;
σ = ;
6. Для сравнения разнообразия признаков в различных вариационных рядах пользуются коэффициентом вариации, который вычисляется по формуле:
σ ´ 100
с= ––––––––––.
х
Определите коэффициент вариации для составленного вашей группой вариационного ряда:
с=––––––––––––––.
Контрольные вопросы
1. Что такое пределы модификационной изменчивости? Приведите примеры собственных наблюдений за проявлением модификационной изменчивости растений и животных.
2. Почему наиболее часто встречаются особи со средней степенью выраженности признака?
3. В каких областях человеческой деятельности важно знание нормы реакции организма? Ответ подтвердите примерами.
4. Каковы возможные причины мутаций?
5. Перечислите основные группы мутагенных факторов. Приведите примеры.
6. Что такое генные мутации? Приведите примеры.
7. Что такое геномные мутации?
8. Выпишите хромосомный набор:
а) нуллисомиков:
б) моносомиков:
в) полисомиков:
г) трисомиков:
9. Чем опасны близкородственные браки?
