НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Рабочая тетрадь

Новосибирск 2012
УДК Кафедра теоретической и
ББК прикладной механики
Н
Авторы: доц. Т.В. Семенова,
ст. преп. Е.В. Петрова
Рецензент канд. тех. наук, доц. С.Г. Щукин
Начертательная геометрия: Рабочая тетрадь / Новосиб. гос. аграр. ун-т; Сост.: Т.В. Семенова, Е.В. Петрова – Новосибирск, 2012. – с. 96
Рабочая тетрадь окажет помощь студентам при подготовке к практическим занятиям, программированному контролю знаний и экзамену. Данная разработка экономит лекционное время на конспектировании учебного материала, приведенного в данном пособии. Наличие рабочей тетради по предмету на лекционных и практических занятиях является обязательным требованием, предъявляемым преподавателем к студенту.
Рабочая тетрадь с решенными задачами является допуском к экзамену или основанием для получения зачета и допуском к экзамену.
Предназначена для студентов Инженерного института направлений подготовки: Профессиональное обучение (агроинженерия),Агроинженерия, Эксплуатация транспортно-технологических машин и комплексов, Технология транспортных процессов.
Курс лекций утвержден и рекомендован к изданию методическим советом Инженерного института (протокол №…. от ………2012 г.).
© Новосибирский государственный аграрный университет, 2012
ВВЕДЕНИЕ
Методическая разработка предназначена для одновременного использования как в качестве сборника задач и контрольных вопросов, так и в форме рабочей тетради.
Решения задач в настоящей рабочей тетради выполняются непосредственно на заданной печатной основе их графических условий. Рабочая тетрадь служит необходимым дополнением к курсу лекций Т.В. Семеновой, Е.В. Петровой «Начертательная геометрия», размещенному, как и тетрадь на сайте Инженерного института (http://mechfac.ru/). В соответствии с курсом лекций содержание материала тетради разбито на девять основных базовых тем. В начале каждой темы даются краткие теоретические пояснения, затем следуют базовые задачи, а в конце темы вопросы для самопроверки.
Часть задач, представленных в рабочей тетради, решается на практических занятиях совместно с преподавателем, остальные задачи выполняются в качестве домашней, индивидуальной и самостоятельной работы. Рабочая тетрадь с необходимым количеством решенных задач и ответами на вопросы для самоподготовки является допуском к сдаче экзамена.
Правильность и качество решения задач во многом зависит от аккуратности и точности графических построений. Все построения в тетради необходимо выполнять с помощью чертежных инструментов (циркуль, угольник, транспортир). На чертеже должны быть сохранены все вспомогательные построения, выполнены все необходимые обозначения в соответствии с принятыми требованиями. Вспомогательные построения выполняются сплошными тонкими линиями остро заточенным карандашом. Линии видимого контура обводятся сплошными толстыми основными линиями мягким карандашом. Линии невидимого контура выполняются тонкими штриховыми линиями. Геометрический элемент, который требовалось найти, построить, определить по условию задачи рекомендуется выделять цветным карандашом или цветной ручкой.
ОБОЗНАЧЕНИЯ И СИМВОЛЫ
| Обозначения геометрических фигур в различных системах | |||

| 
| 
| |
| ■ Фигура | Ф | Ф | Ф |
| ■ Плоскости проекций: - горизонтальная - фронтальная - профильная | Н V W | Н V W | П1 П2 П3 |
| ■ Точки в пространстве | A, B, C | ||
| ■ Проекции точек: - горизонтальная - фронтальная - профильная | а, в, с а/, в/, с/ а//, в//, с// | А/, B/, C/ A//, B//, C// A///, B///, C/// | А1, В1, С1 A2, B2, C2 A3, B3, C3 |
| ■ Линии | двумя точками | ||
| ■ Проекции линий | проекциями точек | ||
| ■ Плоскости | P, Q, S, a, b, g | ||
| ■ Следы плоскостей: - горизонтальные - фронтальные - профильные | Pн,Qн, Sн PV, QV, SV PW, QW,SW | aн, bн, gн aV, bV, gV a W, b W, g W | aп1, bп1,gп1 aп2, bп2,gп2 aп3,bп3, gп3 |
| Символы, обозначающие отношения между геометрическими фигурами: | |||
| - совпадение, результат действия - конгруэнтность - перпендикулярность - объединение - пересечение - включает - принадлежит, является элементом - конъюкция предложений, союз И - квантор общности - логическое следствие | = @ ^ È Ç Ì Î Ù " Þ |
ГОСТ 2.303-68*. Линии (выписки)
Таблица 1 – Типы линий и их назначение

Окончание таблицы Б.1
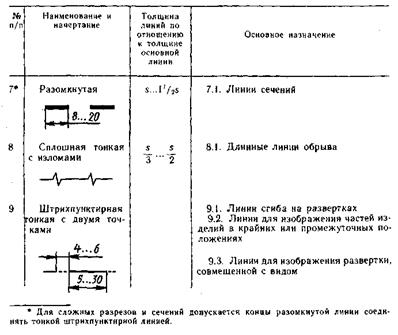
Линия – основной элемент графики. В табл. 1 представлены наименования, начертания и назначения линий на чертежах всех отраслей промышленности, архитектуры и строительства в соответствии с требованиями Государственных стандартов – ГОСТ 2.303-68. Их называют стандартными чертежными линиями. Они широко применяются в графике инженерами и техниками в процессе технического проектирования и конструирования. Вы в своих графических работах и в рабочей теради будете использовать эти линии.





|

Задание. По выписке из ГОСТ 2.304-81 напишите русский алфавит прописными и строчными буквами, а также цифры и специальные знаки, свою фамилию, имя, наименование вуза, номер группы..


ТЕМА 2
Комплексный чертеж (эпюр) точки состоит из двух или трех ортогональных проекций. Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из плоскостей проекций H - называется горизонтальной плоскостью проекций, вторая V - фронтальной, а третья W - профильной. Линии пересечения плоскостей проекций называются осями координат x, y, z.
Плоскости проекций делят пространство на 8 трехгранных углов - четверти или октанты. Система знаков соответствует "правой системе" координат, принятой в большинстве европейских стран. Зритель, рассматривающий оригинал, находится в первом октанте.
Две проекции одной и той же точки лежат на одной линии связи, которая перпендикулярна оси проекций. Положение точки на плоскости определяется двумя координатами. Координата – отрезок, выражающий расстояние точки до плоскости проекций. Две проекции точки определяют ее положение в пространстве. По двум проекциям точки можно определить все три ее координаты.
На комплексных чертежах, как правило, не ограничивают плоскости проекций, и положение их задают осями. В тех случаях, когда условиями задачи этого не требуется, проекции точек могут быть даны без изображения осей. Такая система называется безосной.
Прямая линия в пространстве определяется положением двух ее точек. Значит, достаточно выполнить комплексный чертеж этих точек, а затем соединить одноименные проекции точек прямыми линиями, чтобы получить соответственно горизонтальную и фронтальную проекции прямой.
Длину отрезка прямой по его проекциям определяют как гипотенузу прямоугольного треугольника, одним катетом которого является одна из проекций данного отрезка, а другим катетом – абсолютная величина алгебраической разности расстояний от концов другой проекции отрезка до оси проекций.
Угол в треугольнике между катетом – горизонтальной проекцией отрезка – и гипотенузой – его действительной величиной – равен углу наклона самого отрезка к горизонтальной плоскости проекций (угол a).
Угол в треугольнике между катетом – фронтальной проекцией отрезка – и гипотенузой – его действительной величиной – равен углу наклона самого отрезка к фронтальной плоскости проекций при построении прямоугольного треугольника на фронтальной плоскости проекций.
Следами прямой называют точки (M, N) ее пересечения с плоскостями проекций.
Горизонтальным следом прямой называют точку ее пересечения с горизонтальной плоскостью проекций. Горизонтальный след прямой обычно обозначают буквой М, а его проекции буквами (m, m/).
Фронтальным следом прямой называют точку ее пересечения с фронтальной плоскостью проекций. Фронтальный след прямой обычно обозначают буквой N, а его проекции буквами(n, n/).
 Задача № 1. Построить проекции точек по заданным координатам: А (20, 35, 15), В (45, 15, 35)
Задача № 1. Построить проекции точек по заданным координатам: А (20, 35, 15), В (45, 15, 35)

 Задача № 2. По двум заданным проекциям отрезка АВ построить его третью проекцию
Задача № 2. По двум заданным проекциям отрезка АВ построить его третью проекцию


Задача № 3. Построить проекции отрезка прямой DE по заданным координатам его концов D (10, 5, 35), Е (45, 25, 10). Дайте наглядное изображение этого отрезка.

Задача № 4. Определить натуральную величину отрезка АВ способом прямоугольного треугольника. Укажите углы наклона прямой к плоскостям проекций.
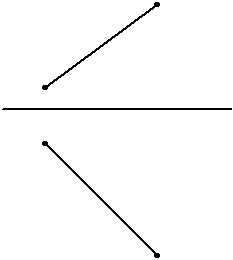
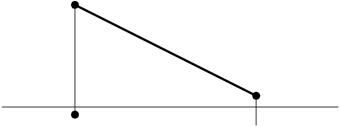
Задача № 5. Построить горизонтальную проекцию восходящего отрезка АВ, если известно, что угол наклона его к плоскости V составляет 30˚.
Вопросы для самоподготовки
1. Как обеспечивается на эпюре условие обратимости чертежа точки?
2. Какие координаты точки однозначно определяют ее положение в пространстве?
3. Как располагают профильную плоскость проекций? Как строят профильную проекцию точки?
4. Что такое безосный эпюр и когда целесообразно его применение?
5. Какие знаки имеют координаты Z точек, расположенных под горизонтальной плоскостью проекций? Какие знаки имеют координаты Y точек, расположенных за фронтальной плоскостью проекций?
6. Как расположены точки, у которых:
а) Y = 0;
б) Z = 0;
в) Y = Z = 0?
7. Как определить, в какой четверти пространства лежит точка, если даны:
а) эпюр точки;
б) координаты точки?
8. Когда для точки А возможен случай:
а) а/ = а;
б) а/ = а = а//?
9. Какое положение может занимать точка относительно основных плоскостей проекций? В чем отличие точек общего положения от точек частного положения?
Задачи:
1. На заданном наглядном изображении (прямоугольная изометрическая проекция) обозначить геометрические элементы аппарата проецирования точки А на две плоскости проекций, записать в таблицу их обозначения и названия.
Построить эпюр точки А, соответствующий наглядному изображению, и записать в таблицу обозначения и названия того элемента эпюра, который соответствует на наглядном изображении (и в пространстве).



 2. По заданному наглядному чертежу построить эпюры точек и записать их координаты в таблицу.
2. По заданному наглядному чертежу построить эпюры точек и записать их координаты в таблицу.

ТЕМА 3
Прямая в пространстве может занимать как общее, так и частное положения. Прямая общего положения – прямая наклоненная ко всем плоскостям проекций. Прямые частного положения могут занимать положения параллельные плоскостям проекций и перпендикулярные плоскостям проекций.
Прямые параллельные плоскостям проекций называются прямыми уровня. Прямая параллельная плоскости Н называется горизонталью, прямая параллельная плоскости V - фронталь, прямая параллельная W – профильная прямая.
Прямая перпендикулярная горизонтальной плоскости проекций (горизонтально-проецирующая прямая) на чертеже горизонтальная проекция прямой - точка, а фронтальная ее проекция – прямая, перпендикулярная к оси Х.
Прямая перпендикулярная фронтальной плоскости проекций (фронтально-проецирующая прямая) на чертеже фронтальная проекция прямой - точка, а горизонтальная ее проекция – прямая, перпендикулярная к оси Х.
Прямая перпендикулярная профильной плоскости проекций (профильно-проецирующая прямая) на чертеже фронтальная и горизонтальная проекции прямой – линии параллельные оси Х, а профильная ее проекция – точка.
Если в пространстве прямые пересекаются, то на эпюре одноименные проекции прямых пересекаются и точки их пересечения лежат на одной линии связи. В частном случае пересекающиеся прямые могут быть перпендикулярны между собой.
Любой угол, стороны которого расположены параллельно плоскости проекций, проектируется на эту плоскость без искажения.
Прямой угол, у которого хотя бы только одна сторона параллельна плоскости проекций, проектируется на эту плоскость тоже прямым углом (т. е. без искажения). Таким образом, если в пространстве даны две взаимно перпендикулярные пересекающиеся прямые, одна из которых расположена параллельно плоскости проекций, то их проекции на этой плоскости тоже будут взаимно перпендикулярны.
Если прямые в пространстве параллельны на эпюре одноименные проекции прямых параллельны.
Если прямые не пересекаются и не параллельны, то они скрещиваются.
Взаимное расположение двух прямых при наличии хотя бы одной профильной прямой устанавливается по третьей проекции.
Задача № 6. Определить взаимное расположение прямых CD и EF.

Задача № 7. Определить расстояние от точки С до прямой АВ.

Вопросы для самоподготовки
1. Какие случаи взаимного расположения прямых возможны? Как по эпюру определить характер взаимного расположения двух прямых?
2. Как используется теорема о проецировании прямого угла при построении взаимно перпендикулярных прямых на эпюре?
3. Какие проекции прямых уровня относят к главным и почему?
4. Какие прямые считают восходящими, а какие - нисходящими?
5. Как используется при чтении эпюра теорема, обратная теореме о проецировании прямого угла?
6. Перечислите способы задания прямой в пространстве. Приведите графические примеры.
7. Какие метрические задачи можно решать без дополнительных построений на эпюрах прямых частного положения?
Задачи
1. Определить и записать, какое положение занимает каждое звено схематизированного трубопровода. Сделать проволочную модель ломаной АВС…М.
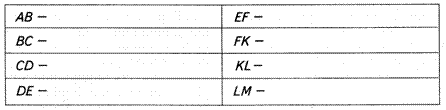

2. а) Определить, как расположена в пространстве прямая а относительно основных плоскостей проекций и смоделировать ее.
б) Найти проекции следов заданной прямой на основных плоскостях проекций.
в) Построить профильную проекцию прямой.
г) Построить наглядное изображение прямой а и проекции.


3. Определить углы наклона заданных прямых к основным плоскостям проекций
 4. Построить проекции точек С и Е, расположенных так, что: |АС|: |СВ| = 1: 3; |КЕ|: |КL| = 2: 1; С Î АВ; Е Î КL.
4. Построить проекции точек С и Е, расположенных так, что: |АС|: |СВ| = 1: 3; |КЕ|: |КL| = 2: 1; С Î АВ; Е Î КL.

 5. Определить и записать, как расположены относительно друг друга прямые а и b.
5. Определить и записать, как расположены относительно друг друга прямые а и b.

6. а) Определить взаимное расположение прямых а и b.
б) Показать на эпюре видимость проекций прямых с и d в окрестностях конкурирующих точек.
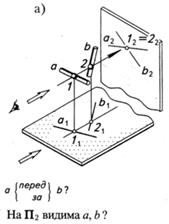

7. Определить и записать, на каких чертежах показаны взаимно перпендикулярные прямые.


8. Указать в таблице обозначения соответствующих линий поверхности резца.



ТЕМА 4
Плоскость может быть задана в пространстве следующими геометрическими элементами: тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на этой прямой; двумя параллельными прямыми; двумя пересекающими прямыми; плоской фигурой; следами плоскости.
Следом плоскости называется линия, по которой данная плоскость пересекается с плоскостью проекций. Общую точку следов плоскости называют точкой схода следов плоскости. Например, для плоскости Р: Рн – горизонтальный след плоскости – линия пересечения плоскости Р с горизонтальной плоскостью проекций. Рv – фронтальный след плоскости – линия пересечения плоскости Р с фронтальной плоскостью проекций Рw – профильный след плоскости – линия пересечения плоскости Р с профильной плоскостью проекций.
Плоскость, произвольно наклоненную к плоскостям проекций, называют плоскостью общего положения.
Плоскость, перпендикулярную к горизонтальной плоскости проекций, называют горизонтально-проецирующей плоскостью.
Плоскость, перпендикулярную к фронтальной плоскости проекций, называют фронтально-проецирующей плоскостью.
Плоскость, перпендикулярную к профильной плоскости проекций, называют профильно-проецирующей плоскостью.
Плоскость, параллельную горизонтальной плоскости проекций, называют горизонтальной уровня (ее фронтальный след параллелен оси Х).
Плоскость, параллельную фронтальной плоскости проекций, называют фронтальной уровня (ее горизонтальный след параллелен оси Х).
Плоскость, параллельную профильной плоскости проекций, называют профильной уровня (ее фронтальный и горизонтальный следы параллельны осям Z и Y).
Точка, взятая на какой-либо из прямых, определяющих плоскость, принадлежит плоскости или точка принадлежит плоскости, если через нее можно провести прямую, лежащую в плоскости.
Прямая принадлежит плоскости, если она имеет с плоскостью две общие точки.
Горизонталью плоскости называют прямую, лежащую в этой плоскости и параллельную горизонтальной плоскости проекций.
Фронталью плоскости называют прямую, лежащую в плоскости и параллельную фронтальной плоскости проекций.
Линией наибольшего ската плоскости называют лежащую в этой плоскости прямую, которая перпендикулярна произвольной горизонтали плоскости.
Для того чтобы найти точку пересечения прямой с плоскостью, поступают так:
1. заданную прямую заключают в произвольную вспомогательную плоскость, как правило, проецирующую;
2. находят прямую пересечения плоскостей – заданной и вспомогательной;
3. на пересечении прямых – заданной и полученной – получается искомая точка;
4. определяется видимость участков прямой (заданной) с помощью конкурирующих точек (с помощью фронтально конкурирующих точек определена видимость на фронтальной плоскости проекций, а с помощью горизонтально конкурирующих точек – на горизонтальной плоскости проекций).
Прямая параллельная прямой, лежащей в плоскости параллельна и этой плоскости.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
У параллельных плоскостей соответствующие следы параллельны.
Прямая перпендикулярная к плоскости должна быть перпендикулярна двум пересекающимся прямым этой плоскости. За две пересекающиеся прямые берутся горизонталь и фронталь плоскости, поэтому горизонтальная проекция прямой перпендикулярной плоскости перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная ее проекция перпендикулярна фронтальной проекции фронтали этой плоскости. Проекции прямой перпендикулярной к плоскости перпендикулярны соответствующим следам этой плоскости.
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости.
Задача № 8. Через прямую DK провести фронтально-проецирующую плоскость P, а через прямую АВ – горизонтально-проецирующую плоскость Q. Найти следы плоскостей.
 а) б)
а) б)
Задача № 9. Построить недостающую проекцию точки К, принадлежащую плоскости треугольника АВС.

Задача № 10. Провести в плоскости треугольника АВС горизонталь, а в плоскости треугольника EDK – фронталь.
а) б)

Задача № 11. Определить горизонтальную проекцию плоского пятиугольника ABCDE, зная вертикальную его проекцию и горизонтальную проекцию двух смежных сторон.

Задача № 12. Построить проекции линии пересечения плоскостей и определить их видимость.
а) б)

Задача № 13. Построить проекции точек пересечения прямой АВ с плоскостью Р и определить видимость участков прямой.
а) б)

Задача № 14. Построить проекции точек пересечения прямой с плоскостью треугольника, установить видимость участков прямой.
а) прямой DE с ΔАВС:
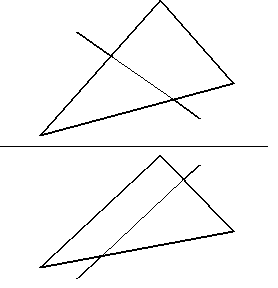
б) прямой АВ с ΔEDK:

Задача № 15. Из вершины А треугольника АВС восстановить перпендикуляр L длинной 30 мм.

Задача № 16. Построить проекции линии пересечения двух треугольников и определить их видимость.
а) по точкам пересечения прямых линий с плоскостью
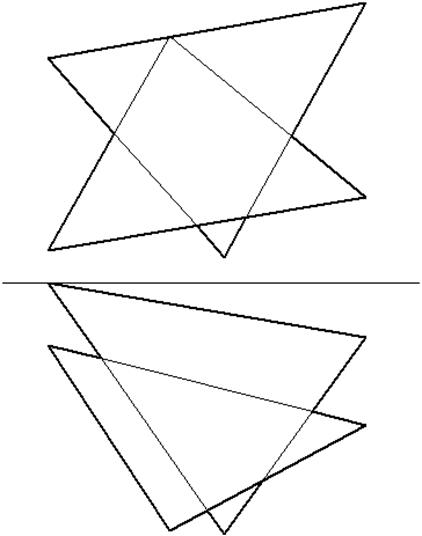
б) общим способом построения линии пересечения двух плоскостей

Вопросы для самоподготовки
1. Сформулируйте признак принадлежности:
а) точки и плоскости;
б) прямой и плоскости.
2. Какие линии плоскости относят к особым?
3. В чем заключается отличие восходящих плоскостей от нисходящих?
4. В каких случаях проекцией плоскости является прямая линия?
5. Какие метрические задачи можно решать без вспомогательных построений на эпюрах проецирующих плоскостей и плоскостей уровня?
6. Сформулируйте признаки параллельности и перпендикулярности:
а) прямой и плоскости;
б) двух плоскостей.
7. Как определяется на эпюре видимость:
а) прямой относительно плоскости;
б) одной плоскости относительно другой?
8. Как расположены линии уровня проецирующих плоскостей?
Задачи
1. Дать анализ расположения в пространстве плоскостей, изображенных на наглядном чертеже. Указать в таблице способ задания и вид плоскости.


 2. Указать в таблице видимость точек А и В относительно плоскости Г при проецировании на соответствующие плоскости проекций.
2. Указать в таблице видимость точек А и В относительно плоскости Г при проецировании на соответствующие плоскости проекций.


ТЕМА 5
Две ортогональные проекции геометрического образа определяют его положение в пространстве. Однако произвольное положение такого геометрического образа относительно плоскости проекций не всегда удобно для решения ряда позиционных и метрических задач. Здесь происходит искажение в проекциях проецируемых форм, отсутствует необходимая наглядность как объекта в целом, так и отдельных его элементов.
Во многих случаях решение задач значительно упрощается, если прямые линии и плоскости геометрического образа являются проецирующими относительно плоскостей проекций.
Различные требования к чертежу, а также необходимые условия для упрощения решения ряда позиционных и метрических задач требует построения новых, дополнительных проекций, исходя из двух заданных. Дополнительные проекции позволяют получить либо выраженные проекции отдельных элементов, либо их натуральные величины. Построение новых, дополнительных проекций называют преобразованием чертежа или проекций. Такое преобразование может быть выполнено следующими способами: плоскопараллельным перемещением, заменой плоскостей проекций, вращением, совмещением (частный случай вращения).
Плоскопараллельное перемещение можно рассматривать как вращение вокруг невыявленных проецирующих прямых. Здесь все точки геометрического образа перемещаются во взаимно параллельных плоскостях.
При плоскопараллельном перемещении геометрического образа одна из его проекций (оставаясь равной самой себе) перемещается в плоскости проекций, другие проекции точек геометрического образа перемещаются по прямым, параллельным направлению оси проекций.
Способ замены плоскостей проекций состоит в том, что одна из плоскостей проекций заменяется на новую плоскость, причем новая плоскость (заменяющая) остается в положении, перпендикулярном к незаменяемой плоскости проекций.
При замене фронтальной плоскости проекций координаты Z остаются неизменными. При замене горизонтальной плоскости проекций координаты Y не изменяются.
Для преобразования прямой общего положения в горизонталь необходимо заменить плоскость Н на Н1, а во фронталь – V на V1.
Для преобразования заданной плоскости общего положения в проецирующую необходимо новую плоскость проекций провести перпендикулярно заданной плоскости, т.е. перпендикулярно одной из главных линий заданной плоскости (горизонтали или фронтали). Если плоскость задана следами, то новую плоскость проекций проводят - перпендикулярно одному из ее следов.
Для определения натуральной величины плоской фигуры необходимо выполнить две замены плоскостей проекций.
Способ вращения заключается в том, что оригинал вращается вокруг оси, перпендикулярной к одной из плоскостей проекций. При этом все точки оригинала вращаются в плоскостях, перпендикулярных к оси вращения.
Если ось вращения перпендикулярна к горизонтальной плоскости проекций, то траектория движения точки на горизонтальной плоскости проекций проецируется в окружность. На фронтальной плоскости - эта траектория отобразится прямой, перпендикулярной к оси вращения.
При вращении отрезка прямой линии или плоской фигуры вокруг оси, перпендикулярной к плоскости проекций, проекция на эту плоскость не изменяется ни по виду, ни по величине. Меняется лишь положение этой проекции относительно оси проекций. Все точки прямой линии или плоской фигуры на другой плоскости проекций будут перемещаться по прямым перпендикулярным к оси вращения.
При плоскопараллельном перемещении каждая точка фигуры движется в плоскостях уровня. Перемещение осуществляется параллельно плоскостям проекций. Одна из проекций фигуры при этом не изменяет вида и величины, но изменяется ее положение относительно оси проекций. Другие проекции точек будут перемещаться по прямым параллельным оси проекций.
Задача № 17. Определить натуральную величину прямой АВ способом замены плоскостей проекций.

Задача № 18. Определить расстояние от точки С до прямой АВ способом замены плоскостей проекций.

Задача № 19. Преобразовать плоскость общего положения АВС в проецирующую способом замены плоскостей проекций.

Задача № 20. Преобразовать плоскость общего положения Р в проецирующую способом замены плоскостей проекций.
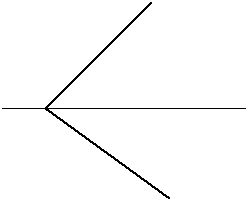
Задача № 21. Определить натуральные величины прямых АВ и АC методом вращения.

Задача № 22. Определить натуральную величину прямой АВ методом плоскопараллельного перемещения.

Задача № 23. Определить натуральную величину треугольника АВС методом плоскопараллельного перемещения и вращения.

Задача № 24. Преобразовать плоскость общего положения, заданную треугольником АВС, в горизонтально проецирующую методом плоскопараллельного перемещения.

Вопросы для самоподготовки
1. В чем сущность построения дополнительных проекций: а) точки; б) прямой; в) плоскости?
2. Как надо располагать дополнительные плоскости проекций, чтобы прямую общего положения преобразовать:
а) в прямую уровня;
б) в проецирующую прямую?
3. Как надо располагать дополнительные плоскости проекций, чтобы плоскость общего положения преобразовать:
а) в плоскость уровня;
б) в проецирующую плоскость?
4. Какие основные метрические задачи можно решать с помощью: проецирования на дополнительные плоскости проекций; вращения; плоскопараллельного перемещения?
5. Какие линии удобно выбирать в качестве осей вращения и почему?
Задачи
1. Какие проекции геометрических объектов не изменяют своего вида (и размеров) при плоскопараллельном движении? Объяснить на примере отрезка АВ, плоскости Т условно считаем прозрачными.

- Определить натуральные величины звеньев заданного механизма.

Тема 6,7
Кривые линии - это очертание многих инженерных конструкций и сооружений, деталей машин и механизмов, траектории движущихся точек.
Кривые линии на чертеже задаются проекциями рядаих точек.
Кривые линии, точки которых принадлежат плоскости, называются плоскими кривыми линиями. Если точки не принадлежат одной плоскости, то кривые линии называются пространственными.
Поверхность - это геометрическое место линий перемещающихся в пространстве. Производящая (образующая) кинематической поверхности перемещается в пространстве по определенному закону. От вида образующей и закона ее перемещения зависит форма (вид) кинематической поверхности.
Совокупность основных параметров поверхности, которые определяют ее задание, называют определителем поверхности.
Определителем конуса вращения может быть ось и образующая или вершина и направляющая линия.
Определителем цилиндра вращения может быть ось и образующая или ось и направляющая.
Поверхность тора может быть получена при вращении окружности L вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.
Поверхность сферы образуется в том случае, когда центр окружности принадлежит оси вращения.
На чертеже поверхность задается проекциями ее определителей. Для придания большей наглядности поверхности на чертеже вычерчивают ее очерк. Очерком поверхности называют линию пересечения с плоскостью проекций проецирующей поверхности, обертывающей данную поверхность.
Точки, лежащие на поверхности вращения должны лежать на их параллелях или образующих.
Поверхность многогранника ограничена плоскими многоугольниками. Элементами многогранника являются вершины, ребра и грани. Построение проекций многогранника сводится к построению проекций его элементов.
Чтобы построить проекции точки, лежащей на поверхности многогранника, необходимо "связать" эту точку с соответствующей гранью какой-либо прямой.
При пересечении поверхности плоскостью получается плоская фигура, называемая сечением.
При пересечении многогранника плоскостью в сечении получается многоугольник, число вершин многоугольника равно числу пересекаемых ребер многогранника.
При пересечении поверхности цилиндра плоскостями могут получаться следующие линии: окружность, эллипс, две образующие и одна образующая (при касании). При пересечении поверхности конуса плоскостями могут получаться: окружность, эллипс, парабола, гипербола, две пересекающиеся образующие.
Любая плоскость пересекает поверхность сферы по окружности.
Линию пересечения поверхности с плоскостью строят по точкам пересечения образующей поверхности в ряде ее положений с этой плоскостью.
Задача на нахождение точек пересечения прямой с какой либо поверхностью, в общем случае, может решаться по следующей схеме:
- через прямую проводится вспомогательная секущая плоскость;
- строится линия пересечения этой вспомогательной плоскости с поверхностью;
- точки пересечения, полученной линии сечения с заданной прямой, являются точками пересечения прямой с поверхностью;
- определяется видимость участков прямой линии.
В некоторых случаях следует применять в качестве вспомогательной плоскости плоскость общего положения, которая рассекает поверхность общего вида по простейшим линиям.
Для нахождения точек пересечения поверхности сферы с прямой применяют способ замены плоскостей проекций.
Поверхности двух геометрических тел могут пересекаться по одной и по двум замкнутым линиям. Одна линия пересечения получается при частичном пересечении поверхностей, когда одна из поверхностей "врезается" в другую. Две линии пересечения получаются при полном пересечении поверхностей.
Для того чтобы построить линию пересечения двух поверхностей, нужно найти ряд общих точек, принадлежащих им, и затем эти точки соединить в определенной последовательности.
Линией пересечения может быть:
- пространственная кривая – при пересечении двух кривых поверхностей;
- плоские кривые линии – при пересечении кривой поверхности и многогранника;
- пространственная ломаная линия – при пересечении двух многогранников.
Иногда линия пересечения двух поверхностей может оказаться плоской – прямой линией, окружностью, эллипсом и т.д.
Для того чтобы найти произвольную точку линии пересечения, поступают так:
1. вводят вспомогательную секущую плоскость (как правило, уровня чертеж;
2. находят линии пересечения этой плоскости с каждой поверхностью;
3. на пересечении найденных линий получают искомые точки.
Последовательно вводя ряд вспомогательных плоскостей, можно найти необходимое число точек.
Вспомогательную плоскость следует выбирать так, чтобы ее линия пересечения с каждой поверхностью проектировалась на плоскости проекций в виде простейших линий – прямой или окружности.
Линию пересечения двух многогранников можно найти и так:
1. находят точки пересечения ребер одного многогранника (А) с гранями другого (В);
2. находят точки пересечения ребер второго многогранника (В) с гранями первого (А);
3. найденные точки последовательно соединяют между собой прямыми линиями.
Соединяют между собой обязательно только те точки, которые принадлежат одним и тем же граням каждого многогранника.
Если хотя бы одна из поверхностей занимает проецирующее положение, то линию пересечения можно найти и таким образом: берутся точки на проецирующей поверхности через которые проводят образующие второй поверхности и находят общие точки этих поверхностей, а затем соединяют эти точки кривой линией согласно последовательности точек на проецирующей поверхности. Если фигура занимает фронтально-проецирующее положение, то таким способом определяются горизонтальные проекции точек линии пересечения. Если фигура занимает горизонтально-проецирующее положение, то таким способом определяются фронтальные проекции точек линии пересечения.
Иногда для того, чтобы найти точки линии пересечения кривых поверхностей, проще ввести не плоскость, а поверхность – шаровую (метод сфер).
Вспомогательные секущие концентрические сферы применяются для построения линии пересечения двух поверхностей вращения с общей плоскостью симметрии и пересекающимися осями. Каждая из этих поверхностей пересекается со сферами по окружностям, которые проецируются на одну из плоскостей проекций прямолинейными отрезками. В пересечении этих окружностей определяются общие точки двух заданных поверхностей.
При изучении кривых линий вы могли столкнуться с понятием касательной к плоскости и пространственной кривой. Прямая касательная к кривой поверхности представляет собой предельное положение прямой, пересекающей поверхность в двух точках, когда точки пересечения совпадают или можно сказать и так: касательной к поверхности называется такая прямая, которая касательна к какой-нибудь кривой, лежащей на поверхности.
Точка поверхности, в которой может быть проведена, и притом только одна, касательная плоскость, называется обыкновенной или правильной; обыкновенным точкам противопоставляются особые. Есть поверхности у которых не в каждой точке поверхности можно провести касательную, в некоторых точках касательная или неопределенная или не единственная такие точки называют особыми точками поверхностей.
Все касательные прямые в обыкновенной точке поверхности лежат в одной плоскости, следовательно, касательная плоскость является геометрическим местом всех касательных, проведенных к поверхности в одной точке. Очевидно, что для построения касательной плоскости в данной точке поверхности с помощью прямых, достаточно в этой точке провести к поверхности две касательные прямые.
С понятием касательной к плоскости неразрывно связано понятие нормали к поверхности. Прямую линию, проходящую через точку касания и перпендикулярную к касательной плоскости, называют нормалью поверхности в данной точке. Нормаль поверхности в данной точке определяет, следовательно, направление плоскости, касательной к поверхности в этой точке.
Понятие касательной плоскости играет весьма важную роль во всех областях геометрии. Подобно тому, как касательная к кривой плоской или пространственной позволяет изучить форму кривой вблизи точки касания, так и касательная плоскость может быть использована для исследования формы поверхности в окрестностях точки касания.
Вопросы для самоподготовки
1. Дайте классификацию кривых линий.
2. Какими основными свойствами (инвариантами) обладают ортогональные проекции линии?
3. Что значит «задать поверхность на чертеже»?
4. Сформулируйте признак принадлежности точки поверхности.
5. Какие элементы составляют эпюр поверхности?
6. Что такое: а) сечение поверхности; б) контур и очерк поверхности; в) каркас поверхности?
7. Что называют линиями среза поверхности вращения?
8. Какие поверхности можно получить в результате обработки материала:
а) сверлением; б) на токарном станке; в) на гончарном круге; г) на фрезерном станке; д) литьем; е) лазером.
Задачи
1. Определить длину заданной пространственной кривой.

2. Построить проекции траектории точки А, совершающей равномерное движение по прямой l, которая в свою очередь равномерно вращается вокруг оси. Известен шаг s (подъем за полный оборот точки) и радиус r вращения прямой l.




3. а) Построить проекции цилиндрической винтовой линии (гелисы) правого хода, заданной шагом s и радиусом r.
б) Построить проекции винтовой поверхности, заданной построенной гелисой и производящей. Производящая винтовой поверхности представлена равносторонним треугольником в главной меридиональной плоскости.

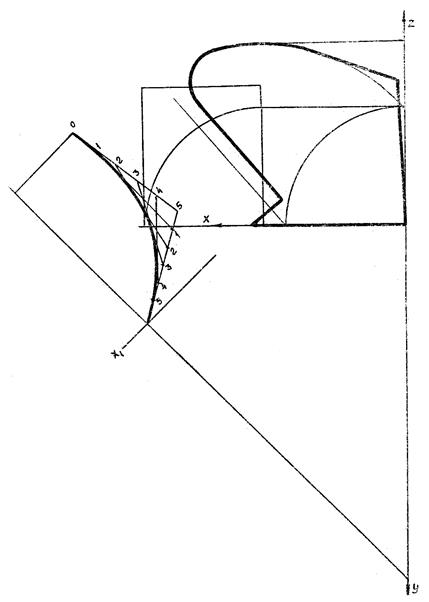
4. Заданы фронтальная проекция поверхности отвала плуга и направляющая – парабола, по которой перемещается горизонтальная образующая поверхности. Построить горизонтальную проекцию этой поверхности.
5. Построить недостающие проекции обозначенных точек поверхности, показав их видимость.
а)


б)

в)
 г)
г)
д)

6. Записать на полках линий-выносок номер положения плоскости, которой принадлежит указанное стрелкой соответствующее сечение тора.

Задача № 25. Построить недостающие проекции точек, лежащих на поверхностях.
а) б)



|
 | |||
 | |||
Задача № 26. Построить проекции линии пересечения многогранников плоскостями.
а)

б)

Задача № 27. Построить горизонтальную и профильную проекции шара, срезанного тремя плоскостями.

Задача № 28. Построить проекции точек пересечения прямой АВ с поверхностью.
а) б)

в)
д)

д)

Задача № 29. Построить натуральную величину сечения геометрического тела плоскостью.
а)

б)

Задача № 30. Построить три проекции геометрического тела, усеченного плоскостью частного положения, натуральную величину сечения, полную развертку и диметрическое изображение усеченной части тела

Задача № 31. Построить проекции линий пересечения поверхностей плоскостями частного положения. Определить натуральные величины сечений.
а)
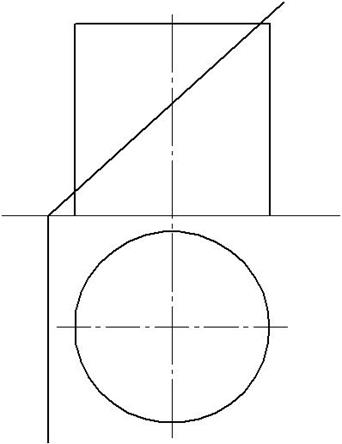
б)

Задача № 31. Построить проекции линии пересечения конуса плоскостью общего положения, натуральную величину сечения и полную развертку усеченной части

Задача № 32. Построить линии пересечения двух поверхностей
а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

л)

м)

Тема 8
Разверткой поверхности называется плоская фигура, полученная при совмещении всех точек поверхности с плоскостью.
Поверхность и ее развертка - это точечные множества между которыми устанавливается взаимно однозначное






