Лекции – 18 часов.
Практические занятия –18 часов.
Контрольная работа.
Всего часов 36.
| № п/п | Тема занятия | Кол. часов |
| Лекции | ||
| 1. | Двойные и тройные интегралы и их свойства. Представление об интегралах любой кратности. | |
| 2. | Вычисление двойных интегралов в декартовой системе координат. | |
| 3. | Замена переменных в кратных интегралах. Якобиан перехода. Переход к от декартовых полярным, цилиндрическим и сферическим координатам. | |
| 4. | Применение кратных интегралов для вычисления объёмов и площадей, для решения задач физики. | |
| 5. | Криволинейные интегралы первого рода, их свойства и способы нахождения. | |
| 6. | Криволинейные интегралы второго рода, их свойства и способы вычисления. | |
| 7. | Связь между криволинейными интегралами первого и второго рода. Формула Грина. | |
| 8. | Комплексные числа и действия над ними. Понятие функции комплексного переменного. | |
| 9. | Предел, непрерывность, производная функции комплексного переменного. Условия Коши-Римана. | |
| 10. | Дифференциальные уравнения первого порядка. Частное и общее решение. Задача Коши для уравнений первого порядка. Теорема существования и единственности. | |
| 11. | Интегрирование дифференциальных уравнений с разделяющимися переменными. Интегрирование линейных дифференциальных уравнений. Интегрирование дифференциальных уравнений Бернулли. | |
| 12. | Дифференциальные уравнения высших порядков. Задача Коши для дифференциального уравнения высшего порядка. Некоторые способы решения уравнения высшего порядка с помощью понижения порядка. Метод вариации произвольных постоянных (метод Лагранжа). Приемы решения линейных однородных дифференциальных уравнений с постоянными коэффициентами. | |
| 13. | Основные понятия комбинаторики (размещения, перестановки, сочетания). Основные понятия теории вероятностей. Относительная частота. Классическое определение вероятности. Теорема сложения вероятностей. Условные вероятности. Зависимые и независимые события. Теорема умножения вероятностей. | |
| 14. | Формула полной вероятности. Формула Байеса. Повторные независимые испытания. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Дискретные и непрерывные случайные величины. Функция распределения и ее свойства. Дискретные случайные величины. Ряд распределения. Числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение. | |
| 15. | Непрерывные случайные величины. Интегральная и дифференциальная функции распределения. Числовые характеристики непрерывных случайных величин. Числовые характеристики равномерного, показательного и нормального распределений. Закон больших чисел. | |
| 16. | Элементы математической статистики. Генеральная и выборочная совокупности. Эмпирическая функция распределения. Полигон и гистограмма. Статистические оценки параметров распределения. Точечные оценки неизвестных параметров. Понятие о доверительных интервалах и статистической проверке гипотез. | |
| Практические занятия | ||
| 1. | Вычисление двойных интегралов в декартовой системе координат. Замена переменных в кратных интегралах. Якобиан перехода. Переход к от декартовых полярным, цилиндрическим и сферическим координатам (по лекциям №1 и 2). | |
| 2. | Криволинейные интегралы первого рода, их свойства и способы нахождения. Криволинейные интегралы второго рода, их свойства и способы вычисления. Формула Грина (по лекции №3). | |
| 3. | Комплексные числа и действия над ними. Понятие функции комплексного переменного. Предел, непрерывность, производная функции комплексного переменного (по лекции №4). | |
| 4. | Дифференциальные уравнения первого порядка. Частное и общее решение. Задача Коши для уравнений первого порядка. Интегрирование дифференциальных уравнений с разделяющимися переменными. Интегрирование линейных дифференциальных уравнений. Интегрирование дифференциальных уравнений Бернулли (по лекциям №5 и 6). | |
| 5. | Задача Коши для дифференциального уравнения высшего порядка. Некоторые способы решения уравнения высшего порядка с помощью понижения порядка. Метод вариации произвольных постоянных (метод Лагранжа). Приемы решения линейных однородных с постоянными коэффициентами (по лекции №6). | |
| 6. | Определение вероятности. Решение задач с использованием основных теорем о вероятности случайных событий: сумма и произведение событий (по лекции №7). | |
| 7. | Формула полной вероятности. Формула Байеса. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Дискретные случайные величины. Числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение (по лекции №7). | |
| 8. | Непрерывные случайные величины и их числовые характеристики. Равномерное распределение. Показательное распределение. Нормальное распределение (по лекции №8). | |
| 9. | Элементы математической статистики. Эмпирическая функция распределения. Полигон и гистограмма. Статистические оценки параметров распределения. Точечные оценки неизвестных параметров. Понятие о доверительных интервалах и статистической проверке гипотез (по лекции №9). |
Рекомендуемая литература
1. В.С. Щипачев. Высшая математика (учебник). М.: Высшая школа 1998.
2. В.С. Щипачев. Задачник по высшей математике. М.: Высшая школа 2000.
3. Н.С. Пискунов. Дифференциальное и интегральное исчисление. Т.1 и 2. М.: Наука. 1970–1978.
4. В.Е. Гмурман Теория вероятностей и математическая статистика. М.: Высшая школа. 2001.
5. В.Е. Гмурман Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа. 2001.
6. В.И. Романов. Теория вероятностей (учебное пособие). М.: ГУЗ. 2003.
7. В.И. Романов. Методические указания. Статистика. М.:ГУЗ. 2005.
8. А.В. Червяков, А.Ю. Репин. Методические указания. Кратные и криволинейные интегралы, функции комплексного переменного, дифференциальные уравнения. М.: ГУЗ. 2005.
9. А.В. Червяков, А.Ю. Репин. Учебное пособие. Теория вероятностей и математическая статистика. М.: ГУЗ. 2006.
Вариант №1
Задача №1
Вычислить двойной интеграл 
от функции 
по заданной области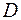 
:
, 
.
Задача №2
Вычислить объём тела 
с помощью кратного интеграла, используя подходящую замену переменных:
.
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой 
: 
, – отрезок с концами (1,1) и (2,3).
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками 
и 
и ориентированной в направлении от точки к точке :
, 
, 
.
Задача №5
Вычислить криволинейный интеграл по окружности 
, ориентированной по часовой стрелке:
.
Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы 
: 
.
Задача №7
Найти общее решение дифференциального уравнения:
.
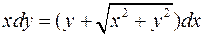Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию 
:
.
Задача №9
Решить задачу Коши:
, 
.
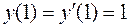Задача №10
Найти общее действительное решение однородного дифференциального уравнения: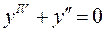 
.
Задача №11
Студент знает 20 из 25 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент знает: а) все три вопроса, содержащиеся в экзаменационном билете; б) только два вопроса своего экзаменационного билета; в) только один вопрос своего экзаменационного билета.
Задача №12
Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Используя асимптотические формулы, оценить, вероятность того, что в 225 испытаниях событие наступит не менее 170 и не более 185 раз.
Задача №13
Случайная величина 
может принимать только два значения 
и 
, причём 
. Известны вероятность 
возможного значения , математическое ожидание 
и дисперсия 
. Найти закон (ряд) распределения этой случайной величины. 
.
Задача №14
Случайная величина задана функцией распределения 
, требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
3) построить графики функции распределения и функции плотности распределения.
.
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение 
нормально распределённой величины . Найти: 1) вероятность того, что примет значение, принадлежащие интервалу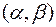 
; 2) вероятность того, что абсолютная величина отклонения 
окажется меньше 
.
.
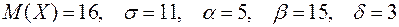Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг 
указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность 
.
4) При уровне значимости 
=0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 
, начало первого интервала 
, шаг 
.
Вариант №2
Задача №1
Вычислить двойной интеграл от функции по заданной области :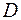
, 
.
Задача №2
Вычислить объём тела с помощью кратного интеграла, используя подходящую замену переменных:
.
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой : 
, – отрезок с концами (1,0) и (0,2).
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками и и ориентированной в направлении от точки к точке :
, 
, 
.
Задача №5
Вычислить криволинейный интеграл по окружности , ориентированной по часовой стрелке:
.
Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы : 
.
Задача №7
Найти общее решение дифференциального уравнения:
.
Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию : 
.
Задача №9
Решить задачу Коши:
, 
.
Задача №10
Найти общее действительное решение однородного дифференциального уравнения: 
.
Задача №11
Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,002, для второго – 0,003, для третьего – 0,004. Обрабатываемые детали складываются в один ящик. Производительность первого станка в три раза больше чем второго, а третьего в два раза меньше, чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.
Задача №12
Вероятность наступления события в каждом из одинаковых испытаний равна 0,001. Оценить вероятность того, что в 10000 испытаниях событие наступит 12 или 13 раз.
Задача №13
Случайная величина может принимать только два значения и , причём . Известны вероятность возможного значения , математическое ожидание и дисперсия . Найти закон (ряд) распределения этой случайной величины. 
.
Задача №14
Случайная величина задана функцией распределения , требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
3) построить графики функции распределения и функции плотности распределения.
.
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение нормально распределённой величины . Найти: 1) вероятность того, что примет значение, принадлежащие интервалу 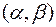; 2) вероятность того, что абсолютная величина отклонения окажется меньше .
.
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность .
4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 
, начало первого интервала 
, шаг .
Вариант №3
Задача №1
Вычислить двойной интеграл от функции по заданной области :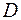
, 
.
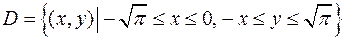Задача №2
Вычислить объём тела с помощью кратного интеграла, используя подходящую замену переменных:
.
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой :
, – граница треугольника с вершинами (0,0), (0,2), (2,0).
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками и и ориентированной в направлении от точки к точке :
, 
, 
.
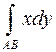Задача №5
Вычислить криволинейный интеграл по окружности , ориентированной по часовой стрелке:
.
Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы : 
.
Задача №7
Найти общее решение дифференциального уравнения:
.
Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию : 
.
Задача №9
Решить задачу Коши:
, 
.
Задача №10
Найти общее действительное решение однородного дифференциального уравнения: 
.
Задача №11
На овощехранилище поступает продукция от трёх хозяйств. Причём продукция первого хозяйства составляет 20%, второго – 46% и третьего – 34%. Известно, что средний процент нестандартных овощей для первого хозяйства равен 3%, для второго – 2%, для третьего – 1%. Найти вероятность того, что наудачу взятый овощ произведён на первом или втором хозяйстве, если он оказался нестандартным.
Задача №12
30% изделий данного предприятия – это продукция высшего сорта. Некто приобрел 6 изделий, изготовленных на этом предприятии. Чему равна вероятность того, что 4 или 5 из них высшего сорта?
Задача №13
Случайная величина может принимать только два значения и , причём . Известны вероятность возможного значения , математическое ожидание и дисперсия . Найти закон (ряд) распределения этой случайной величины: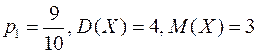 
.
Задача №14
Случайная величина задана функцией распределения , требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
3) построить графики функции распределения и функции плотности распределения.
.
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение нормально распределённой величины . Найти: 1) вероятность того, что примет значение, принадлежащие интервалу 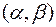; 2) вероятность того, что абсолютная величина отклонения окажется меньше .
.
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность .
4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 
, начало первого интервала 
,
шаг 
.
| –29 | –22 | –16 | –20 | –16 | –18 | –28 | –20 | –32 | –22 | –23 | –26 | –10 | –25 | –25 |
| –29 | –29 | –19 | –12 | –26 | –18 | –20 | –9 | –24 | –20 | –19 | –26 | –23 | –11 | –26 |
| –30 | –23 | –30 | –18 | –20 | –13 | –17 | –24 | –28 | –26 | –21 | –21 | –26 | –24 | –36 |
| –23 | –24 | –25 | –20 | –23 | –17 | –11 | –22 | –19 | –19 | –25 | –29 | –23 | –16 | –25 |
| –15 | –18 | –17 | –19 | –21 | –12 | –24 | –30 | –33 | –22 | –15 | –18 | –26 | –22 | –19 |
| –25 | –23 | –21 | –22 | –22 | –25 | –16 | –25 | –19 | –17 | –30 | –13 | –25 | –19 | –24 |
| –17 | –24 | –16 | –23 | –15 | –22 | –22 | –19 | –20 | –19 | –33 | –14 | –17 | –21 | –16 |
| –24 | –13 | –20 | –19 | –17 | –13 | –27 | –25 | –25 | –19 | –22 | –22 | –22 | –23 | –9 |
| –11 | –22 | –24 | –18 | –19 | –18 | –31 | –16 | –18 | –24 | –14 | –23 | –26 | –25 | –19 |
| –23 | –24 | –21 | –26 | –25 | –18 | –16 | –30 | –16 | –24 | –13 | –14 | –18 | –22 | –22 |
| –28 | –18 | –21 | –27 | –31 | –23 | –23 | –27 | –21 | –21 | –22 | –34 | –24 | –20 | –24 |
| –21 | –32 | –16 | –18 | –15 | –22 | –15 | –15 | –22 | –18 |
Вариант №4
Задача №1
Вычислить двойной интеграл от функции по заданной области :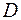
, 
.
Задача №2
Вычислить объём тела с помощью кратного интеграла, используя подходящую замену переменных:
.
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой : 
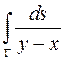, – отрезок с концами (0,–2) и (4,0).
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками и и ориентированной в направлении от точки к точке :
, , 
.
Задача №5
Вычислить криволинейный интеграл по окружности , ориентированной по часовой стрелке:
.
Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы : 
.
Задача №7
Найти общее решение дифференциального уравнения:
.
Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию : 
.
Задача №9
Решить задачу Коши:
, 
.
Задача №10
Найти общее действительное решение однородного дифференциального уравнения: 
.
Задача №11
На склад поступает продукция трёх фабрик. Причём продукция первой фабрики составляет 20%, второй – 45% и третьей – 35%. В продукции первой фабрики 5% нестандартных изделий, в продукции второй – 2%, третьей – 1%. Наудачу взятое изделие оказалось стандартным. Найти вероятность того, что оно произведено на первой или третьей фабриках.
Задача №12
Вероятность изготовления детали высшего сорта на данном станке равна 50%. Оценить вероятность того, что среди наудачу взятых 100 деталей половина окажется высшего сорта.
Задача №13
Случайная величина может принимать только два значения и , причём . Известны вероятность возможного значения , математическое ожидание и дисперсия . Найти закон (ряд) распределения этой случайной величины.
.
Задача №14
Случайная величина задана функцией распределения , требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
3) построить графики функции распределения и функции плотности распределения.
.
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение нормально распределённой величины . Найти: 1) вероятность того, что примет значение, принадлежащие интервалу 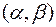; 2) вероятность того, что абсолютная величина отклонения окажется меньше .
.
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность .
4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 
, начало первого интервала 
, шаг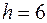 
.
Вариант №5
Задача №1
Вычислить двойной интеграл от функции по заданной области :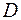
, 
.
Задача №2
Вычислить объём тела с помощью кратного интеграла, используя подходящую замену переменных:
.
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой :
, – граница треугольника с вершинами (0,0), (0,1), (1,0).
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками и и ориентированной в направлении от точки к точке :
, 
, .
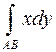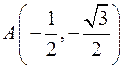Задача №5
Вычислить криволинейный интеграл по окружности , ориентированной по часовой стрелке:
.
Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы :
.
Задача №7
Найти общее решение дифференциального уравнения:
.
Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию : 
.
Задача №9
Решить задачу Коши:
, 
.
Задача №10
Найти общее действительное решение однородного дифференциального уравнения: 
.
Задача №11
Количество продукции, поступающей на обработку от трех цехов, определяется соотношением 3:4:5. На 100 единиц продукции первого цеха приходится в среднем 3 единицы брака, второго и третьего цехов, соответственно, 2 и 4 единицы. Наудачу взятая единица продукции оказалась годной. Какова вероятность того, что она поступила из второго цеха?
Задача №12
Вероятность наступления события в каждом из независимых испытаний равна 0,2. Оценить вероятность того, что событие в 100 испытаниях наступит не менее 20 раз и не более 30 раз.
Задача №13
Случайная величина может принимать только два значения и , причём . Известны вероятность возможного значения , математическое ожидание и дисперсия . Найти закон (ряд) распределения этой случайной величины: 
.
Задача №14
Случайная величина задана функцией распределения , требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
3) построить графики функции распределения и функции плотности распределения.
.
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение нормально распределённой величины . Найти: 1) вероятность того, что примет значение, принадлежащие интервалу 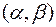; 2) вероятность того, что абсолютная величина отклонения окажется меньше .
.
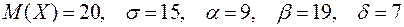Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность .
4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 
, начало первого интервала 
, шаг
