ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Контрольная работа 2
по дисциплине «Высшая математика 1»
Выполнил:
Пан философ
Вариант2.8
Задание № 1.
Даны координаты вершин треугольника А(1,3), В(2,8), С(6,7). Записать общее уравнение его высоты АН.
Решение.
Уравнение прямой, проходящей через две точки, имеет вид:

тогда уравнение ВС примет вид:
 -1*(x-2)=4(y-8); 4y+x-34=0;
-1*(x-2)=4(y-8); 4y+x-34=0;

 -уравнение ВС и
-уравнение ВС и  .
.
По условию высота АН ^ ВС, тогда  .
.
Уравнение АН принимает вид: y=4x+b.
Так как АÎАН, то 3=4+b,b=-1 и y=4x-1 – уравнение высоты.
Ответ: 4x-y-1=0.
Задание № 2
В треугольнике АВС из вершины А проведены высота и медиана. Даны:
Вершина В(6,5), уравнение высоты x+y=2 и уравнение медианы 2x-3y+1=0.
Найти координаты вершины С.
Решение.
1. Координаты т.А находим из условия:

 ÞА(1;1).
ÞА(1;1).
2. А) Высота АН ^ ВС. Уравнение высоты АН: x+y=2 т.е. y=-x+2 и 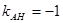 . Тогда
. Тогда 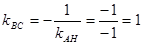

Уравнение ВС принимает вид: y=x+b. Поскольку т.В(6,5) лежит на этой прямой, то 5=6+b, b=-1 и прямая ВС задана уравнением y=x-1.
Б) Координаты т.М находим из условия: М=АМ  ВС,
ВС, 
Т.е.  ; M=(4;3).
; M=(4;3).
B(6;5) M(4;3) C(?)
 |
Отсюда,  =2*4-6=2;
=2*4-6=2;  =2*3-5=1, C(2;1).
=2*3-5=1, C(2;1).
Ответ: С(2;1).
Задание № 3
Записать общее уравнение плоскости, проходящей через точки
 (1,-2,4) и
(1,-2,4) и  (2,-1,2) перпендикулярно плоскости x+4y-5z+3=0.
(2,-1,2) перпендикулярно плоскости x+4y-5z+3=0.
Решение:
За нормальный вектор 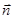 плоскости ά принимаем векторное произведение векторов
плоскости ά принимаем векторное произведение векторов 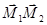 =(1;1;-2) и
=(1;1;-2) и 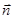 = (1;4;-5).Таким образом,
= (1;4;-5).Таким образом,

=3i+3j+3k.
Воспользуемся уравнением плоскости, проходящей через данную точку
 (1,-2,4) перпендикулярно вектору
(1,-2,4) перпендикулярно вектору 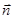 =(3;3;3):
=(3;3;3):
3(x-1)+3(y+2)+3(z-4)=0;
3x-3+3y+6+3z-12=0
3x-3y+3z-9=0
x-y+z-3=0.
Ответ: x-y+z-3=0.
Задание № 4.
Найти координаты проекции точки М(3,-1,-3) на плоскость 2x+y-4z+4=0
Решение:
Пусть  - проекция т.М на плоскости. Находим т.
- проекция т.М на плоскости. Находим т.  как точку пересечения прямой ℓ, проходящей через т.М перпендикулярно данной плоскости.
как точку пересечения прямой ℓ, проходящей через т.М перпендикулярно данной плоскости.
Прямая ℓ параллельна вектору нормами 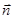 =(2;1;-4) плоскости, поэтому вектор
=(2;1;-4) плоскости, поэтому вектор 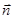 является направляющим для этой прямой.
является направляющим для этой прямой.
Параметрические уравнения этой прямой ℓ:

Находим точку пересечения прямой с плоскостью:
2(2t+3)+(t-1)-4(-4t-3)+4=0
4t+6+t-1+16t+12+4=0
21t=-21, t=-1
Значит  (1;-2;1)
(1;-2;1)
Ответ: (1;-2;1)
Задание № 5.
Найти коэффициент А в уравнении плоскости Ax+y+Cz+D=0, проходящей через точки Р(1,1,8), О(0,0,0) параллельно прямой  .
.
Решение:
Данная плоскость параллельна векторам  и
и 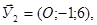 поэтому её вектор нормали
поэтому её вектор нормали 
Тогда уравнение плоскости 14х+(-6)y-z+D=0
Итак А=14
Ответ: 14
Задание № 6.
При каких значениях параметров а и с прямая  пересекает две другие прямые
пересекает две другие прямые 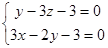 и
и 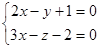
Решение:
Пусть уравнение 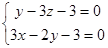 задаёт прямую
задаёт прямую  ,
,
Уравнение 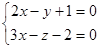 задаёт прямую
задаёт прямую  .
.
Перейдём к каноническим уравнениям:  :
: 
Полагая z=t, получим: 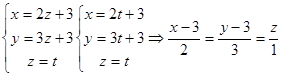
 :
: 
Полагая z=t, получим: 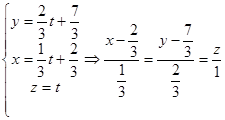
Условия пересечения двух прямых является условие: ( )=0
)=0
Имеем: 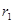 =(1;1;-1),
=(1;1;-1),  =(3;3;0),
=(3;3;0),  =(а;-1;с),
=(а;-1;с),  =(2;3;1)
=(2;3;1)
Находим: 
Аналогично: 
Находим:  ;
;
-а+с+1=0
Тогда: 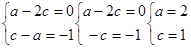
Ответ: а=2; с=1.
Задание № 7.
Найти радиус сферы, если известно, что она касается двух плоскостей
x-2y+2z+22=0 и x-2y+2z+10=0.
Решение:
Плоскости ά и β, задаваемые соответственно уравнениями x-2y+2z+22=0(ά) и
x-2y+2z+10=0(β), параллельны, т.к. 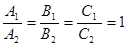 .
.
Тогда плоскости ά и β перпендикулярны диагональному сечению сферы, содержащему обе точки касания сферы и плоскостей.
Значит r =  =d(A;B), где АÎ ά.
=d(A;B), где АÎ ά.
Пусть y=z=0, тогда А(-22;0;0) и АÎ ά.
Находим расстояние от этой точки до плоскости β.
Воспользуемся формулой: d= 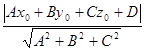
Имеем: d= 
Тогда расстояние плоскостями равно r=  .
.
Ответ: r=  .
.
Задание № 8.
Дана кривая 
Решение:
Преобразуем уравнение:




Пусть x-2=X, y-8=Y, тогда уравнение примет вид:  уравнение эллипса, где
уравнение эллипса, где 
2. Находим центр симметрии:
x-2=0 y-8=0
x=2 y=8
Тогда (2;8)-центр симметрии эллипса.
3. Так как  то а=2 – большая полуось эллипса, в=3 – малая полуось эллипса.
то а=2 – большая полуось эллипса, в=3 – малая полуось эллипса.
4. Уравнение фокальной оси: х=2.
5. Построим эллипс:

 y y´
y y´
 |
8 2 x´
 |
x

 0 1 2
0 1 2
Ответ: 2) О´(2;8)- центр симметрии
3) а=2, в=3
4) х=2 –уравнение фокальной оси.
Задание № 9
Дана кривая 
Решение:
1. Преобразуем уравнение:


Пусть х-2=Х, y-5=Y, тогда уравнение примет вид:  - уравнение параболы.
- уравнение параболы.
2. Вершину параболы находим из условия: х-2=0, х=2. y-5=0, y=5
А(2;5)-вершина параболы.
3. Итак,  ,тогда 2р=(-8), р=4.
,тогда 2р=(-8), р=4.
4. Осью симметрии параболы, имеющее вид  является ось 0Y, тогда осью симметрии исходной параболы является прямая х=2.
является ось 0Y, тогда осью симметрии исходной параболы является прямая х=2.
5. Построим параболу:
y y´
 |  |
5 -1 0´ 1 x´

 -1
-1
 x
x
0 1 2
Ответ:
2) A(2;5)-координаты вершины параболы.
3) р=4.
4) х=2 – уравнение оси симметрии.
Задание № 10
Дана кривая 
Решение:
Квадратичную форму В(x;y) =  приводим к главным осям. Для этого записываем матрицу этой квадратичной формы В=
приводим к главным осям. Для этого записываем матрицу этой квадратичной формы В= 
И находим её собственные числа и собственные векторы. Запишем и решим характеристическое уравнение матрицы В:

 -собственные числа. Так как эти числа разных знаков, то данное уравнение определяет кривую гиперболического типа. Находим собственные векторы матрицы В. Для числа
-собственные числа. Так как эти числа разных знаков, то данное уравнение определяет кривую гиперболического типа. Находим собственные векторы матрицы В. Для числа  , получаем систему:
, получаем систему:
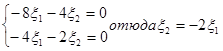
Полагая 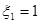 , находим единичный собственный вектор
, находим единичный собственный вектор 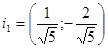
Для числа  , получаем систему:
, получаем систему:  ;
; 
Полагая 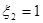 , находим
, находим 
Базис  принят правым.
принят правым.
От старого базиса  перейдём к новому
перейдём к новому  .
.
Матрица перехода имеет вид: 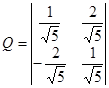 ,
, 
Старые координаты связаны с новыми  соотношениями:
соотношениями:  , или:
, или: 

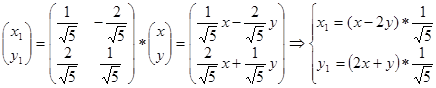
В новой системе координат уравнение данной кривой имеет вид:

Отсюда действительная полуось а=1, а мнимая b=3. Произведём преобразование параллельного переноса системы координат в новое начало  по формулам:
по формулам:

В системе координат ( ) гипербола имеет уравнение:
) гипербола имеет уравнение: 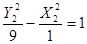
Оси  и
и  направлены по прямым x-2y+1=0, 2x+y-3=0.
направлены по прямым x-2y+1=0, 2x+y-3=0.
Координаты точки  являющиеся центром симметрии гиперболы, находим, решая систему:
являющиеся центром симметрии гиперболы, находим, решая систему: 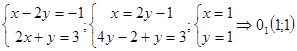
Фокальной осью является прямая  , т.е. 2x+y-3=0.
, т.е. 2x+y-3=0.
Прямые  асимптоты.
асимптоты.



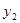 y
y
 | |||
 | |||







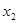
 3
3
 |
1  1
1
x
0 1
 |
-3
Ответ:
2)  (1;1) –координаты центра симметрии
(1;1) –координаты центра симметрии
3) а=1 – действительная полуось
в=3 – мнимая полуось
4) 2x+y-3=0 – уравнение фокальной оси.






