Воронеж
Утверждено научно-методическим советом
Математического факультета 28.05.03.
Составитель: Каплан А.В.
Практикум подготовлен на кафедре теории функций и геометрии
математического факультета Воронежского государственного университета.
Рекомендуется для студентов 1 курса биолого-почвенного факультета
(отделение агрохимии и почвоведения).
От составителя.
Настоящий практикум содержит условия контрольных работ по курсу «Высшая математика» для студентов 1 курса отделения агрохимии и почвоведения биолого-почвенного факультета.
В течение учебного года студенты выполняют 6 контрольных работ: работы №№ 1 – 3 выполняются в первом семестре, работы №№ 4 – 6 – во втором.
Номера «своих» вариантов студенты узнают на практических занятиях. Для более полного и глубокого усвоения учебного материала рекомендуется выполнить несколько заданий из «чужих» вариантов.
Каждое задание должно быть выполнено на отдельном одинарном листе, все задания вкладываются в двойной лист, на первой странице которого студент указывает фамилию и имя, номер группы и номер своего варианта. Кроме того, на этой странице заготавливается решетка для оценок (первая строка – номера заданий, вторая – пустые клетки для оценок).
Образец:
Выполнение всех работ на оценку не ниже 3,0 необходимо и достаточно для получения зачета в первом семестре и допуска к экзамену – во втором.
Желаю успеха!
А.В.Каплан.
Контрольная работа №1
Аналитическая геометрия».
Задание 1. Прямая линия.
Дано уравнение прямой ℓ и точка М (х 0; у 0).
1) Найти расстояние от точки М до прямой ℓ.
2) Привести уравнение прямой ℓ к виду в отрезках.
3) Найти площадь S треугольника, отсекаемого прямой ℓ на осях
координат.
4) Написать уравнение прямой ℓ ^, проходящей через точку М и
перпендикулярной ℓ.
5) Найти точку P пересечения полученной прямой ℓ ^ и прямой ℓ.
| Номер | Уравнение прямой ℓ | Точка М (х 0; у 0) |
| 1. | 2 х + у + 1 = 0 | М (2; 1) |
| 2. | х – 2 у + 1 = 0 | М (–1; 2) |
| 3. | 2 х – у + 1 = 0 | М (2; –1) |
| 4. | х + у + 1 = 0 | М (1; 1) |
| 5. | х – у + 1 = 0 | М (1; –1) |
| 6. | х +2 у + 1 = 0 | М (1; 2) |
| 7. | х – у – 1 = 0 | М (–1; –1) |
| 8. | х + у – 1 = 0 | М (–1; 1) |
| 9. | х + 2 у – 1 = 0 | М (1; –2) |
| 10. | 2 х – у – 1 = 0 | М (2; 2) |
Задание 2. Окружность.
Дано уравнение окружности.
1) Привести это уравнение к каноническому виду.
2) Найти координаты центра.
3) Найти радиус.
4) Найти точки пересечения окружности с осью абсцисс.
5) Найти точки пересечения окружности с осью ординат.
| Номер | Уравнение окружности | Номер | Уравнение окружности |
| 1. | х 2 + у 2 – 2 х + 2 у – 1 = 0 | 6. | х 2 + у 2 – 10 х – 6 у + 33 = 0 |
| 2. | х 2 + у 2 – 4 х – 2 у + 1 = 0 | 7. | х 2 + у 2 – 8 х + 6 у = 0 |
| 3. | х 2 + у 2 – 4 х + 2 у + 1 = 0 | 8. | х 2 + у 2 – 2 х – 4 у + 1 = 0 |
| 4. | х 2 + у 2 – 2 х + 2 у + 1 = 0 | 9. | х 2 + у 2 – 4 х + 4 у + 4 = 0 |
| 5. | х 2 + у 2 + 2 х + 4 у + 1 = 0 | 10. | х 2 + у 2 + 2 х + 2 у + 1 = 0 |
Задание 3. Эллипс.
Известно, что точка М (х 0; у 0) принадлежит эллипсу, заданному в канонической системе координат. Кроме того, задано еще некоторое дополнительное условие.
1) Составить каноническое уравнение эллипса.
2) Определить параметры a, b, c эллипса.
3) Найти координаты фокусов и вычислить эксцентриситет.
4) Написать уравнения директрис.
5) Найти фокальные радиусы данной точки М.
| Номер | Точка М (х 0; у 0) | Дополнительное условие |
| 1. | М (2;  ) )
| 
|
| 2. | М (–  ; 2) ; 2)
| 
|
| 3. | М (8; 12) | | MF 1 | = 20 |
| 4. | М ( ;–1) ;–1)
| | F 1 F 2 | = 8 |
| 5. | М (4; –  ) )
| точка N (2  ; 3) Î эллипсу ; 3) Î эллипсу
|
| 6. | М (2; –2) | а = 4 |
| 7. | М (–2  ; 2) ; 2)
| b = 3 |
| 8. | М ( ; ;  ) )
| F 1 (–1; 0) |
| 9. | М (4; 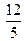 ) )
| F 2 (3; 0) |
| 10. | М (2;  ) )
| 
|
Задание 4. Гипербола.
Дано каноническое уравнение гиперболы.
1) Найти полуоси.
2) Определить координаты фокусов.
3) Вычислить эксцентриситет.
4) Написать уравнения асимптот.
5) Написать уравнения директрис.
| Номер | Уравнение гиперболы | Номер | Уравнение гиперболы |
| 1. | 
| 6. | 
|
| 2. | 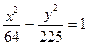
| 7. | 
|
| 3. | 
| 8. | 
|
| 4. | 
| 9. | 
|
| 5. | 
| 10. | 
|
Задание 5. Парабола.
В некоторой системе координат задано уравнение параболы.
1) Определить координаты вершины и указать направление оси.
2) Найти величину параметра.
3) Определить координаты фокуса.
4) Написать уравнение директрисы.
5) Найти точки пересечения параболы с осями координат.
| Номер | Уравнение параболы | Номер | Уравнение параболы |
| 1. | у 2 – 4 х – 6 у + 29 = 0 | 6. | у 2 – 6 х + 14 у + 49 = 0 |
| 2. | х 2 + 2 х + у = 0 | 7. | у 2 + 8 х – 16 = 0 |
| 3. | у 2 – х – 6 у – 8 = 0 | 8. | х 2 – 6 х – у + 8 = 0 |
| 4. | у 2 – 10 х – 2 у – 19 = 0 | 9. | у 2 + х – 2 у – 3 = 0 |
| 5. | х 2 – 2 х + у – 3 = 0 | 10. | у 2 + х + 2 у = 0 |
Контрольная работа №2
Пределы».
Задание 1.
Вычислить пределы и доказать правильность вычислений на «языке e – N».
1.. 6..
2.. 7..
3.. 8..
4.. 9..
5.. 10..
Задание 2.
Вычислить пределы:
1.. 6..
2.. 7..
3.. 8..
4.. 9..
5.. 10..
Задание 3.
Вычислить пределы:
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
Задание 4.
Вычислить пределы:
1.. 6..
2.. 7..
3.. 8..
4.. 9..
5.. 10..
Задание 5.
Вычислить пределы:
1.. 6..
2.. 7..
3.. 8..
4.. 9..
5.. 10..
Контрольная работа №3
Производные».
В заданиях 1. – 5. вычислить производные указанных функций.
Задание 1. Задание 2.
1.  . 1.
. 1.  .
.
2.  . 2.
. 2.  .
.
3.  . 3.
. 3.  .
.
4.  . 4.
. 4.  .
.
5.  . 5.
. 5.  .
.
Задание 3.\ Задание 4.
1.  . 1.
. 1.  .
.
2.  . 2.
. 2.  .
.
3.  . 3.
. 3.  .
.
4.  . 4.
. 4.  .
.
5.  . 5.
. 5.  .
.
Задание 5.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  .
.
Контрольная работа №4
Исследование функций».
Задание 1.
Считая известными графики элементарных функций, построить графики указанных сложных функций.
1. y = e arc tg x . 2. y = ln (cos x).
3. y = e cos x . 4. y = ln (sin x).
5. y = e  . 6. y =
. 6. y =  .
.
7.  . 8.
. 8.  .
.
9. y = 2  . 10.
. 10.  .
.
Задание 2.
Найти асимптоты графиков следующих функций.
1. y =  . 2. y =
. 2. y =  .
.
3. y =  . 4.
. 4.  .
.
5. y =  . 6. y =
. 6. y =  .
.
7.  . 8.
. 8. 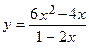 .
.
9. y =  10. y =
10. y =  .
.
Задание 3.
Найти промежутки монотонности и экстремумы следующих функций (рассмотреть промежуток [ – p; p ]).
1. y = sin x + cos x. 2. y =  sin x + cos x.
sin x + cos x.
3. y = sin x – cos x. 4. y = cos 2 x – 2sin x.
5. y = sin x + cos 2 x. 6. y = cos x – sin x.
7. y = sin x +  cos x. 8. y = sin x –
cos x. 8. y = sin x –  cos 2 x.
cos 2 x.
9. y = cos x +  cos 2 x. 10. y =
cos 2 x. 10. y =  sin x – cos x.
sin x – cos x.
Задание 4.
Найти промежутки выпуклости и точки перегиба графиков следующих функций.
1.  . 2. y = e
. 2. y = e  .
.
3. y = х 2 ln x. 4. y = x е – х .
5.  . 6. y = (1 + х 2) е х .
. 6. y = (1 + х 2) е х .
7. y = х ln 2 x. 8. y = х 3 е – х .
9. y =  . 10. y = е х (х 2 – 2 x + 2).
. 10. y = е х (х 2 – 2 x + 2).
Задание 5.
Исследовать функции и построить графики.
1. у = 2 х 3 – 9 х 2 + 12 x – 5. 2. у = 2 х 3 + 15 х 2 + 36 x – 53.
3. у = х 3 – 12 x + 11. 4. у = х 3 – 3 х 2 – 9 x – 11.
5. у = 2 х 3 – 9 х 2 + 7. 6. у = 2 х 3 + 9 х 2 + 12 x – 23.
7. у = 2 х 3 – 15 х 2 + 36 x – 23. 8. у = х 3 – 3 x + 2.
9. у = х 3 + 3 х 2 – 9 x + 5. 10. у = 2 х 3 + 9 х 2 – 11.
Контрольная работа №5
Неопределенный интеграл».
В заданиях 1. – 5. вычислить интегралы.
Задание 1.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 2.
1. 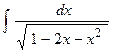 . 2.
. 2. 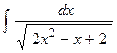 .
.
3. 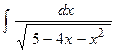 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 3.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 4.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 5.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Контрольная работа №6
Определенный интеграл и его приложения».
Задание 1.
Вычислить интегралы с помощью указанных подстановок.
1. 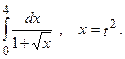 2.
2.  3.
3.  4.
4. 
5.  6.
6. 
7. 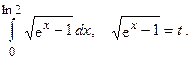 8.
8. 
9.  10.
10. 
Задание 2.
Вычислить интегралы.
1.  2.
2. 
3.  4.
4.  .
.
5.  . 6.
. 6.  .
.
7.  8.
8. 
9.  . 10.
. 10.  .
.
Задание 3.
Вычислить несобственные интегралы.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 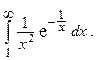
7.  8.
8. 
9. 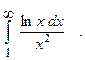 10.
10. 
Задание 4.
Вычислить площадь фигуры, ограниченной заданными
линиями.
1.  ; y = x; x = 0.
; y = x; x = 0.
2.  ; y = 2 – x; y = 0.
; y = 2 – x; y = 0.
3.  ; y = x + 2.
; y = x + 2.
4.  ; y = 3 x – 1.
; y = 3 x – 1.
5.  ; y = x.
; y = x.
6.  ; y = 2(1 – x); x = 0
; y = 2(1 – x); x = 0
7.  ; y = 4(x – 2); y = 0.
; y = 4(x – 2); y = 0.
8.  ; y = 3 x.
; y = 3 x.
9.  ; y = 10 – x.
; y = 10 – x.
10.  ; x + y =
; x + y =  .
.
Задание 5.






