Ознакомление с понятиями линейной зависимости системы векторов, базой, базисом, суммой и пересечением подпространств, приобретение практических навыков решения и исследования на совместность СЛАУ.
3. Ознакомление с понятиями ортогонального дополнения, проекции вектора на подпространство, орта вектора к подпространству, ортогональной системы векторов и процедурой ортогонализации Грама – Шмидта.
Образец РГЗ №1 (по частям):
1. a) Вычислите определитель матрицы размера 4х4, воспользовавшись его определением и свойствами.
б) Вычислите определитель матрицы из п. а), разложив его по элементам какой-либо строки и какого-либо столбца.
в) Вычислите определитель матрицы из п. а), разложив его по двум и трем каким-либо строкам (столбцам).
г) Решите крамеровскую СЛАУ методом обратных матриц и проверьте по формуле Крамера одну из компонент решения.
2. а) Найдите все базы каждой из двух систем векторов. Определите, эквивалентны ли эти системы. Для каждой из систем векторов найдите такую базу, чтобы линейно – зависимые векторы системы выражались через векторы базы в виде линейной комбинации с целыми коэффициентами. Запишите соответствующие выражения.
б) Найдите базисы суммы и пересечения подпространств 
и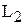 
, натянутых на заданные системы векторов.
в) Исследуйте совместность и запишите общее решение неоднородной СЛАУ в виде суммы частного решения этой системы и линейной комбинации базисных решений соответствующей однородной системы.
3. а) Спроектируйте заданный вектор x на заданное подпространство L. Найдите длину наклонной, перпендикуляра и проекции, а также угол между наклонной и подпространством.
б) Выполните ортогонализацию базиса двумерного подпространства L и дополните его до ортогонального базиса пространства 
.
Цели РГЗ №2 (по частям):
1. Приобретение практических навыков приведения уравнения поверхности второго порядка к каноническому виду.
2. Приобретение практических навыков построения жордановой нормальной формы линейного оператора, заданного своей матрицей.
Образец РГЗ №2 (по частям):
1. Поверхность задана уравнением в исходной декартовой прямоугольной системе координат. Приведите уравнение к каноническому виду и определите тип поверхности. Найдите каноническую систему координат. Сделайте проверку. Выполните рисунок поверхности в канонической системе координат. Проверьте правильность нахождения канонического уравнения по инвариантам.
2. Линейный оператор задан матрицей размера 4x4 в некотором базисе. Постройте жорданову нормальную форму матрицы и укажите соответствующий канонический базис. Сделайте проверку.
