Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом.
Домашнее задание: № 13 (учебник); № 109 (рабочая тетрадь).
Урок 38
Окружность, ее центр и радиус.
Окружность и круг
Цели урока: продолжить формирование умений строить окружности с помощью циркуля; совершенствовать навыки решения задач с величинами «цена», «количество», «стоимость»; вести подготовительную работу по выделению среди четырехугольников группы прямоугольников; развивать логическое мышление и умение обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.
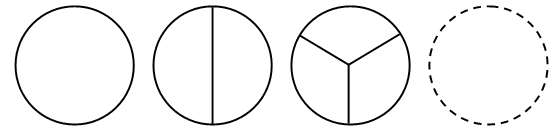
2. Решите задачу.
Витя и Дима играют в бадминтон. Первая партия закончилась со счетом 11: 5 в пользу Вити. Вторая партия – со счетом 11: 7 в пользу Димы.
а) Кто набрал очков больше?
б) На сколько у одного мальчика очков больше, чем у другого?
– Подумайте, на какой из этих вопросов можно ответить, не выполняя арифметического действия.
3. Вставьте знаки арифметических действий, чтобы получились верные равенства.
| 12 … 5 …2 = 9 | 6 … 8 … 6 = 8 |
| 16 … 9 … 2 = 9 | 12 … 9 … 5 = 8 |
| 11 … 7 … 5 = 9 | 12 … 3 … 1 = 8 |
| 13 … 7 … 3 = 9 | 17 … 4 … 5 = 8 |
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
– Чем похожи и чем отличаются рисунки слева и справа?

Учащиеся. Слева и справа нарисованы замкнутые кривые линии. На каждой из них отмечены 4 точки. Точка О находится внутри замкнутой линии на левом и на правом рисунках.
– Вы назвали признаки, по которым рисунки похожи. А чем они отличаются?
Учащиеся. На левом рисунке все точки, которые отмечены на замкнутой кривой, находятся на одинаковом расстоянии от точки О, а на правом рисунке это условие не выполняется.
– Поставьте на одной и на другой линии слева еще 4 любые точки. На каком расстоянии от точки О они будут находиться?
Замкнутая кривая слева – окружность.
Точка О – центр окружности.
– С помощью какого инструмента можно провести окружность?
– Сегодня на уроке будем закреплять умение строить окружности.
IV. Работа по теме урока.
1. Работа по учебнику.
Задание № 12 (с. 74).
– Рассмотрите чертеж. Что здесь изображено? (Многоугольник, четырехугольник, прямоугольник, квадрат.)
– Назовите более точное название этой фигуры. (Квадрат.)
– Укажите свойства квадрата.
– Сравните с помощью циркуля длины сторон квадрата. Какой вывод можно сделать?
| Квадрат – это прямоугольник, у которого все стороны равны |
– Сколько измерений надо выполнить, чтобы найти периметр квадрата? (Одно измерение.)
– Как вычислить периметр многоугольника?
– Найдите периметр квадрата.

Задание № 14 (с. 74).
– Рассмотрите рисунок. Что вы узнали?
– Прочитайте текст задания. Что требуется узнать?
– Запишите условие задачи в таблицу.
| Наименование товара | Цена | Количество | Стоимость |
| Печенье | 12 р. | 3 п. | ? р. |
| Шоколад | 18 р. | 2 пл | ? р. |
| Конфеты | 56 р. | 1 к. | |
| Вафли | 10 р. | 2 п. | ? р. |
Было – 50 рублей.
Решение:
1. Сколько стоят 2 плитки шоколада?
18 + 18 = 36 (р.).
2. Сколько стоят пачка печенья и шоколадка?
12 + 18 = 30 (р.).
3. Сколько стоят пачка вафель, пачка печенья и плитка шоколада?
10 + 12 + 18 = 40 (р.).
4. Сколько стоят 3 пачки печенья?
12 + 12 + 12 = 36 (р.).
5. Сколько стоят 2 пачки вафель, шоколадка и пачка печенья?
10 + 10 + 18 + 12 = 50 (р.).
Задание № 16 (с. 75).
– Прочитайте задание. Выполните рисунок к условию.
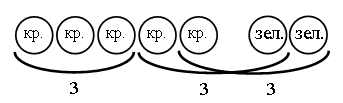
– Остался ли в коробке хотя бы один красный шар? (Да.)
– Мог ли остаться в коробке хотя бы один зеленый шар? (Мог остаться, если бы взяли все красные шары или два красных и один зеленый.)
V. Самостоятельная работа по теме «Окружность, ее центр и радиус».
Задание № 1.
– Выберите рисунок, на котором все точки линии находятся на одинаковом расстоянии от точки О.
– Как называется такая линия?

Задание № 2.
– Рассмотрите рисунки.

– Как получили такие красивые узоры?
– Попробуйте начертить такие же узоры.
– Придумайте свои узоры из окружностей.
Задание № 3.
– Измерьте длину радиусов каждой окружности:

– Что о них можно сказать? (Радиусы одной окружности равны между собой.)
– Начертите несколько своих окружностей и проведите в каждой несколько радиусов. Радиусы каждой из них равны?
– Вы согласны, что все точки окружности находятся на одинаковом расстоянии от ее центра? Объясните свой ответ.
Задание № 4.
Можно ли провести окружность с центром в точке О так, чтобы она проходила через точки А, В, С, D?

Задание № 5.
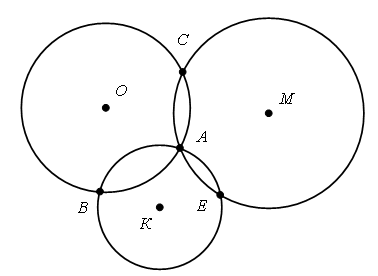
Какие точки лежат на окружностях:
а) с центром в точке О и с центром в точке М?
б) с центром в точке М и с центром в точке К?
VI. Итог урока.
– Рассмотрите рисунок 1 на доске.

– Что на нем изображено?
– Как называется отрезок ОА?
– Подумайте, есть ли на рисунке другие радиусы этой окружности?
– Назовите их. (ОВ, OD, OC, OK.)
– Что же такое радиус? (Радиус – это отрезок, который соединяет центр окружности с точкой окружности.)
– Рассмотрите второй рисунок на доске.

– Назовите имена линий, которые не являются радиусами. (СВ, OY, OX, OК, РК.)
– Начертите окружность с радиусом 4 см. Проведите в ней красным цветом 3 радиуса, синим столько же отрезков, которые не являются радиусами.
Домашнее задание: № 113 (рабочая тетрадь).
Урок 39
Взаимное расположение фигур на плоскости
Цели урока: показать учащимся на примерах различные случаи возможного расположения фигур на плоскости: фигуры накладываются одна на другую (пересекаются), расположены отдельно одна от другой (не пересекаются); ввести понятие о пересекающихся и непересекающихся фигурах; совершенствовать вычислительные навыки; развивать умение сравнивать и рассуждать.
Ход урока






