Адамстың интерполяциялық әдісі

Егер (4.3)–теңдіктегі интегралды

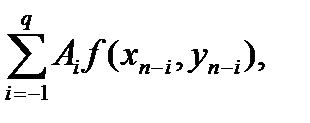(4.16)

қосындымен алмастырсақ, онда

(4.17)

формуласын аламыз.Мұндағы параметірлерін жоғарыда көрсетілген жолдармен анықтаймыз.

Яғни, десек онда

(4.18)

теңдеулер жүйесін аламыз. Бұл теңдеудің

кез келген 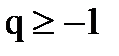болған жағдайда шешуі бар. Немесе параметрлерін былайша да табуға болады:

Ал жіберілген қате –

(4.19)

Енді осы әдістің дербес жағдайларын қарастырайық:

Онда (4.20)

2. Бұл жағдайда (4.21)

3. Онда

(4.22)

4. . Онда

(4.23)

Жалпы Адамстың (4.14) экстрополяциялық формуласы сияқты, Адамстың интерполяциялық формуласын былайша жазуға болады:

(4.24)

мұнда

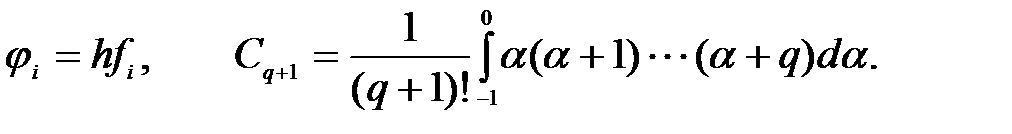
Ал жіберілетін қате –

(4.25)

Адамстың интепрполяциялық әдісі айқындалмаған сызықты емес теңдеу болғандықтан, оның шешуін табу үшін көп жағдайда итерациялық әдістер қолданылады.Сондықтан оны

(4.26)

Түрінде жазу арқылы итерация әдістерін қолдануға ыңғайлы түрге келтіреміз.

Мұнда (4.27)

(4.27) формуладағы көрсетілген аргументтері бойынша белгілі функция.

Енді (4.26) –теңдеуді шешу үшін

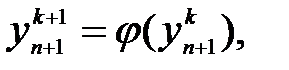(4.28)

Итерациялық әдісін қолдансақ, онда оның жинақталуы үшін 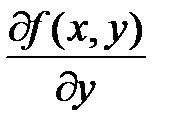аралығында үзіліссіз болуы және бастапқы мән теңдеудің шешуіне жақын болуы жеткілікті.

Екінші ретті дифференциальдық теңдеулерді шешудің сандық әдістері. Шекаралық есебін шешудің сандық әдістері. Қуалау әдісі

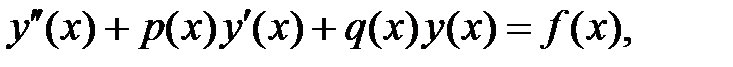(1)

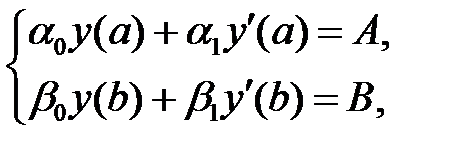(2)

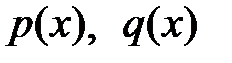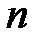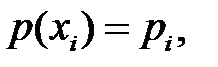
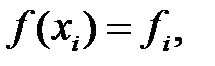
есебін қарастырайық. және функциялары аралығында үзіліссіз болсын. Енді аралығын қадамымен бірдей бөлікке бөлеміз: . аралығының ішкі нүктелері үшін келесі белгілеулерін , енгізейік. Онда (1) теңдеуінің орнына келесі ақырлы айырымды теңдеулерін аламыз

. (*)

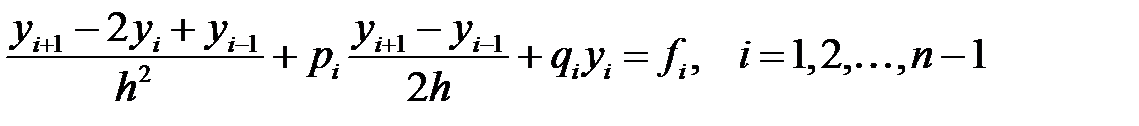Немесе

(3)

мұндағы , , . (4)

және нүктелеріндегі функциясының туындысын бір жақты айырымдылық тундысымен аппроксимациялаймыз

, . (**)

Ендеше (2) шекаралық шартын былайша жазуға болады

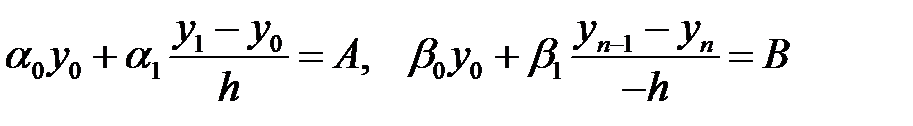. (5)

(3), (5) сызықты жүйесі белгісіздері болатын бірінші дәрежелі 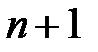теңдеулерден тұрады.

Енді (3) теңдеуінен белгісізін өрнектейік, яғни алатынымыз

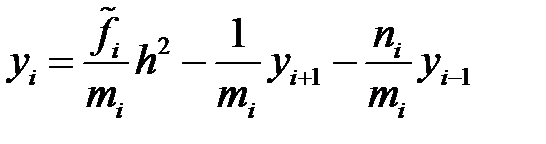. (6)

Айталық, (3) және (5) толық жүйесінің көмегімен, (6) жүйесінен бегісізін (біртіндеп жойып) шығарып тастадық дейік. Онда осы (6) жүйесі келесі түрге келеді

(7)

мұндағы және – кейбер коэффициенттер. Енді (7) формуласынан -ді ((7)-де ) табамыз. Осы өрнекті (3)-ке қойсақ, алатынымыз , мұнан

. (8)

Енді (7) мен (8)-ді салыстырып, мен -ді табатын, рекурренттік формуласын аламыз

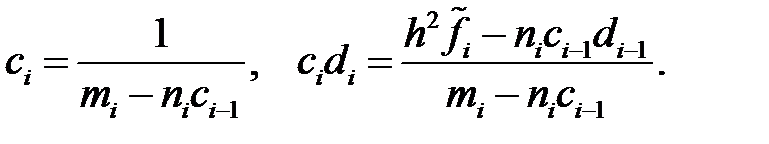Немесе бұдан шығатыны

. (9)

Енді (9)-шы рекурренттік формуласымен мен -ді есептеу үшін мен -ді анықтайық. Ол үшін (5) шекаралық шартының біріншісін келесі түрде жазайық . (5¹)

Енді (7) формуласынан деп алап, алатыннымыз

. (7¹)

(5¹) мен (7¹)-ді салыстыра отырып алатынымыз

. (10)

Ал (9) және (10) формулаларынан біртіндеп мен табамыз. Осы коэффициенттерін табуды – тура жол – дейді.

Кері жол. Алдымен -ді табудан бастайық. Ол үшін (5) -ші шекаралық шартының екіншісін пайдаланып, (7) формуласында десек, келесі екі теңдеуден тұратын жүйе аламыз

(11)

Енді (11)-ден

. (12)

(7) формуласында, яғни 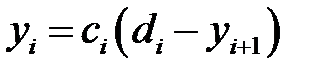формуласында десек, онда барлық мәндерін табамыз.

24. Екінші ретті дифференциальдық теңдеулерді шешудің айырымдылық әдісі.орнықтылығы және қателігі.жинақтылығы.

Дифференциалдық тењдеулері айырымдық ңдістермен шешу – алдымен тор енгізуден басталады. Сондықтан да олар кейде торлық ңдістер деп те аталады. Айырымдық торды тљменде келтірілген мысал арқылы тџсіндірейік.

Айталық, аралыѓында мынадай шекаралық есеп берілсін:

(1.1)

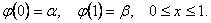(1.2)

Бұл есеп бойынша аралыѓында (1.1) тењдеуін, ал жңне болѓанда, (1.2) шекаралық шарттарын қанаѓаттандыратын функциясын анықтау керек.

Осы қойылѓан есеп џшін аралыѓында айырымдық тор тџрінде енгізіледі. Аныѓырақ айтқанда, аралыѓында бір – бірінен 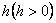қашықтықта жатқан нџктелері алынады. Айырымдық тор паратетріне тңуелді, ал мейлінше љте аз шамаѓа ие болѓан сайын, 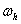торы соншалықты тыѓыз болады. Ңдетте, нџктелерін айырымдық тордыњ тораптары деп атайды.

Айырымдық тор енгізудіњ нңтижесінде аралық тор облысы деп аталатын нџктелер жиынымен алмастырылады, мђндаѓы - тораптар жиыны. Ңдетте (1.1) – (1.2) есебініњ жуық шешімін осы облысында анықтау талап етіледі.

Айталық функциясы (1.1) – (1.2) есбініњ 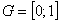обылысында анықталѓан нақты шешімі болсын. Онда

(1.3) сандары осы функциясыныњ сңйкес тораптардаѓы мңндері болады. Бђл жаѓдайда (1.3) сандар жиыны облысында анықталѓан торлық функция деп аталады да арқылы белгіленеді. Ал тараудыњ басында айтылѓандай, (1.1) – (1.2) есебініњ жуық шешімі де облысыныњ тораптарында анықталѓан торлық функция тџрінде анықталады. Ол нџктелеріне сңйкес келетін сандар жиынынан тђрады жңне 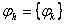деп белгіленеді. Демек, торлық функция џзікті аргументтіњ функциясы, яѓни

Біз бђл жерде екі торлық функцияны қарастырайық: - (1.1) – (1.2) есебініњ тораптарындаѓы дңл шешімі; ал - (1.1) - (1.2) есебініњ тораптарындаѓы жуық шешімі. Жалпы жаѓдайда 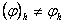, яѓни .

Егер 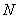саны жоѓарыдан шектелген болса, онда 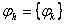жңне торлық функцияларын векторлық функциялар деп қарастыруѓа болады: .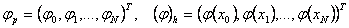

Жоѓарда баяндалѓандай, 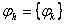- айырымдық тењдеулердіњ шешімі. Ал бђл шешім 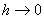жаѓдайда дифференциалдық тењдеулердіњ облысында анықталѓан дңл шешімінде «жақын» болуы тиіс деген талап – табиѓи нңрсе. Енді осы ђѓымды қандай маѓынада тџсіну керек екендігіне тоқтала кетейік. Ол џшін торлық функцияныњ нормасы деген ђѓым енгіземіз.

Анықтама. Егер торлық функциялар жиынында сандық функциясы џшін

1. ;

2. ;

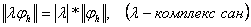3.

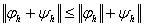
шарттары орындалса, онда шамасы торлық функцияныњ нормасы деп аталады жңне арқылы белгіленеді.

Анықтаманыњ аксиомаларын қанаѓаттандыратын норманы ңр тџрлі жолдармен енгізуге болады. Мңселен

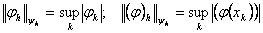(1.4) немесе

(1.5) сандық функциялары норма бола алады. Олар функциялар теориясында белгілі жңне нормаларына сңйкес келеді.

Бђдан ары жңне нормалары (1.4) тџріне енгізілген деп есептейміз.

Норма анықталѓаннан кейін жңне торлық функциялардыњ бір – біріне «жақындыѓын» 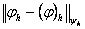нормасыныњ шамасына қарай баѓалаймыз.

25. Ақырғы айырымдар әдісі қуалау әдісін қолданы есеп шығару

Сызықтық дифференциалдық теңдеуді қарастырайық:

(2.4.1)

екі нүктелік сызықтық шекаралық шарттары:

(2.1.2)

мұндағы 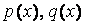және – [ a, b ] аралығында үзіліссіз.

Бұл шекаралық есепті шешудің неғұрлым қарапайым тәсілінің бірі оны ақырғы айырымдық теңдеулер жүйесіне келтіру болып табылады. Ол үшін [ a, b ] кесіндісін h қадаммен тең n бөлікке бөлеміз, мұндағы .

Бөлгіш нүктенің абсциссалары:

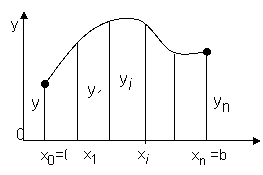
1-сурет.

Ізделінді функцияның және оның туындылары бөлу нүктелеріндегі мәндерін сәйкесінше , және деп белгілейміз. Тағы келесі белгілеулерді енгізейік:

Туындыларды оң біржақты ақырғы айырымдық қатынастармен алмастырсақ, кесіндісінің ішкі нүктелері 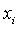үшін жуықтап мына түрге келтіреміз:

(2.4.3)

және шекаралық нүктелері үшін:

және (2.4.4)

деп ұйғарамыз.

(2.4.3) формулаларын қолданып, (2.4.1) дифференциалдық теңдеуін болғанда келесі сызықтық теңдеулер жүйесімен ауыстыруға болады.

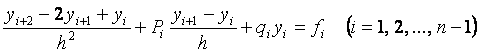(2.4.5)

Одан басқа, (2.1.4) формуласына байланысты (2.1.2) шекаралық шарттар қосымша екі теңдеуді береді:

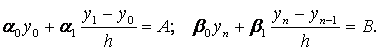(2.4.6)

Сонымен, біз n+1 теңдеуден n+1 белгісізден 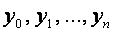тұратын ізделінді функцияның нүктелеріндегі мәндерін беретін сызықтық жүйе алдық. Бұл жүйені шешіп, ізделінді функцияның у мәндерінің кестесін аламыз.

Неғұрлым дәлірек формулаларды симметриялық ақырғы айырымдық қатынастарды қолдану арқылы алуға болады:

(2.4.7)

және шекаралық нүктелердегі туындылары үшін жалпы жағдайда қажеттілігі бойынша (2.4.4) формуласы қолданылады.

Ендеше келесі теңдеулер жүйесін аламыз:

(2.4.8)

26. Қарапайым дифференциалдық теңдеу үшін шекаралық есепті қолданып ақырғы айырымдар әдісімен шешу.

Ақырғы айырымдар әдісінің қолданылуын қарастырайық. Ол үшін төмендегі мысалды шешу мәселесіне жан-жақты тоқталайық.

Мысал: Ақырғы айырымдар әдісімен шекаралық есептің шешімін табу керек:

(2.5.1)

Механикалық тұрғыдан (2.2.1) теңдеулері айнымалы көлденең қимасы бар білеудің иілген моменті үшін дифференциалдық теңдеулерді береді.

2-сурет

Тұрпайы шешім үшін қадам h = 1/2 таңдап аламыз. деп ұйғарып, теңдеудің және шекаралық шарттардың симметриясын ескере отырып, келесі теңдіктерді аламыз:

.

Ендеше бізге тек екі ординатаны ғана және табу керек. деп ұйғарып және туындылар үшін симметриялық формулаларды пайдаланып:

аламыз. Мұндағы .

Сол сияқты болғанда, .

Бұдан шекаралық шартынан жүйе аламыз: .

Бұл жүйені шешсек, =0,967; =0,721.

n - нің үлкен мәндерінде (2.4.5), (2.4.6) жүйелерін шешу қиынға түседі. Бұл жағдайда шекаралық есептің шешімін екі Коши есебінің шешімімен алмастырған дұрыс.

Мысалы, деп ұйғарып,

, (2.5.2)

аламыз. Мұндағы 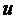Коши есебінің шешімі сияқты табылады.

(2.5.3)

Ал – Коши есебінің шешімі сияқты табылады.

(2.5.4)

С тұрақтысы (2.1.2) шекаралық шарттарына сай келесі мәнді қабылдайды:

(2.5.5)

(2.2.3) дифференциалдық теңдеуін сәйкес ақырғы – айырымдық теңдеумен алмастырып,

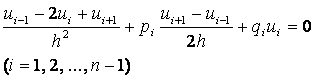
және 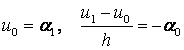аламыз.

Ендеше:

(2.5.6)

Осы үрдістің көмегімен

және табамыз.

Дәл осы сияқты (2.2.4) дифференциалдық теңдеуін ақырғы – айырымдық теңдеумен алмастырып,

және аламыз.

Ендеше:

(2.5.7)

Осы үрдісті қайталай отырып,

және табамыз.

Сонымен бізге (2.2.5) формуласынан С тұрақтысын, одан кейін 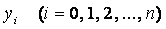мәндерін келесі формуланың көмегімен табуға мүмкіндік туады:

(2.5.8)

Есептеу формуласы ықшамдалады, егер шекаралық шарттар келесі түрде болса:

.

Бұл жағдайда болады да біз

және

Ескерту: -тің жуық мәндерін есептеулерді екі әр түрлі қадаммен жүргізіп дәлдеуге болады.

және – сәйкечсінше h және H қадаммен -тің жуық мәндері болсын.

Қателік қадамның квадратына пропорционал болады десек,

Бұдан, қадамнан тәуелсіз деп есептеп,

Ендеше:

(2.5.9)