МАТЕМАТИКА
Электронный конспект лекций для учащихся заочной формы обучения
Разработчик: Толок Е. И.
Минск 2014
Понятие предела функции в точке
Определение предела функции в точке:
Число А называется пределом функции у = f(x) в точке  , если для любой последовательности (
, если для любой последовательности ( ), все члены которой принадлежат области определения функции, стремятся к
), все члены которой принадлежат области определения функции, стремятся к  , но не совпадают с ним соответствующая последовательность значений функции
, но не совпадают с ним соответствующая последовательность значений функции  стремится к точке А.
стремится к точке А.
 Теорема (необходимое условие существования предела функции в точке):
Теорема (необходимое условие существования предела функции в точке):
Функция у=f(x) имеет предел в точке  тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции f(x) в точке
тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции f(x) в точке  .
.
Теоремы о пределах функции в точке
1° Функция в точке может иметь только один предел.
2° Если  то
то 
3° 
4° 
5° Если 
Пример

Раскрытие неопределенности вида 
Пример.  =
=
Находя предел числителя и знаменателя, получаем  . Говорят, что имеем неопределенность вида
. Говорят, что имеем неопределенность вида  . Раскрыть неопределенность – значит вычислить предел. Для этого предварительно числитель и знаменатель данной дроби раскладываем на множители.
. Раскрыть неопределенность – значит вычислить предел. Для этого предварительно числитель и знаменатель данной дроби раскладываем на множители.
=  =
=  =1.
=1.
Определения бесконечно малой и бесконечно большой величин
Если  в точке а, то функция f(x) называется бесконечно малой(БМФ) в точке а (функция g(x) называется бесконечно большой (ББФ) в точке а)
в точке а, то функция f(x) называется бесконечно малой(БМФ) в точке а (функция g(x) называется бесконечно большой (ББФ) в точке а)
Теорема
Если f(x) – БМФ, то  - ББФ. Если g(x) – ББФ, то
- ББФ. Если g(x) – ББФ, то  - БМФ.
- БМФ.
Пример


Первый замечательный предел

ü Пример

Второй замечательный предел


Пример





 =
=  =
=  .
.
Односторонние пределы
Рассмотрим функцию 
Функция определена в точке  =1.
=1.
По виду графика замечаем, что если точка х приближается к 1, оставаясь меньше 1, т.е. слева, то соответствующие значения функции всё меньше отличаются от 1. Говорят, что 1 – есть предел функции f(x) слева в точке  =1.
=1.
По графику при приближении х к 1 справа, т.е. когда х принимает значения больше 1, соответствующие значения функции как угодно близко приближаются к 2. Говорят, что 2 – предел функции справа в точке  =1.
=1.
Записывают,  и
и 
Такие пределы называются односторонними.
Основные теоремы о непрерывных функциях
Функция у=f(x) называется непрерывной в точке  , если:
, если:
1)функция определена в этой точке;
2)в некоторой окрестности точки  существует предел функции в точке
существует предел функции в точке  , который совпадает со значением функции в этой точке.
, который совпадает со значением функции в этой точке.
Т.е. 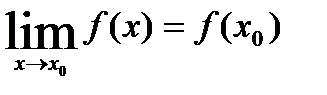
При невыполнении одного из этих условий функция терпит разрыв в точке  .
.
Классификация точек разрыва.
Точка  называется точкой разрыва I рода функции f(x), если в этой точке существуют конечные пределы справа и слева в точке
называется точкой разрыва I рода функции f(x), если в этой точке существуют конечные пределы справа и слева в точке  , не равные друг другу.
, не равные друг другу.

Точка  называется точкой разрыва II рода функции f(x), если в этой точке правый или левый пределы не существуют или являются бесконечными.
называется точкой разрыва II рода функции f(x), если в этой точке правый или левый пределы не существуют или являются бесконечными.

Пример.
Найдите точки разрыва функции f(x) и выясните характер этих точек.
а) 
Функция определена на всей числовой прямой. Найдем односторонние пределы в точке  =1
=1
 ,
, 
Односторонние пределы существуют, конечны, но не равны друг другу, следовательно  =1 – точка разрыва I рода.
=1 – точка разрыва I рода.
б) f(x)= 
Функция определена всюду, кроме точки  = -1, значит
= -1, значит  = -1 – точка разрыва. Установим какого рода.
= -1 – точка разрыва. Установим какого рода.
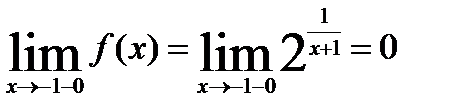 ,
, 
Значит,  = -1 – точка разрыва II рода.
= -1 – точка разрыва II рода.
в) 
Функция определена всюду, кроме точки  = 1, значит
= 1, значит  = 1 – точка разрыва. Установим какого рода.
= 1 – точка разрыва. Установим какого рода.
 ,
, 
Поскольку односторонние пределы в точке 1 бесконечны, то  = 1 – точка разрыва II рода.
= 1 – точка разрыва II рода.
Исследуем функцию в окрестности точки  = 0
= 0
 ,
, 
Односторонние пределы существуют, конечны, равны друг другу, проверим значение функции в точке  =0
=0
f( )=f(0)=
)=f(0)= 
Значение функции совпадает с односторонними пределами, следовательно, в точке  =0 разрыва нет.
=0 разрыва нет.
Асимптоты графика функции
Прямая L называется асимптотой кривой, заданной уравнением y = f(x), если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.
Существуют вертикальные, наклонные или горизонтальные асимптоты.
х = а – вертикальная асимптота, если  - точка разрыва II рода
- точка разрыва II рода
 - наклонная асимптота, если существуют конечные k и b, которые вычисляются по формулам:
- наклонная асимптота, если существуют конечные k и b, которые вычисляются по формулам: 
Если  , то
, то  - горизонтальная асимптота.
- горизонтальная асимптота.
Пример
Найдите асимптоты графика функции 
D(y) = (
Тогда  =0 – точка разрыва. Установим характер разрыва.
=0 – точка разрыва. Установим характер разрыва.

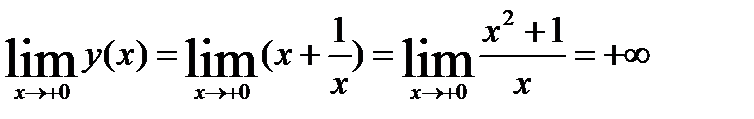
Установили, что  =0 – точка разрыва II рода, х = 0 – вертикальная асимптота
=0 – точка разрыва II рода, х = 0 – вертикальная асимптота
Проверим, имеет ли график наклонные асимптоты вида 

Получили, что  = 1х+0, т.е. у = х – наклонная асимптота.
= 1х+0, т.е. у = х – наклонная асимптота.
Вычисление дифференциала функции
Дифференциалом функции у=f(x) называется произведение производной этой функции  на произвольное приращение аргумента
на произвольное приращение аргумента  :
: 
Дифференциал аргумента равен приращению аргумента:  . Поэтому дифференциал функции равен произведению её производной на дифференциал аргумента:
. Поэтому дифференциал функции равен произведению её производной на дифференциал аргумента: 
Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка:  , т.е. дифференциал второго порядка функции у=f(x) равен произведению второй производной этой функции на квадрат дифференциала аргумента.
, т.е. дифференциал второго порядка функции у=f(x) равен произведению второй производной этой функции на квадрат дифференциала аргумента.
Пример1
Найти дифференциалы первого порядка следующих функций:
а) 

б) 

Применение производной к исследованию функции
Функция y=f(x) называется возрастающей в промежутке  , если для любых
, если для любых  и
и  , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что  <
<  , имеет место неравенство
, имеет место неравенство  .
.
Функция y=f(x) называется убывающей в промежутке  , если для любых
, если для любых  и
и  , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что  <
<  , имеет место неравенство
, имеет место неравенство  .
.
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции y=f(x) характеризуется знаком её производной.
Теорема
Для того чтобы дифференцируемая на  функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы
функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы  для всех х из этого интервала.
для всех х из этого интервала.
Если же для любого х из 
 то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
Из теоремы следует, что для того чтобы функция y=f(x) была постоянной на  , необходимо и достаточно, чтобы выполнялось условие:
, необходимо и достаточно, чтобы выполнялось условие: 
| f´(x)<0 |
| f´(x)=0 |
| f´(x)<0 |
Внутренние точки области определения, в которых производная не существует или равна нулю, называются критическими.
Точка  из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал
из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал  ,
,  , не выходящий из области определения D(f), что для всех х ≠
, не выходящий из области определения D(f), что для всех х ≠  , выполняется неравенство
, выполняется неравенство 
| х0 |
| f(х0) |
| х0 |
| f(х0) |


Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – экстремумы функции.
Следующая теорема показывает, что точки экстремума следует искать среди критических точек функции.
Теорема Ферма
Если точка  - точка экстремума функции y=f(x) и в этой точке существует производная, то
- точка экстремума функции y=f(x) и в этой точке существует производная, то 
Точки перегиба. Необходимое условие точек перегиба
Определение. Точка  из D(f) функции f(x) называется точкой перегиба, если:
из D(f) функции f(x) называется точкой перегиба, если:
1.в этой точке функция непрерывна;
2.существует интервал (а;b),  такой, что на интервалах
такой, что на интервалах  направления выпуклости противоположны, т.е. в точке
направления выпуклости противоположны, т.е. в точке  выпуклость сменяется вогнутостью или наоборот.
выпуклость сменяется вогнутостью или наоборот.
| х0 |
Теорема. (необходимое условие точки перегиба)
Пусть дана функция у=f(x) дважды дифференцируемая на (а;b). Если в точке  график имеет перегиб и существует конечная вторая производная
график имеет перегиб и существует конечная вторая производная  , то
, то  =0.
=0.
Схема исследования функции
1. Найти область определения функции.
2. Четность, периодичность.
3. Исследовать функцию на непрерывность: наличие точек разрыва, их характеристика; асимптоты графика.
4. Найти точки пересечения графика с осями координат.
5. Определить критические точки, промежутки возрастания и убывания функции, а также экстремумы функции.
6. Найти интервалы выпуклости и вогнутости, точки перегиба.
7. Построение графика.

Пример.
Построить график функции 
1. 
2.Функция не является ни чётной ни нечётной; кроме того, она не является периодической.
3.Функция непрерывна в области определения.
х=2 – точка разрыва
Исследуем функцию в окрестности точки х=2


Следовательно, х=2 – вертикальная асимптота
Найдем наклонные: 

 является наклонной асимптотой графика функции.
является наклонной асимптотой графика функции.
4. (0;  ), (-1;0) – точки пересечения с координатными осями.
), (-1;0) – точки пересечения с координатными осями.
5. 
 - критические точки.
- критические точки.
+ - - +
| -1 2 5 |

Найдем экстремумы функции:

6. 
Вторая производная в нуль не обращается на всей области определения функции.
- +
7.Построим график функции:
| -1 |
Неопределенный интеграл и его свойства
Определение
Пусть функции f(x) и F(x) определены на (a;b). Если функция F(x) имеет производную на (a;b) и для всех х из этого интервала выполняется равенство  (1), то функция F(x) называется первообразной для функции f(x) на интервале (a;b).
(1), то функция F(x) называется первообразной для функции f(x) на интервале (a;b).
Теорема
Если определенная на интервале (a;b) функция f(x) имеет на нем хотя бы одну первообразную F(x), то она имеет на этом интервале бесконечное множество первообразных, элементами которого являются функции F(x)+С,  и только они.
и только они.
Пример.
Каждая из функций  , где С – произвольное действительное число, является первообразной для функции
, где С – произвольное действительное число, является первообразной для функции  на R.
на R.
Из теоремы очевидно, что при любом действительном С график функции F(x)+С получается из графика функции F(x) путем параллельного переноса последнего на величину С вдоль оси ординат.
Таким образом, теорема утверждает, что вся совокупность графиков первообразных функции f(x) получается из одного из них путем всевозможных параллельных переносов этого графика вдоль оси ординат.
Определение.
Совокупность всех первообразных функций для функции f(x) на интервале (a;b) называется неопределенным интегралом от функции f(x) на этом интервале.
Обозначается: 
Функция f(x) называется подынтегральной, знак  называется знаком интеграла, а выражение, записываемое справа от него: f(x)dx – подынтегральным выражением.
называется знаком интеграла, а выражение, записываемое справа от него: f(x)dx – подынтегральным выражением.
Нахождение неопределенного интеграла от функции f(x), заданной на некотором интервале 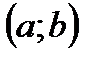 , называется интегрированием.
, называется интегрированием.
В соответствии с определением и теоремой выше, можно записать: 
Если первообразная (а значит, и неопределенный интеграл) для функции f(x) на интервале (a;b) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных.
Пусть F(x) – некоторая первообразная на (a;b), т.е. для любого х из (a;b) выполняется  , тогда
, тогда  (3)
(3)
Функция  одна из первообразных для функции
одна из первообразных для функции  на всей числовой прямой, т.е.
на всей числовой прямой, т.е. 
Функция  является одной из первообразных для функции
является одной из первообразных для функции  на (-1;1), значит
на (-1;1), значит  на (-1;1)
на (-1;1)
Основные свойства неопределенного интеграла
1° 
2° 
Из (2) следует 
3° 
Это свойство следует из (2) и (3)
4° 
Для доказательства этого свойства достаточно показать, что если F(x) и G(x) первообразные функций f(x) и g(x) соответственно, то функция  является первообразной для функции
является первообразной для функции 

5° 

Эти свойства и таблица интегралов позволяет вычислить многие интегралы от несложных выражений.
Таблица неопределенных интегралов
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
Характеристика методов интегрирования
Правило подведения под знак дифференциала.
Правило основано на следующем очевидном утверждении, которое следует из инвариантности формы первого дифференциала: если  , где х – независимая переменная, то верно и равенство
, где х – независимая переменная, то верно и равенство  , где u=u(x) – функция от х.
, где u=u(x) – функция от х.
Например,  ит.п.
ит.п.
На практике, исходный вид вычисленных интегралов обычно имеет другую форму:  и сведение их к табличным интегралам обеспечивается равенством
и сведение их к табличным интегралам обеспечивается равенством 
То есть, используется таблица производных, прочитанная справа-налево. В первом случае под знак дифференциала внесли cosx, во-втором -  .
.
Примеры.
 . Здесь воспользовались
. Здесь воспользовались 




 , так как
, так как 


Следует отметить, что рассмотренное правило является частным случаем более общего правила замены переменной.
Правило замены переменной.
Утверждение, на котором основывается предыдущее правило, но записанное в виде
 , где
, где  - дифференцируемая функция, множество значений которой является областью определения функции
- дифференцируемая функция, множество значений которой является областью определения функции  . Естественно, как и ранее, мы предполагаем существование всех указанных интегралов. Из этой формулы следует и смысл замены переменной: функцию
. Естественно, как и ранее, мы предполагаем существование всех указанных интегралов. Из этой формулы следует и смысл замены переменной: функцию  стараются подобрать так, чтобы подынтегральное выражение
стараются подобрать так, чтобы подынтегральное выражение  , в полученном после преобразований интеграле, было проще исходного.
, в полученном после преобразований интеграле, было проще исходного.
Примеры.



 .
.
Правило интегрирования по частям.
Дифференциал произведения двух функций  и
и  определяется формулой
определяется формулой  . Перепишем равенство в виде
. Перепишем равенство в виде  и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:
и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:

С помощью этой формулы обычно вычисляются интегралы от функций представляющих произведение многочлена на  причем в первых трех случаях за
причем в первых трех случаях за  обозначают многочлен, а в последнем
обозначают многочлен, а в последнем  . Поскольку в правой части формулы вместо функции
. Поскольку в правой части формулы вместо функции  появляется дифференциал этой функции
появляется дифференциал этой функции  , то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция
, то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция  выбрана, оставшееся под интегралом выражение обозначаем
выбрана, оставшееся под интегралом выражение обозначаем  , тогда сама функция
, тогда сама функция  .
.
Примеры.
a) 

b) 

Понятие определенного интеграла.
Рассмотрим функцию  определенную и непрерывную на некотором отрезке
определенную и непрерывную на некотором отрезке  числовой прямой. Разобьем
числовой прямой. Разобьем  на n отрезков
на n отрезков 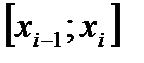 длины
длины  точками
точками  . На каждом i- том отрезке берем произвольную точку
. На каждом i- том отрезке берем произвольную точку  . Вычисляем значение функции
. Вычисляем значение функции  в каждой из этих точек и умножаем его на длину соответствующего отрезка
в каждой из этих точек и умножаем его на длину соответствующего отрезка  . После чего суммируем по всем отрезкам
. После чего суммируем по всем отрезкам  .
.
Полученное выражение называют интегральной суммой. Понятие интегральной суммы играет определяющую роль в определении всех интегралов.
Если предел интегральной суммы при стремлении к нулю максимальной длины  не зависит ни от способа разбиения отрезка
не зависит ни от способа разбиения отрезка  на промежутки
на промежутки 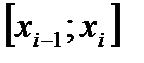 , ни от способа выбора точек
, ни от способа выбора точек  в каждом из этих промежутков, то он называется определенным интегралом от функции
в каждом из этих промежутков, то он называется определенным интегралом от функции  в пределах от а до b и обозначается:
в пределах от а до b и обозначается:  .
.
Свойства определенного интеграла.
I. 
II. 
III. 
IV. 
V. 
VI. Если  для всех
для всех  , то
, то 
VII.  , если a<b.
, если a<b.
VIII. Теорема о среднем. Если f(x) непрерывна на  , то существует точка
, то существует точка  , такая что
, такая что 
Формула Ньютона-Лейбница
Пусть  непрерывна на
непрерывна на  и переменная
и переменная  . Тогда совокупность всех первообразных для этой функции можно выразить формулой
. Тогда совокупность всех первообразных для этой функции можно выразить формулой  . Легко видеть, что
. Легко видеть, что  . Откуда, заменив переменную интегрирования снова на х, получим формулу Ньютона –Лейбница:
. Откуда, заменив переменную интегрирования снова на х, получим формулу Ньютона –Лейбница:

Для того чтобы вычислить определенный интеграл, прежде всего вычисляется одна из первообразных F(x), затем вычисляется значение этой функции в точке b и вычитается её значение в точке а.
Пример.
Вычислить 
 .
.
Геометрический смысл определенного интеграла
Часть плоскости, ограниченная кривой у=f(x), осью Ох и прямыми х=a, х=b называется криволинейной трапецией.
| а |
| b |
| f(x) |
| x |
| y |
Площадь криволинейной трапеции вычисляется при помощи определенного интеграла.

В случае, когда криволинейная трапеция, ограниченная кривой у=f(x), осью Ох и прямыми х=a, х=b, лежит под осью Ох, площадь находится по формуле:

 а а
|
| b |
 x x
|
| y |
Если фигура, ограниченная кривой у=f(x), осью Ох и прямыми х=a, х=b, расположена по обе стороны от оси Ох, то:

 а а
|
| b |
 x x
|
| y |
 с с
|
Пусть, наконец, фигура S ограничена двумя пересекающимися прямыми кривыми  , где
, где  и прямыми х=a, х=b,тогда площадь находится по формуле:
и прямыми х=a, х=b,тогда площадь находится по формуле:

 а а
|
| b |
 x x
|
| y |
 f1(x) f1(x)
|
 f2(x) f2(x)
|






