Дискретная математика – раздел математики, в котором изучаются свойства структур конечного характера.
Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно.
Отрицанием высказывания A называется такое высказывание 
, которое будет истинно тогда и только тогда, когда высказывание A – ложно.
Таблица истинности:
| A |
|
| и | л |
| л | и |
Конъюнкцией двух высказываний A и B называется новое высказывание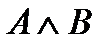 
, которое истинно тогда и только тогда, когда оба высказывания A и B – истинны.
Таблица истинности:
| A | B |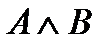
|
| л | л | л |
| л | и | л |
| и | л | л |
| и | и | и |
Дизъюнкцией двух высказываний A и B называется новое высказывание 
, которое истинно тогда и только тогда, когда хотя бы одно из выска-зываний A или B – истинно.
Таблица истинности:
| A | B | 
|
| л | л | л |
| л | и | и |
| и | л | и |
| и | и | и |
Импликацией двух высказываний A и B называется новое высказывание 
, которое ложно тогда и только тогда, когда A – истинно, а B – ложно.
Таблица истинности:
| A | B |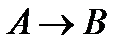 
|
| л | л | и |
| л | и | и |
| и | л | л |
| и | и | и |
Эквивалентностью двух высказываний A и B называется новое высказывание 
, которое истинно тогда и только тогда, когда A и B одновременно истинны или одновременно ложны.
Таблица истинности:
| A | B | 
|
| л | л | и |
| л | и | л |
| и | л | л |
| и | и | и |
Порядок выполнения логических операций:
- отрицание,
- конъюнкция,
- дизъюнкция,
- импликация,
- эквивалентность.
Если есть скобки, то сначала выполняются операции в скобках.
Правило суммы: Если объект A можно выбрать m способами, а объект B - n способами, то объект A или B можно выбрать m+ n способами.
Правило произведения: Если объект A можно выбрать m способами, а после каждого выбора другой объект B можно выбрать n способами, то пару объектов A и B можно выбрать 
способами.
Пусть имеется множество, содержащее n элементов. Размещением из n элементов по m элементов называется любое упорядоченное подмножество данного множества, содержащее m элементов.
Число всевозможных размещений из n элементов по m обозначается: 
.
= 
, где n! = 1·2·3·…· n.
Перестановки - это размещения из n элементов по n.
Число перестановок обозначается: 
. Находится число перестановок из n элементов по формуле: 
= n!.
Пусть имеется множество, содержащее n элементов. Сочетанием из n элементов по m элементов называется любое подмножество данного мно-жества, содержащее m элементов.
Число всевозможных сочетаний из n элементов по m обозначается: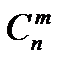 
.
= 
.
Тема 9. Теория вероятностей и математическая статистика
