Основні правила диференціювання

Основні теореми про границі функцій

Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому
;
.
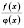Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює
.
Теорема 3. Якщо при функція має границю A, то ця границя єдина.

11) Гіпербола. Означення. Множина точок площини, для яких модуль різниці відстаней від двох заданих точок, що називаються фокусами, є величиною сталою, яка дорівнює 2 а і менша за відстань між фокусами, називається гіперболою.

 

Канонічне рівняння гіперболи має вигляд:

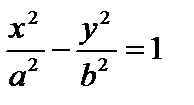, де b ² = c ² – a ².

Парабола. Означення. Множина то­чок площини, що містяться на одна-
ковій відстані від даної точки фокуса
і даної прямої, яка не проходить че-
рез фокус і називається директрисою, є парабола.

або у ² = 2 рх

— канонічне рівняння параболи, коли e = 1. Парабола симетрична осі Ох, проходить через початок системи координат.

12 Означення. Функція називається неперервною в точці якщо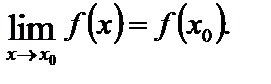

Властивості неперервних функцій

Теорема 1. Якщо функції і неперервні у точці то у цій точці будуть неперервними функції ; в останньому випадку за умови, що

Теорема 2. Якщо функція — неперервна для а функція — неперервна для і значення функції то складна функція — неперервна для

Теорема 3 (Коші). Якщо функція неперервна на закритому проміжку і на кінцях проміжку набуває значення різних знаків (наприклад ), тоді на відкритому проміжку існує така точка х = с, що

Методика дослідження функції на неперервність.

1. Знайти область визначення функції D(y).

2. Визначити скінченні граничні точки D(y) і обчислити односторонні границі функції у цих точках.

3. Зробити висновок про характер точок розриву (якщо вони є) і побудувати графік функції поблизу цих точок

13) Означення. Похідною функції за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

Операція знаходження похідної називається диференціюванням цієї функції.

Геометричний зміст похідної — похідна чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х.

Механічний зміст похідної

Припустимо, що точка М рухається прямолінійно нерівномірно по деякій прямій лінії, яку візьмемо за вісь Ох Рух точки відбувається за законом х = f (t), де х — шлях; t — час. Знайдемо швидкість точки М у да-
ний момент часу t (миттєва швидкість).

Нехай точка М у момент t перебувала на відстані х від початкової точки М ₀, а в момент часу 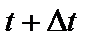точка опинилася на відстані 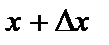від початкової точки й зайняла положення М ₁. Отже, час t набув приросту , а шлях х — приросту . Середня швидкість руху точки М за час описується формулою .

Основні правила диференціювання

Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то .