Лабораторная работа № 18.
Определение радиуса кривизны линзы и ее фокусного расстояния
1. Цель работы: закрепление теоретических знаний по теме 4.1. “Элементы геометрической и электронной оптики”,
приобретение практических навыков работы с линзовыми элементами,
изучение методики расчетов радиусов кривизны и фокусных расстояний реальных линз
2. Порядок подготовки к выполнению работы изучить тему и материал лабораторной работы
3. Порядок выполнения лабораторной работы дан в описании
4. Подведение итогов выполнения работы
предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений
5. техника безопасности при выполнении лабораторной работы стандартная
Оборудование: прибор для измерения радиуса кривизны, линейка, штангенциркуль, световая пушка, лампа накаливания, линзы, экран
Упражнение 1
Измерение радиуса кривизны линзы
Цель работы: научиться пользоваться прибором для измерения кривизны поверхности; проверить основные законы геометрической оптики
Используем прибор для измерения радиуса кривизны R сферических поверхностей. База прибора (сторона правильного треугольника, лежащего в основании) составляет а = 34 мм. r – радиус окружности, в которую вписан этот треугольник. R – радиус кривизны сферической поверхности. h – измеряемая стрелка (высота сферического сегмента с кругом радиуса r в основании)
Дано: а = 34 мм. Тогда r = 
= 
(рис.1); R2 = (R - h)2 + r2 (рис.2);
R = 
; ΔR = 
.
Для определения фокусного расстояния используем формулу
1/f = [(n - 1)(1/R1 – 1/R2)] + (n - 1)2 (d/n) (1/R1 R2),
задающую фокусное расстояние эквивалентной толстой линзы толщиной d в параксиальном приближении (знаки R1и R2 определяются направлением отсчёта от оптического центра линзы (см. рис.)). Показатель преломления n берется как отношение показателя преломления материала линзы к показавтелю преломления окружающей среды.
r1 > 0 r2 < 0
 |
Рис. 1 Рис. 2
Упражнение 2 Световая пушка
Световая пушка –оптический прибор, позволяющий формировать световые пучки с малой угловой расходимостью. В элементарном курсе оптики показывается, что точечный источник, помещенный в фокус положительной линзы, формирует световой пучок с нулевой расходимостью. Однако это справедливо для идеальной оптической системы в параксиальном приближении. Кроме того, создать точечный источник большой яркости весьма сложно.
Можно было бы для указанной цели использовать параболический рефлектор. Он мог бы перехватить гораздо больший световой поток от источника, чем линза. Однако тогда пришлось бы использовать глубокий параболоид с фокусом близким к вершине. Это затрудняет теплообмен и снижает стойкость отражающего покрытия. Если в параболоид поместить источник конечных размеров, то расходимость светового пучка сильно возрастает.
Световая пушка должна обеспечивать на экране равномерно освещенное пятно с резко очерченными краями. Она применяется в сценическом (театральном) освещении, как имитатор солнечного освещения и, разумеется. она может работать как прожектор направленного света.
Рассмотрим кратко основные принципы построения световой пушки.
Расходимость пучка лучей, прошедших от источника с диаметром a
через оптическую систему с фокусным расстоянием f обусловлена следующими факторами:
- конечностью размеров тела накала источника:
(1)
(предполагается а<<f);
- дифракционной расходимостью:
(2)
здесь λ - длина волны (0,55 мкм), D – диаметр объектива;
- геометрическими погрешностями (отклонением формы линз от расчетной):
, (x ̴ 
¸ 
), (3)
- несоосностью оптических элементов:
αА = 
» k2 
(4)
m – увеличение, Δ - несоосность оптики, k1, k2 – постоянные для данной оптической схемы величины. Обычно полагают, что Δ увеличивается пропорционально D и тогда величина α А постоянна.
Полная расходимость пучка в результате воздействия всех этих факторов:
(5)
Таким образом, реальные пути уменьшения расходимости состоят в том, чтобы иметь источник с минимальными габаритами a и большой габаритной яркостью; также нужно стремиться использовать длиннофокусные оптические системы. Эти требования во многом противоречивы.
Источники света с короткой дугой не стабильны в силу самой природы дугового разряда. В них порядок величины а ~1 мм. С другой стороны, увеличение фокусного расстояния при заданном диаметре D объектива снижает световой поток через систему в силу геометрического фактора:
(6)
Е0 – освещенность на выходе при фокусном расстоянии f0.
Таким образом, уменьшить α1 возможно, применяя малогабаритные лампы накаливания с плоским телом накала, ориентированным перпендикулярно оптической оси системы при умеренных фокусных расстояниях f.
Другой реальный путь уменьшения расходимости пучков связан с уменьшением аберраций в оптической системе.
Пусть объектив представляет собой одиночную собирающую линзу нулевой толщины. Тогда радиус ρ пятна сферической аберрации находится по формуле:
ρ = k R0 3,
(7)
где R0 – радиус линзы, R1 – радиус кривизны передней поверхности линзы,
R2 < 0 – радиус кривизны задней поверхности, n – показатель преломления. Такой сферической аберрации соответствует угол расходимости:
(8)
Сферическая аберрация в обычной линзе порождает ореолы вокруг светлых мест изображения объектов в монохроматическом свете.
Аберрация минимальна, когда:
(9)
Если подойти с энергетической точки зрения, то нужно учесть, что 70% энергии, находящейся в пятне рассеяния радиуса ρ1, сконцентрировано в круге с радиусом ρ0 = 0,6 ρ1.
Кроме того, сферическая аберрация имеет перетяжку, радиус которой
ρ1 = 
ρ0. Учет этих факторов не меняет порядка величины угла расхо-димости.
Если учесть конечную толщину t линзы, то мы получим следующее выражение для фокусного расстояния:
f = 
(10)
Если f0 – фокусное расстояние линзы нулевой толщины, то увеличение Δƒ Фокусного расстояния линзы толщины t равно:
(11)
Эту поправку на фокусное расстояние необходимо учесть в (8). Для линзы с минимальной сферической аберрацией и комой соотношение между радиусами кривизны имеет вид:
(12)
Таким образом, на основе простой линзы невозможно добиться приемлемой параллельности пучка, поскольку ее аберрация тем больше, чем больше радиус линзы. Увеличение радиуса необходимо для перехвата большего потока энергии, идущего от источника.
Вторым существенным моментом является возможность уменьшить хроматическую аберрацию простыми средствами.
Изменение фокусного расстояния δƒ тонкой линзы в зависимости от изменения показателя преломления в соответствии с (10) при t =0:
(13)
По Аббе, относительная дисперсия определяется на трех длинах волн
(
= 4861 А0,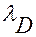 
= 5893 А0, 
= 6563 А0 ) как
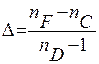(14)
Параметр Аббе Δ имеет простой физический смысл. Он равен расстоянию между красным и синим изображениями, деленному на фокусное расстояние линзы.
Произведением ахроматизацию для двух волн с помощью двух различных тонких линз, находящихся на расстоянии друг от друга. Для фокусного расстояния такой системы имеем:
(15)
Отсюда:
(16)
Проведем ахроматизацию для линий С и F. Тогда из (13) и (14):
(17)
Если линзы соприкасаются, из (17) следует при l = 0:
(18)
Используя (15), имеем:
(19)
Но теперь, в случае линзы-склейки, f1 и f2 зависят от трех радиусов кривизны. Выберем один из них так, чтобы минимизировать сферическую аберрацию. Это и будет оптимальная линза – склейка.
Соотношение (16) предусматривает и другой способ ахроматизации. Можно делать линзы из одинакового стекла Δ1 = Δ2, но разнести их на расстояние l:
(20)
Из (17) следует ахроматичность системы. Однако второй способ менее приемлем, т.к. требует более тщательной сборки.
Таким образом, на основе существующей элементной базы, доступных стабильных источников света и простых линз, легко можно достичь расходимости световых пучков менее расходимости солнечных лучей (30 угловых минут). Дешевизна таких устройств в сравнении с автоколиматорами и лазерами, простота юстировки, высокая надежность делает их перспективным и для малогабаритных переносных приборов.
Технические характеристики нивелиров
| Тип ниве лира | Увеличение | Угол поля зрения | L,м | φ, с | Цена деления уровня, с | Δх, мм/км хода | Масса, кг | |
| Цилиндри ческого | Круглого | |||||||
| НА-1 | 10 20′ | 17 - 23 | 7 - 15 | - | 1,8 | |||
| НГ | 10 | 4,5 | 17 - 25 | 1 – 15 | - | 2,25 | ||
| НА-3 | 10 | 3,6 | 4 на 0,8 мм | - | 6,2 | |||
| НТ | 10 30′ | 1,5 | - | - | ||||
| Н2 | 39,7 | 55′ | - | - | 5,8 | |||
| Н3 | 30,5 | 10 20′ | - | |||||
| НВ-1 | 30,5 | 10 20′ | 17 – 23 | - | 3 - 4 | 1,8 | ||
| НСМ-2А | 30,5 | 10 20′ | 8 (± 2,0) | - | 3 - 4 | |||
| НЗК-1 | 10 20′ | 10 (± 1,0) | - | 3 – 4 | 2.4 | |||
| НС-3 | 10 15′ | 4,5 | - | 2,1 | ||||
| Н1 | 00 50′ | 4,2 | 2,6 | 4 на 0,8 мм | - | 0,5 | 6,9 |
L - минимальное расстояние нивелирования, Δх - среднеквадратичная ошибка, φ - разрешающая способность.
Технические характеристики теодолитов
| Тип теодоли та | F, мм | к | L, м | Точ ность отсчета, мин | Цена деления уровня на алидаде, с | Δх, с | Масса, кг | |
| горизонтального круга | вертикального круга | |||||||
| ТБ-1 | 249,7 | 22,5 | 1,2 | 5,1 | ||||
| ОТ-10* | 25,3 | 1,5 | 40 – 60 | 15 – 20 | - | 6,3 | ||
| ТТП* | 25,2 | 2,0 | 35 -55 | 25 - 35 | 3,4 | |||
| ТОМ | 142,5 | 2,0 | 0,5 | 1,9 | ||||
| ТЗО | 1,0 | 0,5 | 2,0 | |||||
| Т20 | 0,9 | 0,2 | 2,2 | |||||
| ОМТ-30 | 1,0 | 0,5 | 3,2 | |||||
| Т-10 | 1,5 | 0,1 | 3,6 | |||||
| Т-5 | 2,0 | 0,1 | 3,6 | |||||
| Т-2 | 1,5 | 5,2 | ||||||
| ОТ-02 | 24, 30, 40 | 5,0 | 0,2 | - | 11,0 |
F – фокусное расстояние объектива, к – увеличение зрительной трубы, L - минимальное расстояние визирования, Δх - среднеквадратичная ошибка одного приема, * - масса прибора с треножником
Типы и основные параметры визуальных автоколлиматоров
| Тип | Цена деления | Предел измерения по отсчетному устройству | Предел допусукаемой погрешности Δ = φ′′/100 | D, мм | k | |
| Минут ной шкалы | Секундной шкалы, φ | |||||
| АК-0,25 | 0,25′ | 0,25′′ | 6′ | 0,25′′ ± Δ | ||
| АК-0,5 | 0,5′ | 0,5′′ | 10′ | 0,5′′ ± Δ | ||
| АК-1 | 1′ | 1′′ | 12′ | 1′′ ± Δ | ||
| АК-5 | 2′ | 5′′ | 30′ | 5′′ ± Δ | ||
| АК-30 | 0,5′ | 30′ | ± 20′′ | |||
| МГА | 0,5′ | 1′′ | 6′ | 1′′ ± Δ |
D - диаметр входного отверстия, k - общее увеличение
Расходимость излучения некоторых лазеров (в угловых минутах)
| Тип | φ′ | Тип | φ′ | Тип | φ′ |
| ЛГ- 78 | ЛГ- 75 | ЛГ- 126 | |||
| ЛГ- 55 | ЛГ- 38 | ЛГ- 31 | |||
| ЛГ- 44 | ЛГ- 36А | ЛГ- 63 | |||
| ЛГ- 32 | ЛГН- 207А | 5,33 | ЛГ- 207В | 7,40 |
Упражнение 3.
Определение фокусного расстояния собирательной линзы
Описание прибора. На расположенной горизонтально оптической скамье могут перемещаться на ползунках следующие приборы: линза, экран со шкалой, зрительная труба и электрическая лампочка в специальном осветителе. В передней стенке осветителя имеется вырез, освещаемый находящейся внутри него лампочкой. Освещённый прямоугольник этого выреза играет роль объекта (предмета), изображение которого получается с помощью изучаемых линз. Для повышения точности фокусировки изображения в вырезе натянута сетка, перед которой для ослабления хроматической аберрации помещен светофильтр (обычно окрашенная в красный цвет пленка). Ячейки центральной части сетки можно сфокусировать гораздо точнее, чем края выреза.
Все эти приборы устанавливаются так, чтобы центры их лежали на одной высоте, плоскости экранов были перпендикулярны к длине оптической скамьи, а ось линзы – ей параллельна. Расстояния между приборами отсчитываются по шкале линейки (масштабу), расположенной вдоль скамьи, при помощи указателей, укрепленных на ползунках.
Определение фокусного расстояния собирательной линзы производится следующими способами.
Способ 1. Определение фокусного расстояния по расстоянию предмета и его изображения от линзы. Если обозначить буквами a и b расстояния предмета и его изображения от линзы, то фокусное расстояние последней выразится формулой
или f = 
(1 - 2)
(эта формула справедлива только в том случае, когда толщина линзы мала по сравнению с a и b).
Измерения. Поместив экран со шкалой на достаточно большом расстоянии от осветителя, ставят линзу между ними и передвигают ее до тех пор, пока не получат на экране отчетливого изображения выреза в осветителе и натянутой в нем сетки. Отсчитав по линейке, расположенной вдоль скамьи, положение линзы, экрана и сетки, передвигают ползунки с осветителем и экраном в другое положение и вновь отсчитывают соответствующее положение линзы и всех приборов на линейке.
Ввиду неточности визуальной оценки резкости изображения, измерения рекомендуется повторять не менее десяти раз. Кроме того, в данном способе полезно проделать часть измерений при увеличенном, а часть при уменьшенном изображении сетки.
Из каждого отдельного измерения по формуле (2) вычисляют фокусное расстояние линзы и из полученных результатов находят его среднее арифметическое значение.
Для того чтобы убедиться, что форма изображения не зависит от величины и формы отверстия линзы, рекомендуется перед линзой или за ней помещать поочередно различные диафрагмы из прилагаемого набора (щель, кольцо, полукруг и т.п.) и проследить их влияние на изображение. Проследить также за влиянием диафрагмирования линзы на резкость даваемого ею изображения.
Способ 2. Определение фокусного расстояния по величине предмета и его изображения и по расстоянию последнего от линзы. Обозначим величину предмета l, величину его изображения L и расстояние их от линзы - соответственно через a и b. Эти величины связаны между собой известным соотношением
Определяя отсюда a (расстояние от предмета до линзы) и подставляя его в формулу (1), легко получить выражение f через эти три величины
f = b 
(3)
Измерения. Ставят линзу между экраном и предметом так, чтобы на экране со шкалой получилось сильно увеличенное отчетливое изображение выреза в осветителе и сетки, и отсчитывают положения линзы и экрана. Измеряют при помощи линейки величину предмета и величину его изображения на шкале экрана. Измерив расстояния от изображения до линзы, находят фокусное расстояние линзы по формуле (3).
Изменяя расстояние от плоскости сетки до экрана, повторяют опыт несколько раз.
Способ 3 (Бесселя). Определение фокусного расстояния по величине перемещения линзы. Если расстояние от предмета до изображения, которое обозначим через A, более 4f, то всегда найдутся два таких положения линзы, при которых на экране получается отчетливое изображение предмета: в одном случае уменьшенное, в другом – увеличенное (рис. 291).
Нетрудно видеть, что при этом оба положения линзы будут симметричны относительно середины расстояния между предметом и изображением. Действительно, воспользовавшись уравнением (2), можно написать для первого положения линзы (рис.291).
f = 
и для второго положения
f = 
Приравняв правые части этих уравнений, найдем
x = 
Подставив это значение x в выражение A – e – x, легко найдем, что
A – e – x =
т.е. что действительно оба положения линзы находятся на равных расстояниях от предмета и изображения и, следовательно, симметричны относительно середины расстояния между предметом и изображением.
Чтобы получить выражение для фокусного расстояния, рассмотрим одно из положений линзы, например, первое; для него расстояние от предмета до линзы
a =
а расстояние от линзы до изображения
b = 
Подставляя эти величины в формулу (2), найдем
f = 
(4)
Этот способ является принципиально наиболее общим и пригодным как для толстых, так и для тонких линз. Действительно, когда в предыдущих случаях пользовались для расчетов величинами a и b, то подразумевали отрезки, измеренные до центра линзы; на самом же деле следовало эти величины измерять от соответствующих главных плоскостей линзы, определение положения которых довольно затруднительно. В описываемом же способе эта ошибка исключается благодаря тому, что в нем измеряется не расстояние от линзы, а лишь величина ее перемещения.
Измерения. Установив осветитель и экран на расстоянии А > 4f (ориентировочно значение f берут из предыдущих опытов), помещают линзу между ними и, передвигая ее, добиваются получения на экране вполне отчетливого изображения предмета, например увеличенного. Отсчитав по шкале соответствующее положение линзы, сдвигают ее в сторону и вновь устанавливают. Эти измерения производят несколько раз.
Передвигая линзу, добиваются получения второго отчетливого изображения предмета – уменьшенного и вновь отсчитывают положение линзы по шкале. Повторяют опыт и измерения несколько раз.
Измерив расстояние А между экраном и сеткой осветителя, а также среднее значение перемещения е, вычисляют фокусное расстояние линзы по формуле (4).
Способ 4. определение фокусного расстояния посредством зрительной трубы. Как известно, лучи выходящие из фокуса линзы, пройдя ее, идут параллельно оптической оси линзы. На этом свойстве линз основан четвертый способ.
Измерения. Устанавливают зрительную трубу на бесконечность путем наводки ее на достаточно удаленный предмет. Ставят трубу на оптическую скамью и помещают перед ее объективом исследуемую линзу, а за ней осветитель.
Передвигая линзу, устанавливают ее так, чтобы в трубе получилось совершенно отчетливое изображение сетки, и измеряют расстояние от сетки до линзы, которое и будет равно искомому фокусному расстоянию.
Упражнение 4.
Определение фокусного расстояния рассеивающей линзы.
Описание прибора. Укрепленные на ползунках рассеивающая собирательная линзы, полупрозрачный экран и осветитель размещают вдоль оптической скамьи и устанавливают согласно тем же правилам, как и в упражнении 3.
Измерение фокусного расстояния рассеивающей линзы производится следующими способами.
Способ 1. Определение фокусного расстояния по расстоянию предмета и его изображения от линзы. Если на пути лучей, выходящих из точки А и сходящихся в точке D после преломления в собирательной линзе В поставить рассеивающую линзу С так, чтобы расстояние CD было меньше ее фокусного расстояния, то изображение точки А удалится от линзы В. Пусть, например, оно переместится в точку Е. В силу оптического принципа взаимности мы можем теперь мысленно рассмотреть лучи света, распространяющиеся из точки Е в обратную сторону. Тогда точка D будет мнимым изображением точки Е после прохождения лучей через рассеивающую линзу С.
Обозначая расстояния ЕС буквой а, DC – через b и замечая, что f и b имеют отрицательные знаки, получим согласно формуле (1)
и, следовательно, f = 
(5-6)
Измерения. На оптической скамье размещают осветитель, собирающую линзу и полупрозрачный экран. Передвигая экран, получают на нем отчетливое изображение сетки осветителя. Сделав отсчет этого положения экрана на шкале оптической скамьи, сдвигают экран в сторону и вновь находят изображение сетки. Таких установок и отсчетов делают до десяти и берут из них среднее арифметическое. Это дает положение точки D.
Отодвинув экран влево, ставят на скамью между найденным выше положением экрана и собирательной линзой исследуемую линзу и вновь находят отчетливое изображение сетки. Отсчитывают по шкале оптической скамьи положение линзы (или экрана) и, сдвигая ее (или экран), повторяют установку и отсчеты до десяти раз; из полученных результатов берут среднее.
Отыскав несколько раз второе положение экрана (точку Е), находят расстояния ЕС и DC и вычисляют фокусное расстояние по формуле.
Прежде чем приступить к тщательному нахождению первого положения экрана (точка D), рекомендуется убедиться, получается ли при данном расположении приборов отчетливое действительное изображение объекта при одновременной работе обеих линз.
Способ 2. Определение фокусного расстояния при помощи зрительной трубы. Если точка D совпадает с фокусом рассеивающей линзы, то согласно формуле (5) точка Е должна переместиться в бесконечность, т.е. лучи после рассеивающей основан второй способ определения фокусного расстояния рассеивающей линзы.
Измерения. Найдя, как и прежде положение изображения, даваемого собирательной линзой (точку D), удаляют экран; помещают исследуемую линзу между найденным положением экрана и собирательной линзой, а за рассеивающей линзой ставят оптическую трубу, установленную предварительно на бесконечность. Перемещая рассеивающую линзу, добиваются того, чтобы в трубе получилось отчетливое изображение сетки.
Отсчитывают найденное положение линзы; затем сдвигают ее и снова устанавливают. Сделав не менее десяти отсчетов, берут из них среднее.
Расстояние между найденным положением экрана и этим положением линзы дает фокусное расстояние последней.
