Мощность ламп в каждой фазе и общую мощность цепи

КОНТРОЛЬНАЯ РАБОТА

 

 

Специальность: Комплексное использование и

охрана водных ресурсов

 

Дисциплина: Электртехника и электроника

 

Работа студентки: 3-его курса

Чулаковой Юлии

 

Шифр: 4267

 

Калуга 2010

Задача 1.

В цепь синусоидального тока напряжением U=100В и частотой f = 50Гц включена катушка с активным сопротивлением R и индуктивным сопротивлением X.

Определить:

1. Ток I_k катушки.

2. Коэффициент мощности cosφ катушки.

3. Мощности катушки: полную S_k, активную P_k и реактивную Q_k.

4. Емкость конденсатора, который необходимо подключить параллельно катушке для получения в цепи резонанса токов.

5. Ток I₀ полную мощность S при резонансе токов.

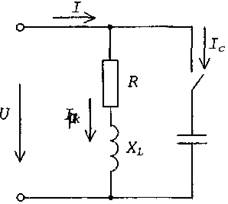6. Построить векторную диаграмму цепи до и после включения конденсатора.

 

Дано:

U = 100В

f = 50Гц

R = 7Ом

Х_L = 4Ом

Найти: I_k , cosφ_k, S_k, С₀, S.

Решение.

1. Ток в катушке определяем по закону Ома: ,

где - полное сопротивление катушки, Ом.

2. Коэффициент мощности катушки при известных сопротивлениях R и X_L определяем по формуле :

 

 

3. Полную мощность катушки вычисляем как S_k =U I_k:

S_{k = 100 ∙ 12,4 = 1210 BA}

Активную и реактивную мощности при известных сопротивлениях R и X_L определяем соответственно по формулам:

 

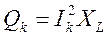
P_k=12,4²∙7=1076 Вт; Q_k=12,4²∙4=615 Вт.

 

4. Резонансную емкость С₀ найдем из условия резонанса токов (из равенства индуктивной и емкостной проводимостей параллельных ветвей):

где = 2π f - угловая частота; для частоты f =50 Гц ω=2π∙50=314 рад/с.

Вычисляем:

5. Входной ток цепи при резонансе токов I₀=GU,

где - активная проводимость данной цепи при резонансе. Таким образом,

Полная мощность цепи при резонансе S=UI₀=100∙10,78=1078 ВА,

при этом:

а) ток и полная мощность катушки сохраняют прежние значения, соответственно равные 12,4 А и 1210 ВА;

б) входной ток цепи равен активной составляющей тока катушки:

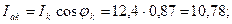
в) ток конденсатора

равен по величине реактивной составляющей тока катушки

и находится с ним в противофазе, т.е. сдвинут по фазе по отношению к реактивной составляющей тока катушки на 180°.

6. Для удобства построения векторной диаграммы выбираем разные масштабы для напряжения (m_U = 40В/ см) и для тока (m₁ = 2А/см). Вектор напряжения 0 в выбранном масштабе располагаем горизонтально.

Затем относительно вектора напряжения

строим векторы токов:

- совпадающий с вектором напряжения ;

- отстающий от напряжения на 90° (отложим от вектора напряжения по ходу часовой стрелки под углом 90°);

- опережающий напряжение на 90°

(отло­жим от вектора напряжения против хода часовой стрелки под углом 90°).

По активной и реактивной составляющим тока

ка­тушки строим ток , отстающий от на угол φ_k.

 

 

Задача 2.

В трехфазную сеть с линейным напряжением 380В по схеме «звезда с нулевым проводом» включены лампы накаливания мощностью Р_1л = 100Вт каждая. Сопротивлениями линейных проводов и нулевого провода пренебрегаем. Количество ламп n взять равным: в фазе А – n_А = 7шт., В – n_В = 4шт., С – n_С = 8шт.

Определить:

Мощность ламп в каждой фазе и общую мощность цепи.

Токи в фазах.

3. Построить в масштабе векторную диаграмму и из нее найти значение тока в нулевом проводе.

Дано:

U_Л= 380В;

n_А = 7шт.

n_В = 4шт.

n_С = 8шт.

Определить:

Р_А, Р_В, Р_С; I_А, I_В, I_С, I_N.

Решение.

 

1. Мощность ламп в каждой фазе определяем умножением мощно­сти одной лампы на число ламп в этой фазе:

Р_А = Р_л1∙ n_А = 100 ∙ 7 = 700Вт; Р_В = Р_л1∙ n_В = 100 ∙ 4 = 400Вт;

Р_С = Р_л1∙ n_С = 100 ∙8= 800Вт;

Общая мощность цепи равна сумме мощностей фаз:

Р = Р_А+ Р_В + Р_С = 700 + 400 + 800 = 1900Вт.

2. Ток в каждой фазе определяем из выражения Р_ф= U_ф∙I_ф∙ cosφ_ф,

где U_ф - напряжение на фазе потребителя (фазное напряжение);

I_ф - ток фазы, равный линейному току при соединении «звездой»;

cosφ_ф = 1, т.к. нагрузка имеет активный характер.

Так как U_А= U_В = U_С = U_ф =

3. Прежде чем строить век­торную диаграмму, выби­раем масштабы по напря­жению (m_U=50 B/см) и по току (m₁=1 А/см). Постро­ение диаграммы начинаем с построения векторов фаз­ных напряжений и , равных по величине, но сдвинутых относительно друг друга по фазе на 120˚. Векторы токов стро­им совпадающими с соот­ветствующими напряжени­ями, так как соs Φ = 1 и Φ = 0. Очевидно, что все токи не­обходимо строить в одном масштабе.

На основании I закона Кирхгофа ток в нулевом проводе равен геомет­рической сумме линейных токов:

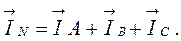
= 3,18+1,82+3,64 = 8,64A

Измерив длину вектора (в данном примере она равна 1,55 см).

Задача 3.

Вычертить схему и рассчитать основные электрические па­раметры однополупериодного выпрямителя с активным сопротивлением нагрузки R_н при питании от источника синусоидального напряжения U:

1. Среднее значение выпрямленного напряжения и тока U _{н ср} и I _{н ср}.

2.Среднюю мощность нагрузочного устройства Р_{н ср}.

3.Амплитуду основной гармоники выпрямленного напряжения U_{осн m}.

4.Коэффициент пульсаций р выпрямленного напряжения.