Последовательно включенные катушка индуктивности и конденсатор образуют колебательный контур, в котором возможен резонанс напряжения (см. на рис. 3.I.)Термин «резонанс напряжения» подразумевает, что при определенном условии, а именно, равенстве реактивных сопротивлений ХL=Хc, переменные напряжения на элементах контура L и C увеличиваются в Q раз по сравнению с напряжением подаваемым от источника на контур. Под величиной Q понимается добротность контура, равная Q =ХL/R. 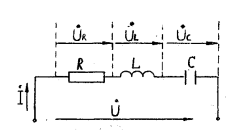
Рис.3.1.Эквивалентная электрическая схема при последовательном включении резистора, индуктивности и конденсатора.
На схеме обозначены элементы схемы R, L, C, векторы напряжения U и тока İ, протекающего через контур, а также векторы падения напряжений на элементах контура UR, Uс и UL.
Процессы, происходящие в исследуемой цепи (в соответствии со вторым законом Кирхгофа), описываются в случае постоянства величин R,L, C во времени и независимости их от величины протекающего тока, линейным интегрально-дифференциальным уравнением:
u(t)=R •i(t)+L• d[i(t)]/dt+1/C• ∫i(t) dt, (3.1)
где u(t) – переменное напряжение, подаваемое на колебательный контур,
R – величина сопротивления резистора,
L – величина индуктивности,
С – величина емкости,
i(t) –-переменный ток, протекающий в цепи.
В случае, когда поступающее на колебательный контур от генератора напряжение точно описывается синусоидальной функцией, а частота колебаний напряжения (f) постоянна, для решения уравнения можно использовать метод представления напряжений и токов в виде условных векторов на комплексной плоскости, вращающейся против часовой стрелки с частотой w.
Полное сопротивление для переменного тока электрической цепи, состоящей из последовательно включенных R-L-C –элементов при этом также целесообразно пре д ставлять в комплексном виде. Для того, чтобы отличить комплексные величины, их принято выделять подчеркиванием снизу. С учетом этого замечания выражение для полного сопротивления последовательно включенных элементов R-L-C записывается в следующем виде:
Z =| Z | • exp[jwt] =R+j X, (3.2)
где R – активное сопротивление цепи,
X = X L+ X c – полное комплексное реактивное сопротивление цепи,
X L=jwL=j| X L| – комплексное представление сопротивления индуктивности,
X c=1/jw C=-j| X c| – комплексное представление сопротивления емкости.
ХL=wL=2πfL – индуктивное сопротивление цепи для переменного напряжения,
X c=1/jwC – емкостное сопротивление цепи для переменного напряжения,

 Z=| Z | =√ R2 + (XL –Xc)2 - модуль полного комплексного сопротивления цепи, состоящей из последовательно включенных элементов R-L-C.
Z=| Z | =√ R2 + (XL –Xc)2 - модуль полного комплексного сопротивления цепи, состоящей из последовательно включенных элементов R-L-C.
Подставляя принятые обозначения в формулу (3.1.) можно записать выражение для напряжения, приложенного к рассматриваемой цепи в следующим виде:
u(t)= i(t) • | Z |= i(t)•  √R2 + (XL –Xc)2 (3.3)
√R2 + (XL –Xc)2 (3.3)
Таким образом решение интегрально –дифференциального уравнения (3.1.)
заменено решением простейшего алгебраического уравнения.
Параметры этого уравнения легко определяются из приведенных выше выражений.
Сдвиг фаз между током и напряжением определяется из выражения:
φ= arctg X/R, (3.4.)
где Х=XL–Xc – полное реактивное сопротивление цепи, равное алгебраической разности величин индуктивного и емкостного сопротивлений.
ПОСТРОЕНИЕ ВЕКТОРНЫХ ДИАГРАММ
Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:
- В цепи с активным сопротивлением ток и напряжение совпадают по фазе.
- В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов
- В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе напряжение на угол +90 градусов.
При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включении элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи.
Радиус-вектора на диаграммах выделяются жирным шрифтом или точками (черточками) над ними. При резонансе напряжений, когда ХL=Хс, полное сопротивление Z =R, то есть сопротивление контура оказывается чисто активным, а ток, протекающий через контур, достигает максимальной величины, равной
i(t)макс=u(t)/R (3.4)
В данном случае построение векторной диаграммы надо начинать с общего для цепи вектора тока İ, затем строятся векторы напряжений. При последовательном соединении катушки индуктивности и емкости общее реактивное сопротивление цепи X равно алгебраической разности индуктивного и емкостного сопротивлений X L и Хc. Приложенное к такой цепи напряжение можно представить в виде векторной суммы: вектора падения напряжения на активном сопротивлении (UR), совпадающего по фазе с вектором тока (İ), вектора падения напряжения на индуктивности (UL), опережающего ток по фазе на угол 90°, и вектора падения напряжения на емкости (Uc), отстающего от вектора тока на угол 90°.
При этом возможны следующие случаи:
а) Индуктивное сопротивление больше емкостного (X L >ХС). В этом случае входное напряжение будет опережать ток по фазе на угол φ.
б) Емкостное сопротивление больше индуктивного (X L <Хс). При этом ток опережает напряжение на угол φ.
в) Индуктивное сопротивление равно емкостному (XL =Xс). Соответственно полное реактивное сопротивление цепи (Х) равно нулю, а полное сопротивление цепи Z =R.При этом ток совпадает по фазе с напряжением (φ=0). Векторная диаграмма токов и напряжений для этого случая приведена на рис.3.2.

Рис.3.2.Векторная диаграмма для случая резонанса напряжений UL=Uc.
Явление резонанса напряжений широко используется в электронных схемах, в том числе в автогенераторах с кварцевыми резонаторами. Эквивалентная электрическая схема кварцевого резонатора обычно представляется в виде последовательно включенных R.L и C элементов.
СТРУКТУРНАЯ СХЕМА СТЕНДА.
Структурная схема модели стенда, используемого для изучения характеристик электрической цепи, состоящей из последовательно включенных катушки индуктивности и переменной емкости приведена на рис. 3.3.

Рис.3.3.Структурная схема модели стенда, используемого для изучения электрической цепи, состоящей из последовательно включенных катушки индуктивности и конденсатора.
На схеме слева направо обозначены: генератор электрического напряжения (U),вольтметр (V1) и амперметр (A1), измеряющие напряжение на контуре и ток протекающий от источника напряжения к контуру; ваттметр и фазометр с индикацией мощности, потребляемой контуром по показанию вольтметра V3, проградуированного в Ваттах на вольт (Active Power 1W/V) и вольтметра V4, проградуированного - 1 градус на милливольт (Phase Sift 1 grad/mv); вольтметра, измеряющего напряжение на катушке индуктивности (VRL); и вольтметра, измеряющего напряжение на емкости (Vc).
В изучаемой модели электрической цепи имеется возможность изменять величину емкости (С), индуктивности (L), резистора (R), а также величину напряжения, поступающего на контур от генератора напряжения электрической сети (U).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с описанием работы, моделью стенда и порядком проведения измерений.
2. Подготовить исходные материалы для составления отчета по работе. Для чего на отдельных листах бумаги заполнить титульный лист с фамилией, именем, отчеством студента, выполняющего лабораторную работу, Затем написать название дисциплины, название и цель выполнения лабораторной работы и выписать основные расчетные формулы.
3. Включить компьютер, запустить на выполнение программу «Eleсtronics Workbench» и открыть файл «Lab1.ewb», размещенный в папке «Электротехника и электроника», вложенной в папку «Лабораторные работы».
4. Вычертить электрическую схему исследуемой цепи с экрана монитора, обозначив на схеме вольтметры последовательно слева на правоV1, V2, V3, V4, V5, и амперметр А1.
5. Установить величину сопротивления равной R=1 Ом. Последовательно изменяя величины L и C провести 6 измерений по два раза для каждого из случаев: 1)XL>Xc; 2)ХL=Xc; 3)ХL<Xc; Для каждого случая последовательно записывать в табл. 3.1. показания вольтметров V1,V2,V3,V4,V5, и амперметра А1.Резонанс напряжений (ХL=Xc) удобно фиксировать по показаниям фазометра, равным φ=0.
Табл. 3.1.
| Измерено | Вычислено | ||||||||||||
| Величины | U (V1) | I1 (А1) | Р (V2) | φ (V3) | U RL (V4) | Uc (V5) | Zк | Z | R | XL | Xc | UL | UR |
| Ед. измер. | В | A | Вт | Градусы | В | В | Ом | Ом | Ом | Ом | Ом | В | В |
| XL>Xc | |||||||||||||
| XL>Xc | |||||||||||||
| XL>Xc | |||||||||||||
| XL=Xc | |||||||||||||
| ХL<Xc | |||||||||||||
| ХL<Xc | |||||||||||||
| ХL<Xc |
При расчете параметров колебательного контура можно использовать следующие формулы:
Полное сопротивление цепи,равно
 Z=| Z | =√R2 + (XL –Xc)2
Z=| Z | =√R2 + (XL –Xc)2
Емкостное сопротивление X c = Uc/I=1/ w C=1/2 π f C.
Индуктивное и активное сопротивление катушки Zк =Uк/I; R=P/I2
Индуктивное сопротивление катушки ХL=√Zк2- R2
Коэффициент мощности cos φк =P/UI.
Напряжения на индуктивности и резисторе UL=XLI; UR=I R
Добротность контура Q=ХL/R.
6.По результатам измерений и расчетов каждый студент должен построить векторную диаграмму для одного из режимов работы. Построение диаграммы начинается с вектора тока İ (см. рис 3.4.).Вектор напряжения на катушке индуктивности равен сумме векторов Uк=UR+UL.
Направление вектора падения напряжения на активном сопротивлении UR совпадает с направлением вектора тока İ. Вектор падения напряжения на индуктивности UR опережает вектор тока на 90 градусов. Построив в масштабе вектора UR и UL и сложив их получим вектор падения напряжения на катушке индуктивности Uк, который опережает вектор тока İ на угол φк. Сложив вектора Uк и Uс получим вектор напряжения U, который как видно из диаграммы на рис3.6. отстает от вектор тока İ на угол φ, то есть векторная диаграмма построена для случая, когда ХL меньше Хс.
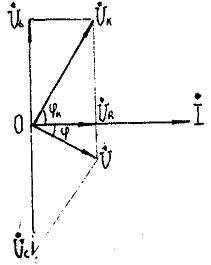
Рис.3.4. Векторная диаграмма для случая, когда Хс больше ХL.
7.Рассчитать значение добротности контура для случая резонанса, а также величины напряжений UL, и Uс на элементах контура при резонансе напряжений. Сравнить расчетные и измеренные значения напряжений UL, и Uс при резонансе напряжений.
3.5. СОСТАВЛЕНИЕ ОТЧЕТА ПО РАБОТЕ. Отчет должен содержать:
1. Титульный лист с названием университета, факультета, кафедры, курса, специальности, дисциплины, лабораторной работы, фамилии, имени, отчества студента.
2. Цель работы.
3. Схему модели лабораторного стенда, вычерченную с помощью линейки.
4. Таблицы, содержащие результаты измерений и расчетов.
5. Векторные диаграммы, графики зависимостей напряжений, токов и других величин, построенные по результатам измерений осциллограммы напряжений и токов. Векторные диаграммы должны строится с помощью линейки, с соблюдением масштабов (например, масштаб тока Мi, масштаб напряжения Мv), обозначением всех векторов и сдвига фаз между векторами.
6/Выводы.
ЛАБОРАТОРНАЯ РАБОТА №4.
ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ. РЕЗОНАНС ТОКОВ
Файл«Lab4. ewb» (res. i. ewb.)
4.1.ЦЕЛЬ РАБОТЫ. Изучение процессов в исследуемой цепи. Изучение явления резонансов токов. Изучение построения компенсаторов реактивной мощности.






