Целью работы является определение криоскопической постоянной воды по температуре начала кристаллизации разбавленных водных растворов некоторых нелетучих органических веществ (глюкоза, сахароза, мочевина и др.).
Выполнение работы требует предварительного изучения теории идеальных и разбавленных растворов, знания правила фаз Гиббса.
Теоретические сведения
Равновесная кристаллизация индивидуальных жидкостей происходит при строго фиксированной температуре (T 1), зависящей от внешнего давления. Принято называть нормальной температурой плавления (кристаллизации) вещества температуру при равновесии жидкой и твердой фаз под давлением в 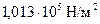 (I атм). По правилу фаз Гиббса число степеней свободы двухфазной однокомпонентной системы при фиксированном давлении равно нулю. Это означает, что в процессе обратимой кристаллизации температура остается постоянной до тех пор, пока в системе присутствует жидкая фаза.
(I атм). По правилу фаз Гиббса число степеней свободы двухфазной однокомпонентной системы при фиксированном давлении равно нулю. Это означает, что в процессе обратимой кристаллизации температура остается постоянной до тех пор, пока в системе присутствует жидкая фаза.
Растворы, как правило, кристаллизуются в некотором интервале температур. Температура, при которой из раствора выпадают первые кристаллы твердой фазы, называется температурой начала кристаллизации (Т). В случае, когда из раствора при постоянном давлении выпадают кристаллы чистого растворителя, из двух переменных (температура и концентрация растворителя в жидком растворе x 1) произвольно при 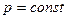 можно варьировать лишь одну, так как число степеней свободы системы равно единице:
можно варьировать лишь одну, так как число степеней свободы системы равно единице:

| (70) |
Для идеальных растворов температура начала кристаллизации Т связана с составом раствора уравнением:
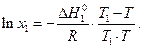
| (71) |
В этом соотношении 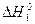 и T 1 – мольная теплота и температура плавления чистого растворителя соответственно.
и T 1 – мольная теплота и температура плавления чистого растворителя соответственно.
Разность между температурами плавления чистого растворителя и начала кристаллизации раствора называют понижением температуры кристаллизации. Согласно (1) эта величина
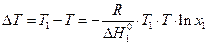
| (72) |
Уравнение (71) может быть применено к растворителю в бесконечно разбавленном растворе, поскольку по отношению к нему раствор является идеальным. Кроме того, это равенство может быть упрощено. Действительно, в разбавленном растворе мольная доля растворенного вещества «2» 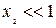 , поэтому
, поэтому
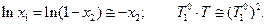
| (73) |
В разбавленных растворах химический состав удобнее характеризовать величиной моляльности m, т.е. числом молей растворенного вещества в 1000 г растворителя. Если раствор приготовлен из g 1 граммов растворителя с молярной массой М 1 и g 2 граммов растворенного вещества с молярной массой M 2, то число молей компонента 2, приходящихся на I грамм растворителя, составит 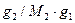 молей. Моляльность такого раствора определяется равенством:
молей. Моляльность такого раствора определяется равенством:

| (74) |
Выразим мольную долю компонента 2 через моляльность раствора. Так как в рассматриваемом растворе 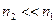 , то
, то
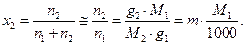
| (75) |
Таким образом, с учетом (73) и (75) уравнение (72) принимает вид:
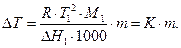
| (76) |
Величину
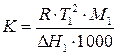
| (77) |
называют криоскопической постоянной растворителя, она зависит лишь от его природы и не зависит от концентрации и природы растворенного вещества. Согласно (76) понижение температуры кристаллизации разбавленного раствора прямо пропорционально числу растворенных частиц в 1000 г растворителя. Поэтому величина Δ T при заданной моляльности раствора будет зависеть и от степени диссоциации растворенного вещества.
Порядок выполнения работы
Понижение температуры кристаллизации раствора определяют с помощью установки, схема которой приведена на рис. 12.

Пробирку 1 с исследуемым раствором необходимо поместить в холодильник 2 и ввести в раствор «рабочий» конец термобатареи 3. Термобатарея представляет собой несколько последовательно включенных дифференциальных термопар (более 10 штук), которые многократно усиливают сигнал, получаемый от исследуемой системы. Другой конец термобатареи находится при комнатной температуре. В этом случае электрический сигнал с термобатареи характеризует температуру охлаждения раствора от времени. Типичный вид кривой охлаждения приведен на рис. 13.
Tемпературой начала кристаллизации раствора следует считать наивысшую температуру t нк (рис. 13), полученную после переохлаждения. Для ее точного определения следует внимательно следить за показаниями цифрового вольтметра 5. В области переохлаждения из раствора начинают выпадать кристаллы. Этот процесс сопровождается выделением тепла, а следовательно, повышением температуры до значения температуры начала кристаллизации (точка tнк на рис.13, кривая б). Таким образом, показания вольтметра сначала уменьшаются, (по абсолютному значению увеличиваются, так как измерение проходит в области температур пониженных относительно комнатной), затем увеличиваются до температуры начала кристаллизации, после чего снова уменьшаются – кривая б на рис. 13. Температуру кристаллизации растворителя определяют не менее трех раз. Для нагрева исследуемого раствора до исходной температуры используют стакан с горячей водой 4. Результаты измерений заносят в табл. 8.
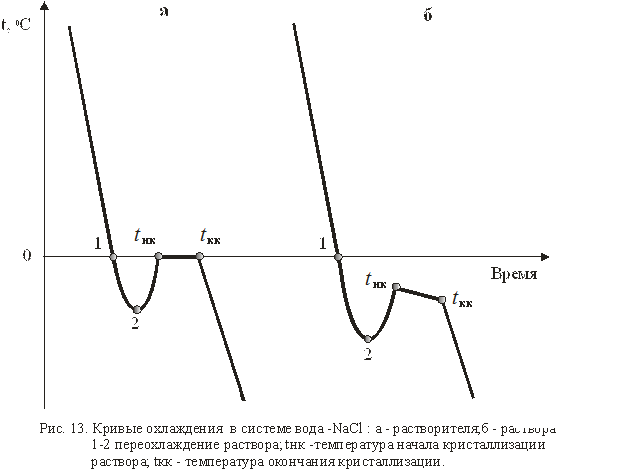
Таблица 8
Экспериментальные данные
| № опыта | Концентрация растворенного вещества, мас. % | Моляльная концентрация раствора (mi), моль/кг | Температура кристаллизации
растворителя 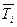 , K , K
| Понижение
температуры
кристаллизации
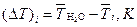
| |||
среднее
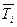
| |||||||
| … n |
Понижение температуры замерзания находят как разницу между температурой кристаллизации чистого растворителя (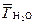 ) и температурой кристаллизации растворителя из раствора (
) и температурой кристаллизации растворителя из раствора (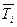 ).
).
По данным табл. 8 строят график зависимости понижения температуры кристаллизации растворителя от моляльной концентрации раствора. Угловой коэффициент полученной прямой определяет опытное значение криоскопической постоянной (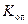 ). Его можно рассчитать по формуле
). Его можно рассчитать по формуле
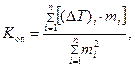
| (78) |
где 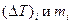 – значения понижения температуры кристаллизации растворителя и моляльность раствора в i -м опыте соответственно.
– значения понижения температуры кристаллизации растворителя и моляльность раствора в i -м опыте соответственно.
Данная формула получена методом наименьших квадратов из условия: сумма квадратов отклонений экспериментальных точек от прямой, проходящей через начало координат и имеющей угловой коэффициент, равный 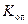 , должна быть минимальной. Для расчета
, должна быть минимальной. Для расчета 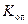 следует заполнить табл. 9.
следует заполнить табл. 9.
Таблица 9
К расчету опытного значения криоскопической постоянной
| № опыта | 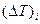 ,
K ,
K
| 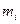 ,
моль/кг ,
моль/кг
| 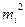 ,
моль2/кг2 ,
моль2/кг2
| 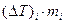 ,
моль×К/кг ,
моль×К/кг
| 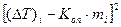 ,
К2 ,
К2
|
| … n |
Случайную погрешность величины 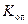 , найденной методом наименьших квадратов, рассчитывают по формуле
, найденной методом наименьших квадратов, рассчитывают по формуле
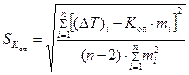
| (79) |
Опытное значение криоскопической постоянной сравнивают с рассчитанным по уравнению (78). Если разница между 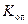 и
и 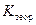 не превосходит
не превосходит 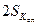 , то можно пренебречь систематической погрешностью. В противном случае следует оценить систематическую погрешность δ:
, то можно пренебречь систематической погрешностью. В противном случае следует оценить систематическую погрешность δ:
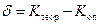
| (80) |
и по формуле (6), приведенной в третьей части «Руководства», определить суммарную погрешность 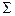 .
.
Затем требуется оценить целесообразное число значащих цифр в записи результатов измерений и представить результат с указанием погрешности.
Контрольные вопросы
1. Чему равно число степеней свободы при равновесии жидкого раствора с чистым твердым растворителем?
2. Чем определяется величина изменения температуры кристаллизации Δ Т?
3. Для каких растворов наблюдается линейная связь понижения температуры кристаллизации с моляльностью?
4. Каким образом природа растворенного вещества может повлиять на величину изменения температуры кристаллизации?
5. Как измерить температуру кристаллизации в данной работе?
6. От каких факторов зависит криоскопическая постоянная; от каких факторов криоскопическая постоянная не зависит?
ПРИЛОЖЕНИЕ 1. Термодинамические свойства некоторых веществ
| Вещество | 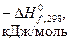
| 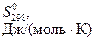
| 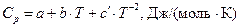
| ||
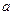
| 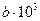
| 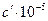
| |||
| СО2 газ | 393,51 | 213,66 | 44,14 | 9.04 | -8,79 |
| СО газ | 110,53 | 197,55 | 28,41 | 4,10 | -0,46 |
| С граф | 5,74 | 16,86 | 4,77 | -8,54 | |
| СаО тв | 635,09 | 38,07 | 49,62 | 4,52 | -6,95 |
| СаСО3 тв | 1206,83 | 91,71 | 104,52 | 21,92 | -25,94 |
ПРИЛОЖЕНИЕ 2. Расчет величины 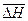 в работах №1 и №2
в работах №1 и №2
Среднюю величину теплового эффекта реакции в изученном интервале температур (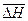 ) можно оценить по опытным значениям константы равновесия при разных температурах. Для этого необходимо проинтегрировать уравнение изобары химической реакции, считая
) можно оценить по опытным значениям константы равновесия при разных температурах. Для этого необходимо проинтегрировать уравнение изобары химической реакции, считая 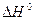 постоянным:
постоянным:
 ,
,
после интегрирования получим
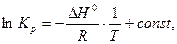
где 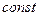 – постоянная интегрирования. Из данного соотношения следует, что опытные данные, представленные в координатах «
– постоянная интегрирования. Из данного соотношения следует, что опытные данные, представленные в координатах «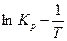 », должны располагаться около прямой линии, угловой коэффициент которой
», должны располагаться около прямой линии, угловой коэффициент которой 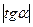 равен
равен 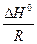 .
.
Следовательно, 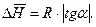
При нахождении углового коэффициента необходимо учесть, что масштаб оси абсцисс и оси ординат различен. Поэтому 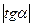 следует находить как отношение катетов прямоугольного треугольника, длины которых выражены в единицах соответствующих осей.
следует находить как отношение катетов прямоугольного треугольника, длины которых выражены в единицах соответствующих осей.
Таким образом,
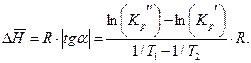
ПРИЛОЖЕНИЕ 3. Интегральные теплоты растворения некоторых солей в воде при 25ºС
| Соль | KI | NH4Cl | KCl | NaCl |
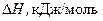
| 20,59 | 15,23 | 17,55 | 4,25 |
Библиографический список
1. Жуховицкий А.А. Физическая химия / А.А. Жуховицкий, Л.А, Шварцман. М.: Металлургия, 2001. 688с.
2. Стромберг А.Г. Физическая химия / А.Г. Стромберг, Д.П. Семченко. М.: Высшая школа, 1988. 496 с.
3. Карапетьянц М.Х. Химическая термодинамика / М.Х. Карапетьянц, М.: Химия, 1985. 580 с.
4. Краткий справочник физико-химических величин/ Под ред. А.А. Равделя и А.М. Пономаревой. СПб: Медный всадник, 2003. 240 с.
5. Зайдель А.Н. Погрешности измерений физических величин. Л.: Наука, 1985. 112 с.






