ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
 |
Московский государственный университет
Приборостроения и информатики
Кафедра высшей математики
Выборнов А.Н.
ПОСОБИЕ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНАЦИОННОМУ ТЕСТИРОВАНИЮ ПО МАТЕМАТИКЕ ЗА 1 СЕМЕСТР
Москва 2002
Рассмотрим решения основных типов задач экзаменационного теста:
1. Решить матричное уравнение 
Решение: 
Найдем 
. Вычислим определитель матрицы 
.
Далее 
.
Ответ: 
.
Вычислить определитель.
Решение: Используя свойства определителей, вычтем из 3-й строки определителя 1-ю и 2-ю строки, определитель при таких преобразованиях не меняется.
Получим:
.
Разложим теперьопределитель по 3-й строке:
.
Ответ: 
.
3. Сколько решений имеет система 
Решение: В этой системе уравнений меньше чем неизвестных, поэтому возможна только одна из двух ситуаций: система не имеет решений или система имеет бесконечное множество решений. Для того чтобы выяснить, какая из ситуаций имеет место в данном случае, приведём расширенную матрицу системы к ступенчатому виду (используем метод Гаусса решения систем).
.
Мы видим, что в получившейся ступенчатой расширенной матрице есть длинная ступенька (подчёркнута два раза). Следовательно, система имеет бесконечное множество решений.
Ответ: бесконечное множество решений.
Решить систему (x, y - неизвестные).
Решение: Используем метод Крамера:
Ответ: 
.
Решение: векторы параллельны тогда и только тогда, когда их координаты пропорциональны: 
.
Ответ: 
.
6. Найти сумму координат векторного произведения 
Решение:
,
.
Ответ: 
.
При каком значении m точки A, B, C, D лежат в одной плоскости?
A(m; 1; 2), B(3;-1; 4), C(2; 1; 3), D(5; 1; 4).
Решение:
Точки A(m; 1; 2), B(3;-1; 4), C(2; 1; 3), D(5; 1; 4)лежат в одной плоскости тогда и только тогда, когда векторы 
компланарны.
компланарны тогда и только тогда, когда смешанное произведение
. Смешанное произведение 
- это определитель, у которого по строкам записаны координаты векторов :
. Разложим этот определитель по второму столбцу:
Ответ: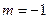 
.
Найти уравнение прямой, проходящей через точку А(2; -1) перпендикулярно прямой.
Решение:
 |
Нормальный вектор
к прямой 
будет параллелен искомой прямой, то есть может служить направляющим вектором этой прямой. Поэтому используем каноническое уравнение:
Ответ: 
.
Решение: Используем условие параллельности прямых, заданных своими общими уравнениями: 
В нашем случае:
Ответ: 
.
Решение: Вторая прямая задана параметрическими уравнениями. Найдём при каком значении параметра 
точка второй прямой попадает на первую прямую. Для этого выражения для 
и 
из второго уравнения подставим в первое уравнение:
Теперь найдём координаты точки пересечения прямых:
Ответ: 
.
Решение: 
Из уравнения плоскости 
получим координаты нормального вектора
. Этот нормальный вектор, перпендикулярный плоскости будет перпендикулярен и искомой плоскости. Запишем теперь уравнение искомой плоскости (нам известны координаты точки на плоскости и координаты нормального вектора):
Ответ: 
.
Решение:
Вектор 
будет параллельным искомой прямой.
Запишем теперь каноническое уравнение искомой прямой (известны координаты точки А на этой прямой и координаты направляющего вектора 
):
Ответ: 
.
Решение: Эти три плоскости имеют ровно одну общую точку тогда и только тогда, когда система линейных уравнений
имеет ровно одно решение. Это будет выполнено тогда и только тогда, когда определитель матрицы системы будет не равен нулю. Итак:
Ответ: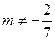 
.
Решение: Переведём канонические уравнения прямой в параметрические уравнения:
Подставим выражения для 
из параметрических уравнений прямой в уравнение плоскости и найдём при каком значении прямая пересекает плоскость:
Найдём теперь координаты точки пересечения прямой и плоскости, для этого найденное значение подставим в параметрические уравнения прямой:
Ответ: 
.
Решение: Найдём точки пересечения плоскости и координатных осей:
С осью 
: подставим в уравнение плоскости 
. Получим: 
.
Итак, точка 
- точка пересечения с осью . Аналогично получим точку 
- точку пересечения с осью 
, и точку 
- точку пересечения с осью 
. 
В пирамиде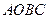 
в основании лежит 
, причём это прямоугольный треугольник с катетами 
и 
.
Найдём площадь основания: 
.
Отрезок 
является высотой в пирамиде .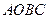
Найдём объём пирамиды: 
.
Ответ: 
.
Решение:
Найдём координаты нормального вектора к плоскости 
:
.
Найдём координаты направляющего вектора прямой 
:
.
Плоскость и прямая будут параллельны тогда и только тогда, когда векторы 
и 
будут перпендикулярны. Далее
Ответ: 
.
Решение:
Найдём любую точку на прямой 
, для этого положим 
в параметрических уравнениях этой прямой: 
. Получили точку 
.
Найдём расстояние от этой точки до плоскости 
, используя формулу:
Итак: 
Ответ: 
.
Решение: В уравнении коэффициенты при 
и при 
, а также свободный член в правой части уравнения положительны. Уравнение можно привести к виду:
. Это уравнение эллипса.
Ответ: эллипс.
Решение: В уравнении присутствует переменная 
в первой степени, а переменные и во второй степени. Значит это уравнение параболоида. Кроме того, знаки коэффициентов при и при совпадают – значит это эллиптический параболоид.
Ответ: параболоид эллиптический.
Решение:
1способ. Матрица перехода от базиса 
к базису 
имеет вид:
.
Координаты вектора 
в старом и новом базисах связаны соотношением: 
.
Отсюда получим: 
. Найдём 
.
Найдём теперь новые координаты вектора :
.
2способ.
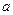Обозначим неизвестные координаты вектора в новом базисе буквами 
и 
.
Тогда имеет место равенство:
Получим систему двух линейных уравнений с неизвестным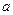и и :
.
Решив систему, получим 
.
Ответ: 
