В 1963 году американский ученый Д. Ганн обнаружил, что кристалл арсенида галлия с электронной электропроводностью под действием сильного электрического поля способен генерировать СВЧ-колебания. Это явление получило название эффекта Ганна, а созданные на его основе приборы — диодов Ганна. Строго говоря, эти приборы не являются диодами, поскольку в них отсутствует выпрямляющий электронно-дырочный переход. В зарубежной литературе чаще используется сокращенное название TED (Transferred Electron Devices). Приборы на основе эффекта Ганна правильнее отнести к приборам функциональной электроники, так как в них преобразование энергии постоянного тока в энергию СВЧ-колебаний происходит за счет сложных физических процессов в кристалле арсенида галлия. Чтобы понять эти процессы, необходимо внести некоторые уточнения в зонную модель полупроводника, которой мы до сих пор пользовались для объяснения процессов в полупроводниковых диодах и транзисторах. Известно, что энергия свободного электрона равна
,
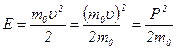где Р = mo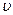 
— импульс электрона.
Согласно формуле Луи де Бройля,
,
где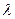 
— длина электронной волны;
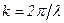— волновой вектор электрона, по направлению совпадающий с направлением распространения электронной волны.
Следовательно, энергию свободного электрона можно выразить через волновой вектор k:
.
Отсюда следует, что зависимость энергии свободного электрона от его волнового вектора имеет квадратичный характер.
В твердом теле на электрон действует периодическое потенциальное поле кристаллической решетки. Чтобы описать сложные законы движения электрона в кристалле с помощью соотношений классической механики, влияние внутренних сил на электрон учитывают, заменив массу свободного электрона m0 эффективной массой т*. Импульс Р=m*v называется квазиимпульсом электрона. Тогда диаграмму энергетических зон полупроводника в k- пространстве можно представить так, как это показано на рис. 9.11, а.
При упрощенном рассмотрении энергетической диаграммы вместо истинных кривых, ограничивающих валентную зону и зону проводимости, проводят две параллельные прямые: одну — касательную к дну зоны проводимости, вторую — касательную к вершине валентной зоны. Первую прямую принимают за нижнюю границу зоны проводимости Ес , вторую — за верхнюю границу валентной зоны Ev. Расстояние между ними равно ширине запрещенной зоны 
.
Зона проводимости полупроводника может быть образована из нескольких перекрывающихся между собой разрешенных энергетических зон. В этом случае энергетическая диаграмма зоны проводимости в k- пространстве может иметь минимум, смещенный относительно точки k = 0 (рис. 9.11, б), что имеет место в кремнии. В кристалле арсенида галлия имеются два минимума (рис, 9.11, в) в кристаллографическом направлении (100), которые называются энергетическими долинами. Полупроводник в этом случае называется двухдолинным. Минимальная энергия электронов, имеющая место при k = 0, соответствует нижней границе зоны проводимости. Верхняя долина отделена от нижней долины энергетическим зазором 
= 0,36 эВ.
Эффективные массы электронов, находящихся в нижней и верхней долинах, различаются по значению. В нижней долине 
, в верхней —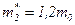 
. Подвижность электронов равна
,
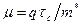где 
— среднее время между столкновениями с решеткой. Подвижность электронов различна для нижней и верхней долин: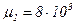 
см/В*с, 
см/В*с. Следовательно, скорость дрейфа «легких» электронов нижней долины, пропорциональная напряженности внешнего поля 
, почти на два порядка больше скорости дрейфа «тяжелых» электронов верхней долины.
При комнатной температуре практически все электроны проводимости находятся в нижней долине. При увеличении температуры все большее число электронов приобретает энергию, достаточную для перехода в верхнюю долину. В результате нижняя долина опустошается, а верхняя — заполняется. Этот процесс называется междолинным переходом.
Увеличение энергии электронов можно осуществить не только повышением температуры кристалла, но и с помощью внешнего электрического поля, изменяя напряженность которого, можно управлять междолинным переходом электронов. Величина напряженности поля, при которой начинается интенсивный междолинный переход, называется пороговой и обозначается 
. Для арсенида галлия она равна примерно 3,2 кВ/см.
Найдем плотность дрейфового тока, протекающего через идеальный кристалл n- типа, в котором обеспечена абсолютная однородность электрического поля, создаваемого в нем приложенным к контактам внешним напряжением. Учтем, что ток создается как «легкими», так и «тяжелыми» электронами, суммарная концентрация которых, равная 
, не зависит от напряженности поля, так как определяется только концентрацией доноров. Следовательно, плотность тока равна
.
Умножив и разделив правую часть на n0, получим
.
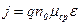Здесь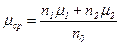 
— усредненная по двум долинам подвижность.
Учитывая, что дрейфовая скорость электронов равна 
получим
То есть плотность дрейфового тока пропорциональна скорости дрейфа 
.
В слабых полях 
. По мере роста начиная с некоторойвеличины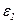 
электроны переходят из нижней долины в верхнюю, поэтому n1 уменьшается, п2 увеличивается (рис. 9.12, a), 
уменьшается (рис. 9.12, б), а рост замедляется (рис. 9.12, в).
Начиная с величины , интенсивность междолинных переходов возрастает настолько, что резко уменьшается, вследствие чего уменьшается . При 
междолинные переходы завершаются, нижняя долина оказывается почти полностью опустошенной (n1 = 0), а верхняя — заполненной (п2 = n0). При этих условиях
.
Если = 8 кВ/см, то наступает насыщение дрейфовой скорости, поэтому при 
скорость остается постоянной.
Принимая во внимание, что плотность тока пропорциональна , величина тока связана с плотностью тока соотношением i=jS, где S — площадь поперечного сечения кристалла, а напряженность поля = u/L, где и — напряжение, приложенное к кристаллу, L — длина кристалла, можно записать уравнение вольт-амперной характеристики кристалла:
.
Из этого уравнения следует, что зависимость тока от напряжения аналогична зависимости дрейфовой скорости от напряженности поля, то есть она содержит участок с отрицательным дифференциальным сопротивлением (рис. 9.13). Существование отрицательного дифференциального сопротивления обусловлено уменьшением дрейфовой скорости при увеличении напряженности поля. При напряжении и, соответствующем критической напряженности поля, равной примерно 8 кВ/см, дрейфовая скорость становится постоянной и рост тока прекращается.
Наличие отрицательного дифференциального сопротивления может компенсировать потери в присоединенной к кристаллу пассивной цепи, что позволяет использовать его для генерации и усиления электрических колебаний. Это обстоятельство нашло применение в СВЧ-устройствах, работающих на частотах, измеряемых единицами и десятками гигагерц. Рассмотрим принцип генерирования СВЧ-колебаний, основанный на использовании эффекта Ганна.
В кристалле арсенида галлия имеются неоднородности, обусловленные неравномерностью распределения легирующей примеси и дефектами кристаллической структуры, в результате чего в нем возникают локальные напряженности поля, превышающие среднюю напряженность. Как правило, эти неоднородности существуют вблизи торцов кристалла, на которые напылены внешние металлические электроды катода и анода (рис. 9.14, а). Основную роль играют неоднородности у катодного вывода. Пусть в момент включения внешнего напряжения в кристалле возникает электрическое поле со средней напряженностью поля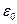 
, которая несколько меньше пороговой напряженности . Из-за наличия неоднородностей напряженность поля в околокатодной области оказывается выше пороговой (рис. 9.14, б). Вследствие этого левее сечения x1 , появляются «тяжелые» электроны, движущиеся со скоростью 
а правее х1 находятся «легкие» электроны, движущиеся со скоростью 
. По мере продвижения «тяжелых» и «легких» электронов к аноду формируется зарядовый пакет, называемый доменом. Он состоит из двух слоев (рис. 9.14, б): слой со стороны катода из-за избытка «тяжелых» электронов имеет отрицательный заряд, слой со стороны анода из-за недостатка «легких» электронов имеет положительный заряд. Наличие этих зарядов ведет к образованию электрического поля домена, направленного в ту же сторону, что и внешнее поле (рис. 9.14, г). По мере формирования домена поле в нем растет, а за пределами домена - уменьшается. Поэтому скорость движения «тяжелых» электронов внутри домена возрастает, а скорость движения «легких» электронов за пределами домена уменьшается. В некоторый момент времени t1, скорости движения «легких» и «тяжелых» электронов становятся одинаковыми, и формирование домена завершается. Сформированный домен продолжает двигаться к аноду со скоростью 
.Достигнув анода, домен рассасывается, в структуре устанавливается исходное распределение напряженности поля (рис. 9.14, б) и начинается формирование нового домена. Зная закономерности изменения скоростей «тяжелых» и «легких» электронов, нетрудно объяснить характер изменения тока во внешней цепи. В момент включения t0 в кристалле все электроны являются «легкими», и плотность тока через кристалл имеет максимальное значение:
.
По мере формирования домена возрастает напряженность поля внутри домена и уменьшается вне его пределов, при этом снижается дрейфовая скорость и, соответственно, ток. После образования домена (момент t1) в кристалле установится минимальный ток
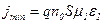
В момент t2 домен достигает анода и рассасывается в интервале 
при этом ток возрастает. Изменение тока во времени иллюстрирует рис. 9.15. Частота следования импульсов определяется дрейфовой скоростью домена и длиной кристалла L:
При L =10 мкм и = 107 см/с частота колебаний составляет 10 ГГц.
На основе эффекта Ганна выполняют также СВЧ-усилители, рабочая точка которых находится на падающем участке вольт-амперной характеристики. Усиление мощности такого усилителя на частоте 25-30 ГГц достигает 60-70. На основе эффекта Ганна могут также выполняться элементы логических схем, быстродействие которых достигает 10-10-10-11 с. Кроме того, на основе эффекта Ганна выполняют импульсные усилители, работающие в триггерном режиме. На основе эффекта Ганна могут быть созданы элементы памяти, аналого-цифровые преобразователи и ряд других устройств.
Контрольные вопросы
1. Какие существуют проблемы повышения степени интеграции?
2. В чем состоят основные особенности больших интегральных схем?
3. Что такое акустоэлектронные устройства и как они работают?
4. Что такое магнитоэлектронные устройства и как они работают?
5. Что такое оптоэлектронные устройства и как они работают?
6. В чем состоит сущность эффекта Ганна?
