I семестр
Множества и функции
Операции над множествами (объединение, пересечение, разность, дополнение). Множества натуральных, целых, рациональных чисел, их изображение на числовой прямой. Принцип математической индукции. Неравенство Бернулли, формула бинома Ньютона.
Действительное число как бесконечная десятичная дробь. Взаимно однозначное соответствие между точками прямой и действительными числами. Порядок на множестве R действительных чисел. Ограниченные числовые множества, определения верхней и нижней грани. Теорема о существовании верхней грани ограниченного сверху числового множества, нижней грани ограниченного снизу числового множества. Определение операций на множестве R. Свойства операций (без доказательств).
Функции. Способы их задания. График функции. Композиция функций. Обратимые функции, график обратной функции. Простейшие преобразования графиков функций.
Высказывания, операции над высказываниями. Таблицы истинности логических связок. Тавтологии, правила логического вывода. Предикаты; кванторы.
Предел и непрерывность
Определение последовательности. Предел последовательности. Примеры сходящихся последовательностей, примеры расходящихся последовательностей. Основные теоремы о пределах последовательностей (единственность предела, ограниченность сходящейся последовательности, переход к пределу в неравенстве, теорема о зажимающих последовательностях).
Леммы о бесконечно малых последовательностях. Теоремы об арифметике пределов. Ограниченные последовательности. Теорема о сходимости монотонной ограниченной последовательности. Теорема о выборе сходящейся подпоследовательности из ограниченной последовательности.
Критерий Коши сходимости последовательности.
Вычисление пределов последовательностей (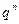 ),
),  , (
, ( ), (
), (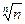 ).
).
Число e. Предел последовательности  при
при  , где
, где 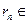 Q. Определение степени с действительным показателем. Показательная (экспоненциальная) функция, ее основные свойства.
Q. Определение степени с действительным показателем. Показательная (экспоненциальная) функция, ее основные свойства.
Два определения предела функции в точке и их эквивалентность. Теорема о единственности предела функции в точке, знакопостоянство функции, имеющей ненулевой предел. Предел слева, предел справа и их равенство. Бесконечно большие функции. Пределы функций при  ,
,  +
+ 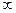 ,
,  -
- 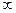 .
.
Теоремы о переходе к пределу в неравенстве. Арифметика пределов функций. Замечательный тригонометрический предел  при
при  .
.
Непрерывные функции. Простейшие свойства непрерывных функций. Непрерывность многочленов, дробно-рациональных функций, тригонометрических функций. Непрерывность функции, обратной к непрерывной.
Теорема о существовании и единственности логарифма. Логарифмическая функция, ее основные свойства. Непрерывность показательной и логарифмической функций. Нахождение пределов  ,
,  ,
,  ,
, 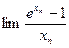 при
при  ,
,  ,
, 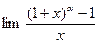 при
при  . Теоремы о промежуточном значении непрерывной функции. Теоремы об ограниченности непрерывной на отрезке функции, о достижении непрерывной на отрезке функцией наименьшего и наибольшего значений.
. Теоремы о промежуточном значении непрерывной функции. Теоремы об ограниченности непрерывной на отрезке функции, о достижении непрерывной на отрезке функцией наименьшего и наибольшего значений.
Дифференцируемость
Касательная к кривой как наиболее тесно прилегающая к ней прямая. Производное число функции в точке. Уравнение касательной к графику функции.
Теорема о линейном приближении. Непрерывность дифференцируемой функции. Пример функции, непрерывной в точке, но не дифференцируемой в ней.
Примеры вычисления производных: линейная функция, квадратичная функция, степенная функция 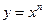 ,
, 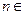 N, синус и косинус, логарифмическая функция
N, синус и косинус, логарифмическая функция  , показательная функция
, показательная функция  , арктангенс.
, арктангенс.
Арифметика производных: производные суммы, произведения, частного. Производная композиции функций (цепное правило). Примеры вычисления производных, использующие цепное правило: производные функций 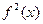 ,
, 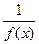 ,
,  ,
,  ,
, 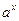 . Теорема о производной обратной функции. Вычисление производных обратных тригонометрических функций.
. Теорема о производной обратной функции. Вычисление производных обратных тригонометрических функций.
Определение дифференциала, его свойства. Производные и дифференциалы высших порядков.
Применение производной к исследованию функций
Теоремы Ферма, Ролля, Лагранжа. Возрастание и убывание функций. Понятие экстремума, необходимое условие экстремума. Наибольшее и наименьшее значения функций.
Выпуклость вверх, вниз; точки перегиба. Достаточные условия выпуклости. Достаточные условия экстремума.
Асимптоты функций. Общая схема исследования функции и построения ее графика..
Теорема Коши, обобщенная теорема Коши. Правило Лопиталя раскрытия неопределенностей.
Формула Тейлора. Разложение по степеням x функций  ,
,  ,
,  ,
, 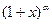 ,
,  . Некоторые применения формулы Лагранжа о среднем и формулы Тейлора.
. Некоторые применения формулы Лагранжа о среднем и формулы Тейлора.
5. Неопределенный интеграл
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов. Теорема о замене переменной. Примеры использования формулы замены переменной. Вторая теорема о замене переменной (подстановка). Вычисление интегралов  ,
, 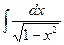 ,
,  ,
,  . Теорема об интегрировании по частям. Примеры использования формулы интегрирования по частям. Вычисление интегралов
. Теорема об интегрировании по частям. Примеры использования формулы интегрирования по частям. Вычисление интегралов  ,
, 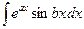 ,
,  . Обобщенная формула интегрирования по частям.
. Обобщенная формула интегрирования по частям.
Полярная запись векторов плоскости. Определение умножения векторов в полярной записи, координатная запись произведения. Свойства умножения. Поле комплексных чисел. Изоморфное вложение поля действительных чисел в поле комплексных чисел. Операция комплексного сопряжения. Правило деления комплексных чисел. Формула корней n -й степени из комплексного числа. Корни n -й степени из 1 и их расположение на плоскости.
Многочлены, сложение и умножение многочленов. Теорема о делении многочленов с остатком. Корни многочленов. Теорема Безу и следствия из нее. Кратные корни. Формулировка основной теоремы алгебры; следствия из нее. Теорема Виета. Теорема о корнях многочленов с действительными коэффициентами.
Разложение дробно-рациональной функции на сумму правильных дробей. Теорема о разложении дробно-рациональной функции на сумму простейших дробей над полем C. Формулировка теоремы о разложении дробно-рациональной функции на сумму простейших дробей над полем R.
Интегрирование простейших рациональных дробей − нахождение интегралов 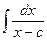 ,
,  ,
, 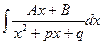 ,
,  , где
, где 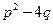 <0,
<0, 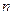 >1.
>1.






