№1
1а) Вычислить неопределенный интеграл: 
Данный интеграл вычислим при помощи формулы интегрирования по частям.
Выберем  ,
, 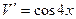 необходимо вычислить
необходимо вычислить  и
и 
(Определенную сложность для студентов зачастую представляет вычисление функции  при известном
при известном 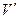 . Данную проблему можно решать следующими способами:
. Данную проблему можно решать следующими способами:
Первый подход рассчитан на студентов хорошо освоивших ранее пройденный материал и способных к интуитивному пониманию
1. Зная 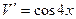 и представляя перед собой таблицу производных, понимаем, что данная производная может быть получена при дифференцировании функции
и представляя перед собой таблицу производных, понимаем, что данная производная может быть получена при дифференцировании функции  , причем именно
, причем именно  , однако
, однако  , значит для того чтобы производная получилась
, значит для того чтобы производная получилась  необходимо взять производную от функции
необходимо взять производную от функции  получения
получения
В случае если проведенные рассуждения сложны для восприятия, то возможен другой подход для вычисления искомой функции:
2. Учитывая второе основное свойство неопределенного интеграла  имеем
имеем


Либо интеграл  можно вычислить и другим способом:
можно вычислить и другим способом:
 таким образом, получаем
таким образом, получаем  .
.
Для вычисления  в итоге имеем:
в итоге имеем:



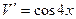
Применяем к исходному интегралу формулу интегрирования по частям  подставляя вместо
подставляя вместо  ,
, 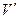 ,
,  и
и  их значения и получим:
их значения и получим:


1б) Вычислить неопределенный интеграл: 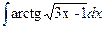
Для вычисления имеющегося интеграла целесообразно сначала сделать замену:
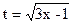

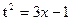





 имеем:
имеем:



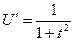



2) Вычислить определенный интеграл: 
Для вычисления имеющегося интеграла необходимо сначала вычислить соответствующий ему неопределенный интеграл  , а затем применить формулу Ньютона-Лейбница.
, а затем применить формулу Ньютона-Лейбница.
Данный неопределенный интеграл вычисляется при помощи формулы интегрирования по частям, причем применять ее придется два раза.







Применим к исходному интегралу формулу Ньютона-Лейбница.
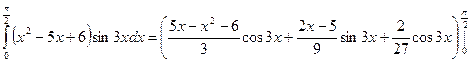


3) Найти неопределенный интеграл: 
Данный пример предполагает применение метода вычисления интегралов от дробно-рациональных функций.
Алгоритм наших действий следующий:
1. Выделяем целую часть, и получаем интеграл от многочлена и правильной дробно-рациональной функции.  т.е.
т.е. 
2. Представляем правильную дробно-рациональную функцию как сумму простейших дробей.  в силу единственности представления многочлена получаем систему уравнений:
в силу единственности представления многочлена получаем систему уравнений:
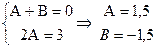 т.е.
т.е. 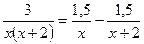
3. Вычисляем интегралы от простейших дробей.
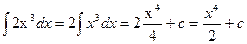



4. Записываем ответ как сумму от получившихся в третьем пункте выражений.

4a) Вычислить определенный интеграл: 
Перед нами определенный интеграл от тригонометрической функции. Сначала вычислим соответствующий ему неопределенный интеграл 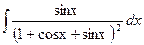 . Вычислять данный интеграл будем при помощи стандартной замены
. Вычислять данный интеграл будем при помощи стандартной замены  , при которой
, при которой  ,
,  ,
, 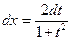 получим:
получим:

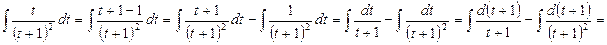

Теперь к исходному интегралу применяем формулу Ньютона-Лейбница.
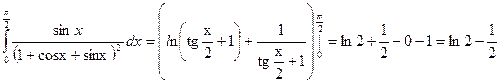
4б) Вычислить определенный интеграл: 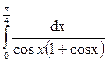
Перед нами определенный интеграл от тригонометрической функции. Сначала вычислим соответствующий ему неопределенный интеграл 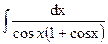 . Вычислять данный интеграл будем при помощи стандартной замены
. Вычислять данный интеграл будем при помощи стандартной замены  , при которой
, при которой  ,
,  ,
, 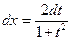 получим:
получим:

Перед нами интеграл от дробно-рациональной функции и вычислять его надо аналогично ранее решенному третьему примеру.
 ,
,  тогда имеем систему уравнений
тогда имеем систему уравнений 

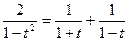
 Тогда
Тогда 
Применяя к исходному интегралу формулу Ньютона-Лейбница имеем:

5) Вычислить определенный интеграл: 
Перед нами определенный интеграл от иррациональной функции. Сначала вычислим соответствующий ему неопределенный интеграл  . Вычислять данный интеграл будем при помощи стандартной замены.
. Вычислять данный интеграл будем при помощи стандартной замены.
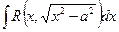
 замена
замена 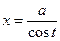 . В нашем случае замена
. В нашем случае замена  , при этом
, при этом 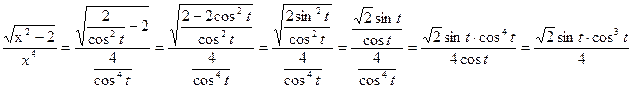 ,
,  , учтем что
, учтем что  в итоге имеем:
в итоге имеем:
 перед нами интеграл от тригонометрической функции, причем вида
перед нами интеграл от тригонометрической функции, причем вида  где m и n целые числа и одно из них не четное, можно занести
где m и n целые числа и одно из них не четное, можно занести  под знак дифференциала.
под знак дифференциала.
 проведя обратную замену и перейдя к исходной переменной имеем:
проведя обратную замену и перейдя к исходной переменной имеем: 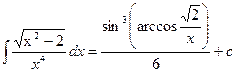 . Применяя к исходному интегралу формулу Ньютона-Лейбница имеем:
. Применяя к исходному интегралу формулу Ньютона-Лейбница имеем:

6) Вычислить длину дуги кривой, заданной в прямоугольной системе координат.  ,
, 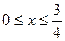
Если гладкая кривая задана уравнением  то длина ее дуги на отрезке [ a,b ] может быть вычислена по формуле:
то длина ее дуги на отрезке [ a,b ] может быть вычислена по формуле:  . В нашем случае
. В нашем случае 

 . Имеем:
. Имеем:
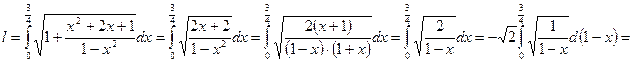

7) Изменить порядок интегрирования: 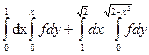
Для изменение порядка интегрирования первым шагом необходимо изобразить область, по которой вычисляется двойной интеграл.
В первой части исследуемого интеграла  внешняя переменная x изменяется от нуля до единицы образуя некую полосу на плоскости Oxy, а внутренняя переменная y изменяется от функции
внешняя переменная x изменяется от нуля до единицы образуя некую полосу на плоскости Oxy, а внутренняя переменная y изменяется от функции 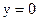 (горизонтальная прямая совпадающая с осью Ox) до функции
(горизонтальная прямая совпадающая с осью Ox) до функции  (прямая, которая является биссектрисой первого координатного угла). Обе функции могут быть построены по точкам.
(прямая, которая является биссектрисой первого координатного угла). Обе функции могут быть построены по точкам.

Таким образом получаем область:

Во второй части исследуемого интеграла 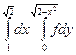 внешняя переменная x изменяется от единицы до
внешняя переменная x изменяется от единицы до  , образуя некую полосу на плоскости Oxy, а внутренняя переменная y изменяется от функции
, образуя некую полосу на плоскости Oxy, а внутренняя переменная y изменяется от функции 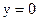 (горизонтальная прямая совпадающая с осью Ox), до функции
(горизонтальная прямая совпадающая с осью Ox), до функции  . (функция
. (функция  представляет из себя верхнюю дугу полуокружности с центром в начале координат и радиусом
представляет из себя верхнюю дугу полуокружности с центром в начале координат и радиусом  , что становиться очевидно если возвести функцию в квадрат). Обе функции могут быть построены по точкам.
, что становиться очевидно если возвести функцию в квадрат). Обе функции могут быть построены по точкам.

Таким образом получаем область:

Объединяя полученные области имеем:

Проецируя имеющуюся область на прямую Oy получаем отрезок [0;1], следовательно, пределы во внешнем интеграле будут изменяться от нуля до единицы. Что же касается изменение пределов во внутреннем интеграле, то находясь внутри области при уменьшении x мы упираемся в функцию  , а при увеличении x мы упираемся в функцию
, а при увеличении x мы упираемся в функцию  (или с учетом того что необходимо выразить x
(или с учетом того что необходимо выразить x  ). Таким образом получаем:
). Таким образом получаем:

8) Вычислить: 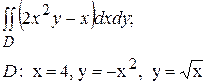
Для начала решения построим область D.

Для определения пределов интегрирования первым шагом спроецируем область на ось х, тем самым получив в качестве границ внешнего интеграла отрезок [0;4]. Двигаясь внутри области по прямым, параллельным оси Оу определяем какие функции выступают в качестве границ внутреннего интеграла. Таким образом имеем:

Данный интеграл вычисляем как повторный


Таким образом 
9) Вычислить: 
Будем вычислять тройной интеграл как повторный, аналогично предыдущему примеру.





