Подходя к физическим основам системы кровообращения, рассмотрим течение вязкой, смачивающей стенки жидкости по горизонтальной трубе постоянного сечения. При относительно невысокой скорости течение имеет ламинарный характер: слой молекул, прилегающий к стенке трубы, прилипает к ней и остается неподвижным. Следующий слой молекул под действием силы давления и при противодействии силы внутреннего трения между слоями смещается относительно пристеночного слоя и движется по отношению к стенкам трубы с некоторой небольшой скоростью. Каждый последующий слой молекул, смещаясь относительно предыдущего слоя, движется по отношению к стенке трубы с постепенно возрастающей скоростью, которая достигает наибольшего значения в центре трубы.
Математический анализ этого явления показывает, что распределение скоростей по сечению круглой трубы имеет параболический характер: 
Максимальная скорость в центре трубы 
. В этих формулах: 
— давления в начале и в конце участка трубы длиной 
- коэффициент вязкости
жидкости, R - радиус трубы и r- радиус рассматриваемого слоя
жидкости.
Ламинарное течение устанавливается в трубах с гладкими стенками, без резких изменений площади сечения или изгибов трубы, а так же при отсутствии множественных разветвлений. При нарушении этих условий и особенно при высоких скоростях течение переходит в турбулентное: скорости частиц жидкости при этом беспорядочно меняются, образуются местные завихрения - происходит перемешивание частиц жидкости.
Характерным для турбулентного течения являются местные изменения давления в жидкости, вызывающие колебательное движение частиц, сопровождающееся звуковыми явлениями (шум, журчание и т.п.), благодаря которым турбулентное течение легко обнаруживается. Турбулентное течение связано с дополнительными затратами энергии при движении жидкости, поэтому в кровеносной системе это может привести к дополнительной нагрузке на сердце. Шум возникающий при турбулентном течении крови, может быть использован для диагностики заболеваний. При поражении клапанов сердца возникают так называемые сердечные шумы, вызванные турбулентным течением крови. Турбулентное течение крови в аорте может быть вызвано, прежде всего, турбулентностью кровотока у входа в нее: вихри потока уже изначально существуют, когда кровь выталкивается из желудочка в аорту. У мест разветвления сосудов, а также при возрастании скорости кровотока течение может стать турбулентным и в артериях. Турбулентное течение может возникнуть в сосуде в области его локального сужения, например, при образовании тромба.
Скорость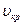 
перехода ламинарного течения в турбулентное можно определить, пользуясь определенным из опыта критерием – числом Рейнольдса Re (безразмерная величина), которое связывает ее с плотностью ρ, вязкостью 
жидкости и диаметром D трубы: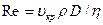 
. Для прямой гладкой трубы 
. Если 
, то течение переходит в турбулентное. От вязкости крови зависит ее течение по сосудам, которое может быть ламинарным или турбулентным. Ламинарное течение крови создает меньшую нагрузку на сердце, поскольку при нем работа сердца прямо пропорциональна объемной скорости кровотока, при турбулентном движении крови между этими параметрами устанавливается почти квадратичная зависимость (А~ Q1,8).
При течении реальной жидкости по горизонтальной трубе потенциальная энергия ее частиц расходуется на работу по преодолению внутреннего трения и поэтому статическое 
давление вдоль трубы постепенно падает. Для того чтобы обеспечить течение жидкости, необходимо в начале трубы создать давление, несколько превышающее падение давления вдоль всей трубы. В трубе постоянного сечения давление падает равномерно.
Пуазейль опытным путем установил, что средняя скорость 
ламинарного течения жидкости по неширокой горизонтальной круглой трубе постоянного сечения прямо пропорциональна разности давлений 
при входе и выходе из трубы, квадрату радиуса R трубы и обратно пропорциональна длине l трубы и коэффициенту вязкости жидкости (закон Пуазейля); 
В дальнейшем, используя рассмотренный выше закон распределения скоростей по сечению трубы, Гаген вывел эту формулу теоретически.
Средняя скорость течения жидкости определяет количество жидкости Q, протекающее через поперечное сечение S трубы в единицу времени: 
Следовательно, 
Эту формулу и называют обычно формулой Гагена — Пуазейля Ей можно придать и такой вид: 
, где 
Величину 
называют гидравлическим сопротивлением. Оно обратно пропорционально четвертой степени радиуса и поэтому весьма значительно возрастает с уменьшением радиуса трубы.
