Перейдем к более сложному случаю – заданию кривых в трехмерном пространстве. В случае функционального задания кривой  возможны многозначности в случае самопересечений и неудобства при значениях производных равных
возможны многозначности в случае самопересечений и неудобства при значениях производных равных  . Ввиду этого будем искать функцию в параметрическом виде. Пусть
. Ввиду этого будем искать функцию в параметрическом виде. Пусть  - независимый параметр, такой что
- независимый параметр, такой что  . Кубическим параметрическим сплайном назовем следующую систему уравнений:
. Кубическим параметрическим сплайном назовем следующую систему уравнений:

Координаты точек на кривой описываются вектором  , а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты
, а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты  :
:
 .
.
Одним из способов задания параметрического кубического сплайна является указание координат начальной и конечной точек, а также векторов касательных в них. Такой способ задания называется формой Эрмита. Обозначим концевые точки 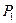 и
и  , а касательные векторы в них
, а касательные векторы в них  и
и  . Индексы выбраны таким образом с учетом дальнейшего изложения.
. Индексы выбраны таким образом с учетом дальнейшего изложения.
Будем решать задачу нахождения четверки коэффициентов  , так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна:
, так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна:
 ,
,  ,
,  ,
,  (*)
(*)
Перепишем выражение для  в векторном виде [3]:
в векторном виде [3]:

 .
.
Обозначим вектор строку  и вектор столбец коэффициентов
и вектор столбец коэффициентов 
 , тогда
, тогда  .
.
Из (*) следует, что  ,
,  . Для касательных
. Для касательных 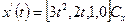 ,
, 
 ,
,
 . Отсюда получаем векторно-матричное уравнение:
. Отсюда получаем векторно-матричное уравнение:
 .
.
Эта система решается относительно  нахождением обратной матрицы размером
нахождением обратной матрицы размером  .
.
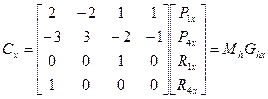 .
.
Здесь  - эрмитова матрица,
- эрмитова матрица, 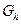 - геометрический вектор Эрмита. Подставим выражение
- геометрический вектор Эрмита. Подставим выражение  для нахождения
для нахождения  :
:  . Аналогично для остальных координат:
. Аналогично для остальных координат:  ,
, 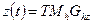 .
.
Выпишем в явном виде формулы для вычисления координат точек сплайна. Так как  , то умножая справа на
, то умножая справа на  , получаем:
, получаем:

 .
.
Четыре функции в скобках называются функциями сопряжения.
Форму кривой, заданной в форме Эрмита, легко изменять если учитывать, что направление вектора касательной задает начальное направление, а модуль вектора касательной задает степень вытянутости кривой в направлении этого вектора, как показано на рис. 42.
 |  | ||
Рассмотрим форму Безье, которая отличается от формы Эрмита способом задания граничных условий, а именно, вместо векторов
 и
и  вводятся точки (и соответствующие им радиус векторы)
вводятся точки (и соответствующие им радиус векторы)  и
и  , как показано на рис.43, такие что выполняются условия:
, как показано на рис.43, такие что выполняются условия: 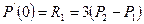 и
и  .
.
Переход от формы Эрмита к форме Безье осуществляется преобразованием:
 , (*)
, (*)
где  - геометрический вектор Безье. Подставляя это в выражение для
- геометрический вектор Безье. Подставляя это в выражение для  , получаем
, получаем
 .
.
Полезным свойством сплайнов в форме Безье является то что кривая всегда лежит внутри выпуклой оболочки, образованной четырехугольником  . Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице.
. Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице.
Заметим, что матрица вида
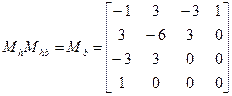 ‑ называется матрицей Безье.
‑ называется матрицей Безье.






