Приступая к изучению возможных схемных решений построения активных фильтров, необходимо уточнить некоторые понятия о фильтрах и отметить особенности их работы.
Фильтром нижних частот (ФНЧ) называют четырехполюсник, обеспечивающий пропускание сигналов низких частот и отсечку сигналов высоких частот, превышающих частоту среза фильтра (рис. 7.1, а). Фильтр верхних частот (ФВЧ) пропускает сигналы высоких частот и задерживает сигналы ниже частоты среза (рис. 7.1, б). Полосовой фильтр (ПФ) обеспечивает пропускание сигналов выше некоторой частоты, называемой нижней границей полосы пропускания, до частоты, называемой верхней границей полосы пропускания фильтра (рис. 7.1, в). Вне указанной полосы полосовой фильтр препятствует прохождению сигналов. Заградительным или режекторным фильтром (РФ) называют четырехполюсник, отсекающий сигналы выше некоторой частоты, определяющей нижнюю полосу заграждения, до частоты, определяющей верхнюю границу заграждения (рис. 7.1, г). Простейшие RС- цепи представляют собой Г-, П- и Т-образные пассивные фильтры нижних и верхних частот первого порядка. Используя последовательное или параллельное соединение этих фильтров можно реализовать полосовые и режекторные фильтры. Модуль коэффициента передачи пассивных фильтров в полосе пропускания меньше единицы, а крутизна частотной характеристики в полосе заграждения равна –20 дБ/дек. или –12 дБ/окт.
Активный фильтр содержит в своей структуре усилитель, охваченный положительной и отрицательной частотно-зависимыми обратными связями, благодаря которым увеличивается крутизна частотной характеристики в полосе заграждения, составляющая не менее –40 дБ/дек. или –24 дБ/окт. Крутизна частотной характеристики фильтра определяет угол наклона его амплитудно-частотной характеристики (АЧХ) в полосе заграждения. Ее можно определить используя соотношение
S = 20 log [| K (f 1)|/| K (f 2)|],
где |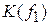 
| и | 
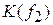| – соответственно модули коэффициентов передачи фильтра на частотах 
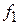и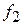 
. Для оценки крутизны S АЧХ фильтра в децибелах на декаду необходимо взять 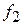= 10 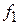, а для ее оценки в децибелах на октаву 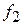= 2 .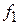
Частота среза 
фильтров определяется на уровне К = 0,707 (в логарифмической шкале – 6 дБ) относительно коэффициента передачи в полосе пропускания. Для ФНЧ полоса пропускания имеет границы [0, ], для ФВЧ – соответственно [ , µ], для ПФ – [ 
, 
], для РФ – [0, ] и [ , µ].
 |
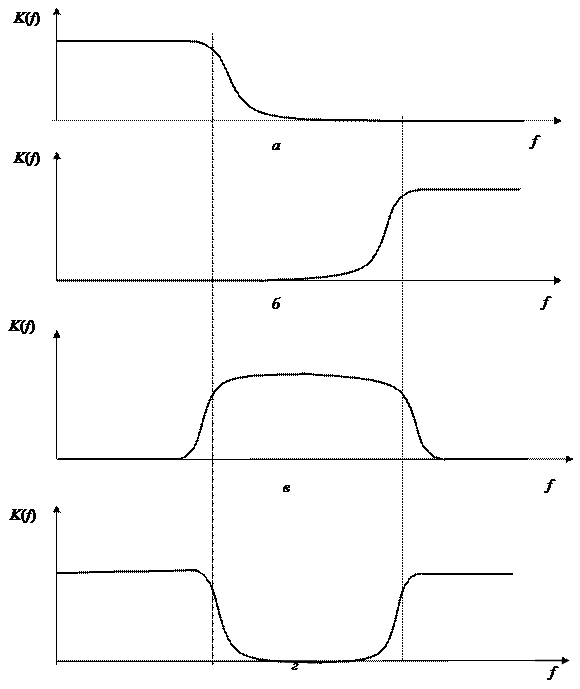Рис. 7.1. Частотные характеристики фильтров:
а – фильтр нижних частот; б – фильтр верхних частот; в – полосовой фильтр;
г – режекторный фильтр
Приведенные на рис. 7.1 АЧХ фильтров носят несколько упрощенный характер. В реальном случае фильтры различают по виду переходной характеристики (фильтры Баттерворта, Чебышева, Бесселя и др.).
Частотные свойства фильтров, в том числе и крутизна частотной характеристики, определяются их системной функцией. В зависимости от ее вида различают фильтры первого, второго и высших порядков.
Системная функция активного ФНЧ n -го порядка имеет вид
К (s) = К /(1 + a 1 s + a 2 s 2 +….+ ansn),
где К – коэффициент передачи на постоянном токе. Очевидно, что для фильтра первого порядка К (s) = К /(1 + RCs). Активные фильтры второго порядка строятся на основе схем усилительных устройств, в которых используются сложные частотно-зависимые цепи отрицательной или положительной обратной связи.
Предлагаемый для исследования в лабораторной работе вариант построения активного ФНЧ второго порядка с положительной обратной связью представлен на рис. 7.2, а. Передаточную функцию этого фильтра можно получить с использованием законов Кирхгофа. Она выглядит следующим образом:
К (s) = К / [1 + (3 – К) RCs + (RCs)2],
где коэффициент передачи в полосе пропускания определяется номиналами элементов отрицательной обратной связи: К = 1 + 
/ 
.
Частота среза фильтра 
определяется соотношением
= [ 
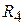
] – 1/2.
Для упрощения расчета фильтра обычно используют = = 
, =
= = 
.
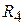Простой переменой мест задающих элементов и схема ФНЧ может быть преобразована в ФВЧ (рис. 7.2, б). Для этого фильтра коэффициент передачи в полосе пропускания К и частота среза будут определяться соотношениями: К = 1 + / , = [ ] – 1.
Следует отметить, что входные сопротивления фильтров зависят от частоты. Так, для ФНЧ (рис. 7.2, а) его входное сопротивление в полосе прозрачности 
= + + 
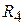®µ, а в полосе заграждения ® . Для ФВЧ входное сопротивление в полосе прозрачности ® , а в полосе заграждения ®µ.
Фильтры более высоких порядков можно построить каскадным соединением фильтров меньших порядков. Например, фильтр четвертого порядка можно создать с помощью последовательного соединения двух фильтров второго порядка. При этом системные функции перемножаются.
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
|
Рис. 7.2. Активные фильтры:
а – ФНЧ второго порядка; б – ФВЧ второго порядка; в – ФНЧ третьего порядка
Расчет фильтра нижних частот. Предлагается рассчитать ФНЧ Баттерворта третьего порядка с частотой среза = 3кГц (рис. 7.2, в). Параметры 
и 
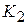– коэффициенты усиления соответствующих каскадов. Системная функция ФНЧ Баттерворта третьего порядка в соответствии с предложенными выражениями имеет вид
= [ /(s + 1)] [ 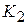/(s 2 +s + 1)],
где s – частота, нормированная к частоте среза 
= (RC)–1. Выбрав номинал С, определим номинал резистора R из выражения R = 1/( С). В соответствии с системной функцией фильтра второго порядка получим значение 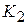.. Общий коэффициент усиления фильтра может быть выбран из условия ограниченности рабочей частоты пропускания операционных усилителей. Зададим, например, 
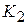= = 102. Тогда при = 50 частота среза = 3кГц попадает в полосу пропускания операционного усилителя.
Выбор значений номиналов резисторов и произволен. Однако для симметрии входных цепей обоих операционных усилителей обычно задают = || , + 
= 
|| 
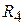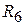. Следует также учесть, что сопротивления и не должны быть меньше предельно допустимой нагрузки для ОУ. Обычно и выбирают в диапазоне от 10 до 100 кОм, тогда сопротивления и рассчитывают исходя из обеспечения требуемого коэффициента передачи в полосе пропускания.
Порядок выполнения работы
1. Собрать на макетном поле фильтры нижних и верхних частот, используя схемы, приведенные на рис. 7.2, а, б. Номиналы элементов уточнить у преподавателя.
2. С помощью генератора гармонического сигнала исследовать АЧХ собранных фильтров. На входы фильтров подавать гармонический сигнал в частотном диапазоне от 1 Гц до 1 МГц с амплитудой 0,5 В.
3. Используя ранее собранные ФНЧ и ФВЧ, собрать на их основе ПФ и РФ.
4. С помощью генератора гармонического сигнала исследовать АЧХ ПФ и РФ и оценить частоты среза, крутизну частотной характеристики и коэффициент передачи в полосе прозрачности.
5. Собрать 2 фильтра нижних (верхних) частот, используя ранее приведенные схемы. Номиналы элементов уточнить у преподавателя. Последовательно соединив оба фильтра, снять суммарную АЧХ фильтра. Оценить крутизну частотной характеристики, суммарный коэффициент передачи, частоту (частоты) среза.
6. Рассчитать предложенный вариант схемы ФНЧ (ФВЧ) третьего порядка.
Содержание отчета
1. Схемы исследуемых устройств (ФНЧ, ФВЧ, ПФ и РФ).
2. Амплитудно-частотные характеристики исследованных активных фильтров.
3. Расчет ФНЧ (ФВЧ) третьего порядка с характеристикой Баттерворта.
4. Сравнительный анализ характеристик фильтров.
5. Предложения по альтернативному построению изученных фильтров.
Контрольные вопросы
1. В чем заключается сущность расчета фильтров?
2. Какие элементы фильтра влияют на коэффициент его передачи в полосе пропускания, а какие – на частоту среза?
3. Перечислите преимущества активных фильтров перед пассивными.
4. Укажите недостатки активных фильтров по отношению к пассивным.
5. Перечислите преимущества и недостатки активных фильтров Баттерворта, Чебышева и Бесселя.
6. Для решения каких задач используются ФНЧ, ФВЧ, ПФ и РФ?
7. Приведите схему фильтра Чебышева нижних (верхних) частот четвертого порядка и рассчитайте его элементы.
8. Что означает порядок фильтра?
9. Как построить полосовой фильтр с помощью ФНЧ и ФВЧ?
10. В чем недостатки ПФ с резонансной характеристикой по сравнению с ПФ, составленным путем последовательного соединения ФНЧ и ФВЧ?
11. Определите по виду АЧХ фильтра тип фильтра, его порядок и крутизну частотной характеристики.
Список рекомендуемой литературы
Манаев Е. И. Основы радиоэлектроники. М.: Сов. радио, 1976.
Шило В. Л. Линейные интегральные схемы. М.: Сов. радио, 1979.
Быстров Ю. А., Мироненко И. Г., Хижа Г. С. Электронные цепи и устройства. СПб.: Энергоатомиздат, 1999.
Опадчий Ю. Ф. Аналоговая и цифровая электроника. М.: Высш. шк., 2004.
Гусев В. Г. Электроника и микропроцессорная техника: Учеб. для вузов. М.: Высш. шк., 2004.
Степаненко И. П. Основы микроэлектроники: Учеб. пособие для вузов. М.: Лаб. базовых знаний, 2003.
Содержание
| Лабораторная работа № 1. Исследование усилителей сигналов на биполярных транзисторах…………………………………………………… | |
| Лабораторная работа № 2. Исследование усилителей сигналов на операционных усилителях……………………………………………………. | |
| Лабораторная работа № 3. Исследование автоколебательного и ждущего мультивибраторов на операционных усилителях…………………. | |
| Лабораторная работа № 4. Исследование генераторов гармонических сигналов на операционных усилителях………………………………….. | |
| Лабораторная работа № 5. Исследование устройств выборки-хранения и пиковых детекторов …………………………………………………….. | |
| Лабораторная работа № 6. Генераторы напряжения сигналов треугольной и линейной форм………………………………………………... | |
| Лабораторная работа № 7. Исследование особенностей работы активных фильтров………..………………………………………………. | |
| Список рекомендуемой литературы……………………………………… |
Редактор Э. К. Долгатов
___________________________________________________________
Подписано в печать. Формат 60х84 1/16. Бумага офсетная.
Печать офсетная. Гарнитура «Times». Печ. л. 3,0.
Тираж 245 экз. Заказ
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Издательство СПбГЭТУ «ЛЭТИ»
197376, С.-Петербург, ул. Проф. Попова, 5
