1. Построить таблицу истинности данной булевой функции.
2. Каждому единичному значению булевой функции будет соответствовать конъюнкция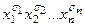 
, где 
- соответствующий набор значений перемен-ных. Конъюнкции соединяются знаком 
.
3. Заменить выражения 
по формуле: 
. Раскрыть скобки и привести подобные слагаемые по правилу: 
.
Пример. Построить СДНФ, СКНФ и полином Жегалкина для функции (11110011).
Таблица истинности данной булевой функции приведена на стр. 5.
СДНФ имеет вид:
.
СКНФ имеет вид:
.
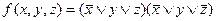Построим полином Жегалкина:
Примечание. Обратите внимание, что в [3] в представлении СДНФ и СКНФ в обозначении дизъюнкции вместо символа 
используется символ .
Замкнутые классы функций.
1. Класс 
функций, сохраняющих ноль.
.
2. Класс 
функций, сохраняющих единицу.
.
3. Класс S самодвойственных функций составляют функции, на противоположных наборах принимающие противоположные значения:
.
4. Класс М монотонных функций. Для двоичных векторов 
и 
, где 
, 
, вводится следующее отношение частичного порядка. Считается, что 
, если 
для . Класс M определяется следующим образом:
.
5. Класс линейных функций L составляют функции, которые представляются полиномом Жегалкина первой степени.
Проверка принадлежности булевой функции замкнутым классам 1-4 осуществляется по таблице истинности. Проверка принадлежности булевой функции классу L осуществляется путем построения полинома Жегалкина. Здесь 
– мно-жество всех булевых функций n переменных.
Функциональная полнота.
Система булевых функций называется функционально полной, если любая булева функция представляется супер-позицией (сложной функцией) функций данной системы.
Теорема Поста. Система булевых функций функ-ционально полна, если она не содержится целиком ни в одном из пяти замкнутых классов.
Для проверки функциональной полноты системы буле-вых функций строится так называемая таблица Поста, в которой отмечается принадлежность функций замкнутым классам. Если в каждом столбце таблицы Поста есть хотя бы один минус, система полна, в противном случае – нет.
Пример. Проверить функциональную полноту системы булевых функций 
.
Проверим принадлежность замкнутым классам функции 
. Построим таблицу истинности данной функции.
| 
| 
|
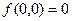, следовательно 
.
, следовательно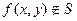 
.
, следовательно, 
.
, следовательно, 
.
Функция представляет собой полином Жегалкина первой степени, следовательно, 
.
Результаты можно занести в первую строку таблицы Поста. Остальные функции исследуются аналогично.
Построим таблицу Поста:
|
|
| S | M | L | |
|
| + | - | - | - | + |
| + | + | - | + | - |
| - | + | - | + | + |
В каждом столбце таблицы имеется минус, следовательно, система A функционально полна.
Минимальная функционально полная система называется базисом пространства булевых функций.
Элементы комбинаторики.
Основные задачи теории выборок. Формула включения и исклю-чения. Задача о беспорядках. Рекуррентные соотношения.
Литература: [1], с. 53-70; [5], пп. 5.1, 5.3, 5.5.
