Условимся обозначать через X независимую переменную, а через У — зависимую переменную. Зависимость величины У от X называется функциональной, если каждому значению величины X соответствует единственное значение величины У. Примеры функциональной зависимости нам хорошо известны из анализа.
При получении экспериментальных данных, на основе которых изучается зависимость У от X, часто имеет место влияние неконтролируемых случайных факторов, приводящее к тому, что каждому значению величины X соответствует не одно, а множество значений величины У. При этом неизвестно заранее, какое именно значение примет У. В этом случае У является случайной величиной. Величина X может быть как детерминированной (т.е. принимающей вполне определенные значения), так и случайной величиной. В последнем случае зависимость между X и называется стохастической или вероятностной.
Корреляционной зависимостью У от X называется функциональная зависимость группового среднего 
от х:
= 
Полученное уравнение называется уравнением регрессии У на Х; функция f(x) называется регрессией У на X, а ее график — линией регрессии У на X.
Аналогично определяется групповое среднее 
и корреляционная зависимость X от У.
Основными задачами теории корреляции являются:
1. Установление формы корреляционной зависимости (линейная, квадратичная, показательная и т.д.).
2. Оценка тесноты корреляционной зависимости.
Теснота корреляционной зависимости У от X оценивается по величине рассеяния значений У вокруг группового среднего . Большое рассеяние свидетельствует о слабой зависимости У от X, либо об отсутствии зависимости. Малое рассеяние указывает на наличие достаточно сильной зависимости.
Рассмотрим случай, когда между У и X существует линейная корреляционная зависимость, которую нарушают случайные факторы, проявляющиеся при измерении 2 У:
В качестве степени линейной связи двух величин У и X используется их выборочный коэффициент корреляции
..
где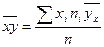 
, 
и 
-- выборочные средние величин X и У,
, 
, 
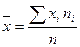— выборочные средние квадратические отклонения X и У,
, 
,
, 
,
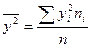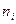— частоты величин X и У, п — объем выборки.
Коэффициент корреляции является безразмерной величиной (так как размерности числителя и знаменателя есть размерности произведения XY); его величина не зависит от выбора единиц измерения обеих величин. Величина rе меняется в пределах — 1 < rе < 1. Знак rе характеризует направление, а абсолютная величина rе — тесноту линейной корреляционной связи. Если rе > 0, то увеличение признака X в среднем приводит к увеличению признака У.
При этом, если rе — 0, то линейная корреляционная связь отсутствует (нелинейная корреляционная или функциональная связь при этом возможна) Если 
= 1, между X и У существует линейная функциональная зависимость, не искаженная действием случайных факторов.
Для качественной оценки тесноты корреляционной связи между X и У можно воспользоваться таблицей Чеддока:
| Диапозон изменения
| 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характер тесноты связи | слабая | умеренная | заметная | высокая | весьма высокая |
В силу того, что при любом статистическом исследовании на результатах неизбежно сказываются случайные ошибки, даже для независимых величин выборочный коэффициент корреляции может оказаться отличным от нуля. В связи с этим в процессе корреляционного анализа проверяется возможность опровержения гипотезы о некоррелированности рассматриваемых величин, т.е. проверяется значимость коэффициента корреляции.
Ход работы
Приводятся результаты 40 наблюдений над двумерной случайной величиной (Х, У). Требуется для каждой случайной величины Х и У:
1. Вычислить выборочный коэффициент корреляции.
2. Составить уравнения прямых регрессии и построить их.
Использовать результаты обработки статистических данных из лабораторных работ № 1,2.
Образец выполнения работы
Контрольные вопросы
1. Что называется функциональной зависимостью?
2. Что называется корреляционной зависимостью?
3. Сформулировать основные задачи теории корреляции.
4. По какой формуле вычисляется коэффициент корреляции?
5. Какой вид имеет уравнение прямой регрессии?
Рекомендуемая литература
1. Красс М.С. Математика для экономических специальностей. – М: ИНФРА – М, 1998
2. Ермаков В.И. Общий курс высшей математики (для экономистов). – М: ИНФРА – М, 2001
3. Кремер Н.Ш. Высшая математика для экономистов. – М: ЮНИТИ - 2000
4. Данко П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов: В 2 ч. Ч 1,2 – М.: ОНИКС 21 век, 2003
5. 7Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1972
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979
