Кодирование Методом Хаффмана

Растровая графика

Наиболее просто реализовать растровое представление. Растр, или растровый массив (bitmap), представляет совокупность битов, расположенных на сетчатом поле-канве Бит может быть включен (единичное состояние) или выключен (ну­левое состояние) Состояния битов можно использовать для представления чер­ного или белого цветов, так что, соединив на канве несколько битов, можно со­здать изображение из черных и белых точек.

Растровое изображение напоминает лист клет­чатой бумаги, на котором каждая клеточка закра­шена черным или белым цветом, в совокупности формируя рисунок, как показано на рис. 1.

Основным элементом растрового изображения является пиксел (pixel). Под этим термином часто понимают несколько различных понятий: отдель­ный элемент растрового изображения, отдельная точка на экране монитора, отдельная точка на изображении, напечатанном принтером. Поэтому на практике эти понятия часто обозначают так:

D пиксел — отдельный элемент растрового изоб­ражения;

О видеопиксел — элемент изображения на экра­не монитора;

О точка — отдельная точка, создаваемая прин­тером или фотонаборным автоматом

Цвет каждого пиксела растрового изображения — черный, белый, серый или любой из спектра — запоминается с помощью комбинации битов. Чем больше би­тов используется для этого, тем большее количество оттенков цветов для каждого пиксела можно получить Число битов, используемых компьютером для хранения информации о каждом пикселе, называется битовой глубиной или глубиной цвета.

Наиболее простой тип растрового изображения состоит из пикселов, имеющих два возможных цвета — черный и белый Для хранения такого типа пикселов требу­ется один бит в памяти компьютера, поэтому изображения, состоящие из пикселов такого вида, называются 1-битовыми изображениями. Для отображения большего количества цветов используется больше битов информации Число возможных и дос­тупных цветов или градаций серого цвета каждого пиксела равно двум в степени ко­личества битов, отводимых для каждого пиксела. 24 бита обеспечивают более 16 мил­лионов цветов. О 24-битовых изображениях часто говорят как об изображениях с естественными цветами, так как такого количества цветов более чем достаточно, чтобы отобразить всевозможные цвета, которые способен различать человеческий глаз

Основной недостаток растровой графики состоит в том, что каждое изображе­ние для своего хранения требует большое количество памяти. Простые растровые картинки, такие как копии экрана компьютера или черно-белые изображения, за­нимают до нескольких сотен килобайтов памяти.

Рис 1 Растровое изображение

 

Детализированные высококачественные рисунки, например, сделанные с помощью сканеров с высокой разреша­ющей способностью, занимают уже десятки мегабайтов. Для разрешения пробле­мы обработки объемных (в смысле затрат памяти) изображений используются два основных способа:

- увеличение памяти компьютера;

- сжатие изображений.

Другим недостатком растрового представления изображений является сниже­ние качества изображений при масштабировании.

Векторная графика

Векторное представление, в отличие от растровой графики, определяет описа­ние изображения в виде линий и фигур, возможно, с закрашенными областями, за­полняемые сплошным или градиентным цветом. Хотя это может показаться более сложным, чем использование растровых массивов, но для многих видов изображе­ний использование математических описаний является более простым способом.

В векторной графике для описания объектов используются комбинации ком­пьютерных команд и математических формул для описания объектов. Это позво­ляет различным устройствам компьютера, таким как монитор и принтер, при ри­совании этих объектов вычислять, где необходимо помещать реальные точки.

Векторную графику часто называют объектно-ориентированной или чертеж­ной графикой. Имеется ряд простейших объектов или примитивов, например, эллипс, прямоугольник, линия. Эти примитивы и их комбинации используются для создания более сложных изображений. Если посмотреть содержание файла векторной графики, обнаруживается сходство с программой. Он может содержать команды, похожие на слова и данные в коде ASCII, поэтому векторный файл мож­но отредактировать с помощью текстового редактора. Приведем в условном упро­щенном виде команды, описывающие окружность:

объект — окружность;

центр — 50, 70; радиус — 40;

линия: цвет — черный, толщина — 0,50;

заливка — нет.

Данный пример показывает основное достоинство векторной графики — опи­сание объекта является простым и занимает мало памяти. Для описания этой же окружности средствами растровой графики потребовалось бы запомнить каждую отдельную точку изображения, что заняло бы гораздо больше памяти.

Кроме того, векторная графика в сравнении с растровой имеет следующие пре­имущества:

- простота масштабирования изображения без ухудшения его качества;

- независимость объема памяти, требуемой для хранения изображения от выб­ранной цветовой модели.

Недостатком векторных изображений является их некоторая искусственность, заключающаяся в том, что любое изображение необходимо разбить на конечное множество составляющих его примитивов.

 

Растровая и векторная графика существуют, не обособлено друг от друга. Так, векторные рисунки могут включать в себя и растровые изображения. Кроме того, векторные и растровые изображения могут быть преобразованы друг в друга — в этом случае говорят о конвертации графических файлов в другие форматы. До­статочно просто выполняется преобразование векторных изображений в растро­вые. Не всегда осуществимо преобразование растровой графики в векторную, так как для этого растровая картинка должна содержать линии, которые могут быть идентифицированы программой конвертации (типа CorelTrace в составе пакета CorelDraw) как векторные примитивы. Это касается, например, высококачествен­ных фотографий, когда каждый пиксел отличается от соседних.

Разрешающая способность

Разрешающая способность — это количество элементов в заданной области. Этот термин применим ко многим понятиям, например, таким как:

- разрешающая способность графического изображения;

- разрешающая способность принтера как устройства вывода;

- разрешающая способность мыши как устройства ввода.

Например, разрешающая способность лазерного принтера может быть задана 300 точек на дюйм (dpi — dot per inche), что означает способность принтера напеча­тать на отрезке в один дюйм 300 отдельных точек. В этом случае элементами изоб­ражения являются лазерные точки, а размер изображения измеряется в дюймах.

Разрешающая способность графического изображения измеряется в пикселах на дюйм. Отметим, что пиксел в компьютерном файле не имеет определенного размера, так как хранит лишь информацию о своем цвете. Физический размер пик­сел приобретает при отображении на конкретном устройстве вывода, например, на мониторе или принтере.

Разрешающая способность технических устройств по-разному влияет на вы­вод векторной и растровой графики.

Так, при выводе векторного рисунка используется максимальное разрешение устройства вывода. При этом команды, описывающие изображение, сообщают устройству вывода положение и размеры какого-либо объекта, а устройство для его прорисовки использует максимально возможное количество точек. Таким об­разом, векторный объект, например, окружность, распечатанная на принтерах раз­ного качества, имеет на листе бумаги одинаковые положение и размеры. Однако более гладко окружность выглядит при печати на принтере с большей разрешаю­щей способностью, так как состоит из большего количества точек принтера.

Значительно большее влияние разрешающая способность устройства вывода оказывает на вывод растрового рисунка. Если в файле растрового изображения не определено, сколько пикселов на дюйм должно создавать устройство вывода, то по умолчанию для каждого пиксела используется минимальный размер. В случае лазерного принтера минимальным элементом служит лазерная точка, в монито­ре — видеопиксел. Так как устройства вывода обличаются размерами минимального элемента, который может быть ими создан, то размер растрового изображе­ния при выводе на различных устройствах также будет неодинаков.

Цвета

Некоторые предметы видимы потому, что излучают свет, а другие — потому, что его отражают. Когда предметы излучают свет, они приобретают тот цвет, ко­торый видит глаз человека. Когда предметы отражают свет, то их цвет определя­ется цветом падающего на них света и цветом, который эти объекты отражают. Излучаемый свет выходит из активного источника, например, экрана монитора. Отраженный свет отражается от поверхности объекта, например, листа бумаги.

Существуют два метода описания цвета: система аддитивных и субтрактивных цветов.

Система аддитивных цветов работает с излучаемым светом. Аддитивный цвет получается при объединении разноцветных лучей света. В системе используются три основных цвета: красный, зеленый и синий (Red, Green, Blue — RGB); При смешивании их в разных пропорциях получается соответствующий цвет. Отсут­ствие этих цветов представляет в системе черный цвет. Схематично смешение цветов показано на рис. 2 a.

В системе субтрактивных цветов происходит обратный процесс: какой-либо цвет получается вычитанием других цветов из общего луча света. При этом белый цвет получается в результате отсутствия всех цветов, а присутствие всех цветов дает черный цвет. Система субтрактивных цветов работает с отраженным цветом, например, от листа бумаги. Белая бумага отражает все цвета, окрашенная — неко­торые поглощает, остальные отражает.

В системе субтрактивных цветов основными являются голубой, пурпурный и желтый цвета (Cyan, Magenta, Yellow — CMY) — противоположные красному, зеленому и синему. Когда эти цвета смешивают на бумаге в равной пропорции, получается черный цвет. Этот процесс проиллюстрирован на рис. б. В связи с тем, что типографские краски не полностью поглощают свет, комбинация трех

а) б)

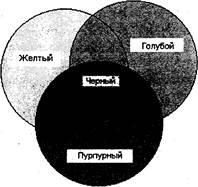
Рис. 2. Система смешения цветов

 

Масштабирование векторных рисунков выполняется просто и без потери каче­ства. Так как объекты векторной графики создаются по их описаниям, то для из­менения масштаба векторного объекта, достаточно изменить его описание. На­пример, чтобы увеличить в два раза векторный объект, следует удвоить значение, описывающее его размер

Масштабирование растровых рисунков является намного более сложным процес­сом чем для векторной графики и часто сопровождается потерей качества. При изме­нении размеров растрового изображения выполняется одно из следующих действий

- одновременное изменение размеров всех пикселов (в большую или мень­шую сторону);

- добавление или убавление пикселов из рисунка для отражения производи­мых в нем изменений, называемое выборкой пикселов в изображении

Простейший способ изменения масштаба растрового рисунка состоит в изме­нении размера всех его пикселов. Так как внутри самого рисунка пикселы не име­ют размера и приобретают его уже при выводе на внешнее устройство, то измене­ние размера пикселов растра в сильной степени похоже на масштабирование векторных объектов — необходимо сменить только описание пиксела, а осталь­ное выполнит устройство вывода.

Устройство вывода для создания пиксела определенного физического размера ис­пользует столько своих минимальных элементов (лазерных точек — для лазерного прин­тера, видеопикселов —для монитора), сколько сможет. При масштабировании изобра­жения количество входящих в него пикселов не меняется, а изменяется количество создаваемых устройством вывода элементов, идущих на построение отдельного пиксела изображения. На рисунке показан пример масштабирования растрового изображения — увеличения его в два раза по каждому измерению

Выборка растрового рисунка может быть сделана двумя различными способами

Во-первых, просто дублируется или удаляется необходимое количество пиксе­лов. При этом в результате масштабирования, как правило, ухудшается качество изображения. Например, при увеличении размера рисунка возрастают его зернис­тость и дискретность. При умень­шении размера рисунка потери в качестве не столь заметны, однако при последующем восстановлении уменьшенного рисунка до прежне­го размера опять возрастают зерни­стость и дискретность. Это связано с тем, что при уменьшении размера рисунка часть пикселов была уда­лена из исходного изображения и потеряна безвозвратно, а при пос­ледующем восстановлении разме­ров рисунка недостающие пикселы дублировались из соседних.

 

Во-вторых, с помощью определенных вычислений можно создать пикселы дру­гого цвета, определяемого цветами первоначального пиксела и его окружения. Этот метод называется интерполяцией и является более сложным, чем простое дублирование. При интерполяции, кроме дублируемых пикселов, отбираются и соседние с ними, с помощью которых вновь создаваемые пикселы получают от существующих усредненный цвет или оттенок серого. В результате переходы меж­ду пикселами становятся более плавными, что позволяет убрать или уменьшить эффект пилообразности изображения.

Сжатие изображений

Как и многая информация, графика может быть сжата. Это выгодно с точки зрения экономии памяти компьютера, так как, например, высококачественные изображения имеют размеры до нескольких десятков мегабайтов. Для файлов гра­фических изображений разработано множество схем и алгоритмов сжатия, основ­ными из которых являются следующие:

- групповое сжатие,

- кодирование методом Хаффмана,

- сжатие по схеме LZW,

- арифметическое сжатие,

- сжатие с потерями,

- преобразование цветов RGB в цвета YUV

В основе большинства схем сжатия лежит использование одного из следую­щих свойств графических данных: избыточность, предсказуемость и необязатель­ность. В частности, групповое кодирование (RLE) основано на использовании пер­вого свойства. Кодирование по методу Хаффмана и арифметическое кодирование, основанные на статистической модели, используют предсказуемость, предлагая более короткие коды для более часто встречающихся пикселей. Алгоритмы сжа­тия с потерями основаны на избыточности данных.

Следует учесть, что алгоритм, обеспечивающий большую степень сжатия, обыч­но более сложный и поэтому требует для распаковки данных больше процессор­ного времени.

Рассмотрим подробнее несколько алгоритмов сжатия.

Групповое сжатие

Групповое сжатие представляет собой одну самых простых схем сжатия фай­лов. Суть его заключается в том, что серия повторяющихся величин заменяется единственной величиной и ее количеством. На примере можно заметить выгоду в длине между «aabbbbbbbcdddeeeeaaa» и «2a7blc3d4e3a». Данный алгоритм прост в реализации и хорошо сжимает графические файлы с большими однотонными областями. Групповое кодирование используется во многих форматах растровых файлов таких как TIFF, PCX и т. д.

Кодирование Методом Хаффмана

Смысл метода Хаффмана заключается в замене данных более эффективными кодами. Более короткие коды используются для замены более часто появляющих­ся величин. Например, в выражении abbbcccddeeeeeeeeef есть шесть уникальных величин, с частотами появления: а:1, b:3, c:3, d:2, e:9, f:l. Для образования мини­мального кода используется двоичное дерево. Алгоритм объединяет в пары эле­менты, появляющиеся наименее часто, затем пара объединяется в один элемент, а их частоты объединяются. Это действие повторяется до тех пор, пока элементы не объединятся в пары. В данном примере надо объединить а и f — это первая пара, а присваивается 0 ветвь, а f— 1-я.,Это означает, что 0 и 1 будут младшими битами кодов для а и f соответственно. Более старшие биты будут получены из дерева по мере его построения

' Суммирование частот дает в итоге 2. Два — теперь самая низкая частота, по­этому пара а и f объединяется с d (которая тоже имеет частоту 2). Исходной паре присваивается 0-я ветвь, ad — ветвь 1. Таким образом, код для а заканчивается на 00; для f— на 01, d заканчивается на 1 и будет на один бит короче по сравнению с кодами для а и f.

Дерево продолжает строится подобным образом так, что наименее распростра­ненные величины описываются более длинными кодами. Данное кодирование нуждается в точной статистике, выражающейся в том, как часто каждая величина появляется в файле. Следовательно, для работы по схеме Хаффмана необходимы два этапа: на первом этапе создается статистическая модель, на втором — кодиру­ются данные. Следует отметить, что компрессия и декомпрессия по Хаффману — достаточно медленный процесс.

Форматы графических файлов

Краткая информация о графических файлах приведена в таблице 21.1.

Таблица 21.1 Типы графических файлов

Название	Тип	Использование	Фирма	Платформы	Расширение
BMP	Растровый	Хранение и отображе­ние информации в среде Windows	Microsoft	PC	bmp
GIF	Растровый	Передача данных в сети CompuServe	Compu­Serve Inc.	PC, UNIX	gif
PCX	Растровый	В графических редакторах	Zsoft Corp.	PC	pcx-
JPEG	Растровый	Для фотографической ' информации	Joint Photographic Experts Group	PC, Macintosh	jpg
Название	Тип	Использование	Фирма	Платформы	Расширение
TIFF	Растровый	Обмен данными между настольными и изда­тельскими системами	Aldus Corp.	PC, Macintosh, UNIX	tif
DXF	Векторный	Обмен чертежами и данными САПР	Autodesk Inc.	PC	dxf
CDR	Векторный	Чертежная, издательская и другие виды графики	Corel	PC	cdr
WMF	Векторный	Хранение и отображение информации в среде Windows	Microsoft	PC	wmf
RIB	Векторный	Передача информации об объектах	Pixar	PC, Macintosh, UNIX	rib

 

Рассмотрим структуру файлов изображений типа BMP и TIFF, получивших наиболее широкое распространение на практике.