1. Критерий оптимизации транспортной задачи:
а) минимум затрат на продукцию;
б) удовлетворение всех затрат потребителей;
в) максимум прибыли;
г) минимум затрат на доставку продукции.
2. Необходимое и достаточное условие решения транспортной задачи в области допустимых решений:
а) сумма запасов больше суммы заявок;
б) количество пунктов запаса равно количеству пунктов потребителей; 
в) сумма запасов равна сумме заявок;
г) ацикличность.
3. Транспортная задача
| Заявки Запасы | 300+в | ||
| к+в | |||
закрыта при к равном: а) 100; б) 300; в) 600; г) 400.
4. В транспортной задаче m поставщиков n потребителей, тогда число переменных равно:
а) m + n; б) m × n; в) m + n - 1; г) n.
5. Если 
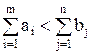 в транспортной задаче, то для ее решения следует ввести: а) фиктивного поставщика; б) фиктивного потребителя;
в транспортной задаче, то для ее решения следует ввести: а) фиктивного поставщика; б) фиктивного потребителя;
в) фиктивного поставщика и потребителя; г) сij=0.
6. В транспортной задаче m поставщиков и n потребителей, тогда ограничения по запасам:
а) 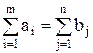 ; б)
; б) 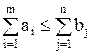 ;
;
в) 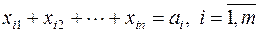 ;
;
г)  .
.
7. В транспортной задаче (m поставщиков и n потребителей) вводят фиктивного поставщика, если:
а)  ; б)
; б) 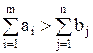 ;
;
в) 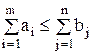 ; г)
; г) 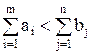 .
.
8. В транспортной задаче (m поставщиков и n потребителей) вводят фиктивного потребителя, если:
а)  ; б)
; б) 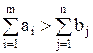 ;
;
в) 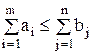 ; г)
; г) 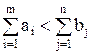 .
.
9. Если в транспортной задаче (m поставщиков и n потребителей) ограничения по потребностям имеют вид  , то:
, то:
а) суммарных запасов больше, чем суммарных потребностей;
б) суммарных запасов меньше, чем суммарных потребностей;
в) суммарных запасов не меньше, чем суммарных потребностей;
г) суммарных запасов не больше, чем суммарных потребностей.
10. В транспортной задаче (m – число поставщиков n – число потребителей) ранг системы ограничений равен:
а) m + n; б) m × n; в) m + n - 1; г) n.
11. Опорное решение системы ограничений транспортной задачи должно иметь базисных переменных:
а) m + n; б) m + n - 1; в) m × n; г) mn - 1.
12. Особенности системы ограничений математической модели закрытой транспортной задачи:
а) коэффициенты при всех неизвестных по 1;
б) каждая переменная встречается только в двух уравнениях;
в) система уравнений транспортной задачи симметрична относительно всех переменных  ;
;
г) матрица, составленная из коэффициентов при переменных  , состоит из единиц и нулей, причем каждый столбец матрицы содержит два элемента равных 1, а остальные – 0;
, состоит из единиц и нулей, причем каждый столбец матрицы содержит два элемента равных 1, а остальные – 0;
д) все ответы верны;
13. Метод нахождения оптимального плана закрытой транспортной задачи:
а) Фогеля; б) северо-западного угла;
в) потенциалов; г) минимального элемента.
14. Опорный план закрытой транспортной задачи содержит свободных переменных:
а) m + n - 1; б) mn - 1; в) mn; г) mn - (m + n - 1).
15. Математическая модель, соответствующая транспортной таблице
| Заявки Запасы | |||
имеет вид:
а) 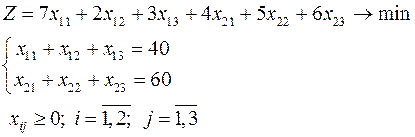
б) 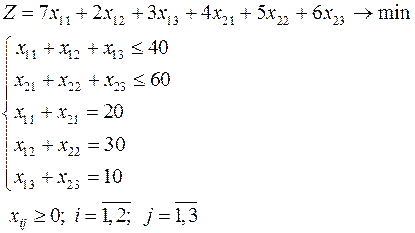
в) 
г) 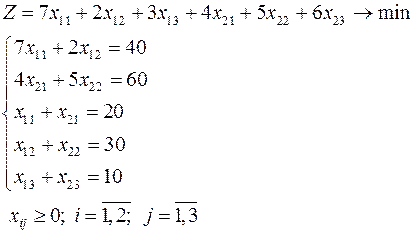 .
.
16. Математической модели транспортной задачи
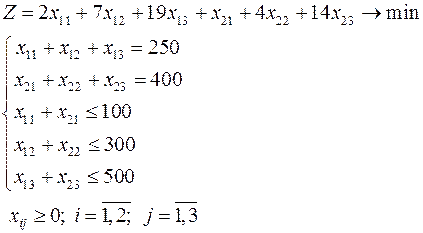
соответствует транспортная таблица:
а)
| Заявки Запасы | ||||||
б)
| Заявки Запасы | ||||
в)
| Заявки Запасы | ||||||
г) а, в – верно; д) б, в – верно.
17. Количество занятых клеток поставщиками в оптимальном плане транспортной задачи (m поставщиков и n потребителей) равно:
а) m + n; б) m × n; в) m + n - 1; г) количеству поставщиков.
18. Условия оптимальности плана закрытой транспортной задачи:
а) сумма платежей за доставку единицы груза не больше тарифа в свободных клетках транспортной таблицы;
б) сумма платежей за доставку единицы груза не меньше тарифа, в занятых клетках транспортной таблицы;
в) сумма платежей за доставку единицы груза равна тарифу в занятых и не больше в свободных клетках транспортной таблицы;
г) сумма платежей за доставку единицы груза меньше тарифа в свободных и больше в занятых.
19. План транспортной задачи (m поставщиков и n потребителей) оптимальный, если в транспортной таблице:
а) 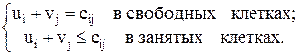
б) 
в) 
г) 
20. Цикл транспортной таблицы (m поставщиков и n потребителей) в закрытой транспортной задаче -
а) замкнутая ломаная, вершины которой в занятых клетках;
б) замкнутая ломанная, в вершинах которой поворот на 90o;
в) замкнутая ломанная, с вершинами в занятых клетках, в которых совершается поворот на 90o;
г) нет верного ответа.
21. Цикл перепоставки необходим в транспортной задаче (m поставщиков и n потребителей), если:
а) переплата в свободных клетках;
б) занято поставками клеток m + n -1;
в)  ; г)
; г) 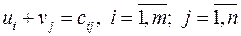 .
.
22. В транспортной задаче на сети из n пунктов количество базисных ребер равно:
а) m + n; б) m + n - 1; в) (n - 1)(m - 1); г) n - 1.
23. План поставок в транспортной таблице
| Заявки Запасы | ui | ||||||
| vj |
является: а) оптимальным; б) вырожденным;
в) опорным; г) недопустимым.
24. По заданным в таблице значениям потенциалов
| Заявки Запасы | ui | ||||||
| -2 | |||||||
| vj |
опорное решение равно: а) 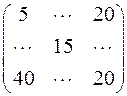 ; б)
; б) 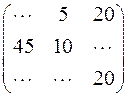 ;
;
в) 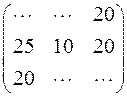 ; г)
; г)  .
.
25. В транспортной задаче на сети цикл перепоставок строится по ребрам:
а) свободным; б) базисным; в) занятым;
г) б, в – верно; д) а,б – верно.
26. В транспортной задаче на сети (m поставщиков и n потребителей) решение оптимально, если оценки 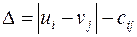 свободных ребер:
свободных ребер:
а) больше 0; б) не больше 0; в) меньше 0; г) равны 0.
27. Необходимое условие разрешимости транспортной задачи (m поставщиков и n потребителей) с ограничениями на пропускную способность:
а) 
 б)
б) 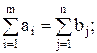
в) 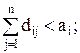 г)
г) 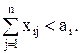
28. Достаточное условие разрешимости транспортной задачи (m поставщиков и n потребителей) с ограничениями на пропускную способность:
а)  б)
б) 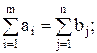
в) 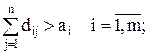 ;
;
г) существование хотя бы одного допустимого решения.
29. Для оптимального решения транспортной задачи с ограничениями на пропускную способность необходимо и достаточно существование потенциалов ui (i=  ) и vj (j=
) и vj (j= 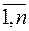 ) таких, что выполняются условия
) таких, что выполняются условия
для клеток:
а) 
б) 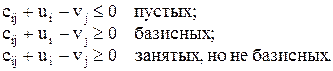
в) 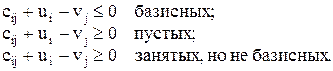
г) 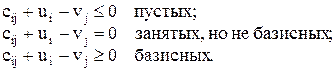
30. Оптимальный план транспортной задачи
| Заявки Запасы | ui | ||||||
| -2 | |||||||
| -1 | |||||||
| vj |
равен:
а) 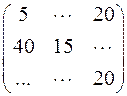 ; б)
; б) 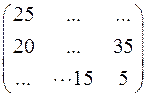 ; в)
; в)  .
.
ПРАКТИКУМ
Задание 1. Составить базу данных ТЗ, состоящей из четырех пунктов производства с аi количеством запаса, пяти пунктов потребления с b j количеством заявок и Cij транспортными расходами на перевозку из Ai пункта отправления в Bj пункт назначения.
Составить математическую модель ТЗ, двойственную к ней. Решить исходную ТЗ вручную методом потенциалов. Объяснить экономический смысл двойственных оценок.
Задание 2. Пиломатериал (ai) необходимо перевезти с трех разных баз четырем клиентам (bj) с минимальными затратами на доставку, если известна стоимость доставки единицы груза – числитель  от i –той базы
от i –той базы 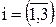 j – тому клиенту
j – тому клиенту 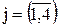 и ограничения на пропускную способность транспортных средств - знаменатель
и ограничения на пропускную способность транспортных средств - знаменатель 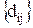 . Решить задачу методом потенциалов.
. Решить задачу методом потенциалов.
Варианты заданий
| bj ai | bj ai | |||||||||
| 15/15 | 20/13 | 16/14 | 18/13 | 22/14 | 27/15 | 23/14 | 26/16 | |||
| 32/13 | 45/16 | 30/17 | 32/15 | 30/15 | 29/16 | 28/17 | 30/16 | |||
| 19/14 | 22/16 | 21/15 | 23/17 | 31/16 | 35/14 | 33/17 | 32/15 |
| bj ai | bj ai | |||||||||
| 17/13 | 19/13 | 21/14 | 18/15 | 20/14 | 25/15 | 23/14 | 24/16 | |||
| 23/15 | 27/14 | 28/16 | 30/15 | 33/15 | 30/16 | 28/17 | 31/16 | |||
| 29/15 | 32/16 | 30/15 | 33/16 | 32/16 | 33/14 | 30/17 | 31/15 |
| bj ai | bj ai | |||||||||
| 16/15 | 22/17 | 18/15 | 19/16 | 22/15 | 26/15 | 25/14 | 25/16 | |||
| 30/13 | 45/16 | 30/17 | 30/15 | 25/15 | 28/16 | 27/17 | 31/16 | |||
| 20/14 | 22/16 | 22/15 | 24/17 | 30/16 | 33/14 | 33/16 | 34/15 | |||
| bj ai | bj ai | |||||||||
| 13/15 | 18/16 | 20/17 | 15/19 | 20/15 | 26/14 | 21/17 | 25/16 | |||
| 28/14 | 35/18 | 30/17 | 30/15 | 30/15 | 29/16 | 28/17 | 29/16 | |||
| 17/13 | 21/16 | 20/15 | 24/17 | 31/16 | 35/14 | 30/17 | 33/13 |
| bj ai | bj ai | |||||||||
| 17/15 | 21/13 | 15/14 | 19/13 | 27/14 | 28/15 | 25/14 | 25/16 | |||
| 32/14 | 47/16 | 30/17 | 33/15 | 31/15 | 30/16 | 28/16 | 30/16 | |||
| 19/13 | 22/17 | 20/15 | 23/17 | 16/16 | 40/14 | 33/17 | 32/15 |
| bj ai | bj ai | |||||||||
| 13/15 | 19/13 | 16/13 | 18/13 | 19/14 | 27/16 | 23/14 | 26/17 | |||
| 30/13 | 43/17 | 30/16 | 31/14 | 30/15 | 28/16 | 28/17 | 30/15 | |||
| 25/18 | 21/16 | 21/17 | 23/16 | 31/16 | 35/14 | 33/19 | 32/13 |
| bj ai | bj ai | |||||||||
| 17/14 | 21/13 | 15/14 | 19/14 | 28/16 | 28/15 | 25/14 | 25/16 | |||
| 32/12 | 47/16 | 31/17 | 32/15 | 31/14 | 29/16 | 28/16 | 30/16 | |||
| 19/15 | 22/17 | 20/16 | 23/17 | 16/16 | 40/13 | 33/17 | 29/15 |
| bj ai | bj ai | |||||||||
| 13/14 | 19/13 | 15/14 | 19/13 | 27/14 | 28/15 | 23/4 | 25/7 | |||
| 31/14 | 43/16 | 30/17 | 32/15 | 31/15 | 30/16 | 28/7 | 30/14 | |||
| 19/13 | 22/17 | 20/15 | 21/18 | 16/16 | 40/15 | 33/16 | 32/13 |
| bj ai | bj ai | |||||||||
| 17/15 | 21/13 | 15/14 | 19/13 | 27/14 | 28/15 | 25/14 | 25/16 | |||
| 32/14 | 47/16 | 30/17 | 33/15 | 31/15 | 30/16 | 28/16 | 30/16 | |||
| 19/13 | 22/17 | 20/15 | 23/17 | 16/16 | 40/14 | 33/17 | 32/15 | |||
| bj ai | bj ai | |||||||||
| 20/15 | 21/12 | 23/14 | 21/17 | 30/14 | 28/15 | 21/14 | 25/16 | |||
| 33/14 | 45/16 | 32/17 | 36/19 | 33/15 | 29/16 | 28/16 | 24/16 | |||
| 21/17 | 25/15 | 26/19 | 25/21 | 16/20 | 40/15 | 33/22 | 32/15 |
МОДУЛЬ 6. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
В задачах динамического программирования находится ряд оптимальных решений последовательно для каждого этапа, обеспечивающих оптимальное развитие всего процесса в целом.
Динамическое программирование – это метод, приспособленный для решения оптимизационных задач, связанных с многошаговыми, поэтапными процессами.
Многошаговый процесс можно интерпретировать так: весь цикл разбивается на этапы и на каждом этапе требуется принять то или иное решение.
При решении задач методом ДП вводят функцию Беллмана fk, которая представляет собой максимальную эффективность многошагового процесса, состоящего из k шагов.
Для вычисления функции Беллмана составляется, так называемое, функциональное уравнение Беллмана, позволяющее находить значение функции Беллмана fk+1, если известно fk.
При выводе уравнения Беллмана используется та или иная форма принципа оптимальности. Одной из наиболее общих формулировок является: если на первом шаге принято решение, то дальнейшее решение принимается таким образом, чтобы за оставшееся число шагов достичь максимального (минимального) результата.






