Задача №1. Построить недостающие проекции точек на поверхности цилиндра.
Методические рекомендации по выполнению задания.
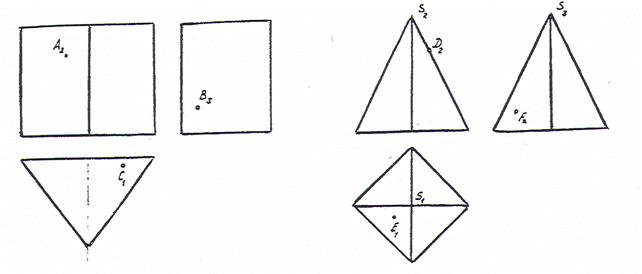
Цилиндр является проецирующей поверхностью, т.е. все точки, лежащие на боковой поверхности цилиндра спроецируются по линиям связи на очерк, т.е. на окружность. Точка А – видимая, потому она проецируются на часть окружности, расположенную перед очерковыми образующими. Точка В – невидимая, следовательно, она проецируется на часть окружности за очерковыми образующими. Точка С расположена на верхнем основании цилиндра, таким образом, проецируем точку С с П1 на П2 по линии связи.
Задача №2. Построить три проекции точки А на конической поверхности.
Методические рекомендации по выполнению задания.
Проекция точки А имеется только на фронтальной плоскости проекции. Чтобы построить проекцию точки А на горизонтальной плоскости замерим радиус параллели, на которой расположена А2, и построим вторую проекцию параллели (окружность) на П1, затем по линии определяем проекцию А1. Для построения проекции точки А на П3 замеряем расстояние y на П1 и переносим данное расстояние по линии связи на П3.
Задача №3.
Через точку К провести плоскость, параллельную прямой m.
Даны плоскость m (m1; m2) и точка К (К1; К2). Чтобы провести через К плоскость 
параллельную прямой, достаточно изобразить на комплексном чертеже проходящие через точку К фронтальную а 2, и горизонтальную а 1 проекции прямой а, параллельные соответствующим проекциям заданной прямой m, а далее провести через т. К произвольную прямую b (решений бесконечное множество).
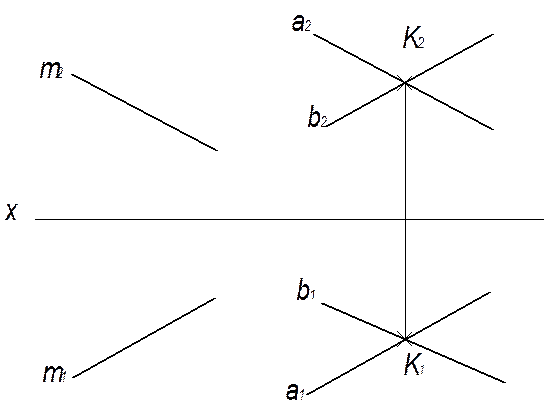
Типовое контрольное задание
Найти недостающие проекции точек на поверхностях.
2. Тема 4 «Графопозиционные задачи. Правила построения линии пересечения двух поверхностей».
Модуль – графопозиционные задачи.
Ключевые слова: линия пересечения, плоскость-посредник, сфера-посредник, проецирующая поверхность.
Самостоятельная работа по данному разделу начинается с изучения способов построения точки пересечения прямой и плоскости и построения линии пересечении плоскостей и поверхностей.
Вопросы для изучения теоретической части темы
1) Алгоритм построения линии пересечения прямой и плоскости.
2) К чему сводится задача на построение линии пересечения гранного геометрического тела с телом вращения.
3) Какая фигура получается при пересечении призмы плоскостью.
4) В каких случаях применяются в качестве посредников плоскости?
5) Когда применяются сферы посредников?
Тесты
1. Как строят линию пересечения двугранных геометрических тел.
а) задача сводится к методу плоскостей посредников;
б) задачи сводится к построению линии пересечения двух плоскостей и построению точки пересечения прямой и плоскости;
в) задача сводится к методу сфер-посредников.
2. К чему сводится задача на построение линии пересечения гранного геометрического тела с телом вращения.
а) к построению линии пересечения: плоскости с поверхностью вращения и к построению точки пересечений прямой с поверхность вращения.
б) к методу плоскостей посредников.
в) к методу сфер-посредников.
3. В каких случаях применяются в качестве посредников сферы.
а) во всех случая построения и пересечения поверхностей.
б) при проецирующих поверхностях.
в) при не проецирующих поверхностях тел вращения, если оси их пересекаются.
