Через две точки пространства можно провести единственную прямую. Следовательно, чтобы задать прямую на чертеже, надо задать проекции двух её точек и соединить одноименные проекции этих точек.
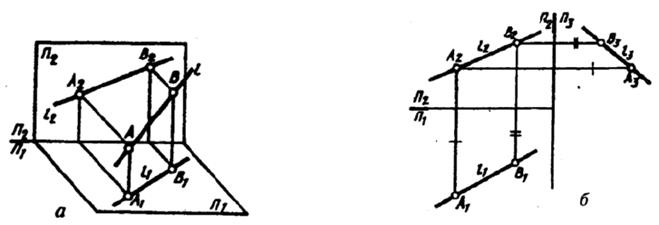
Рис 4.
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из плоскостей проекций (рис. 4), называют прямой общего положения. Прямую параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частого положения.
Линии уровня – прямые, параллельные одной из плоскостей проекций.
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой уровня или горизонталью (рис. 5а).
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой уровня или фронталью (рис. 5б).
Прямая, параллельная профильной плоскости проекций, называется профильной прямой уровня (рис. 5в).
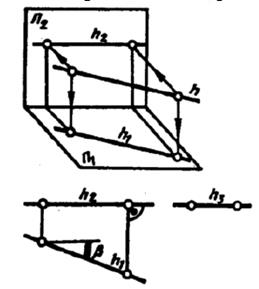
а) б)
в)
Рис.5
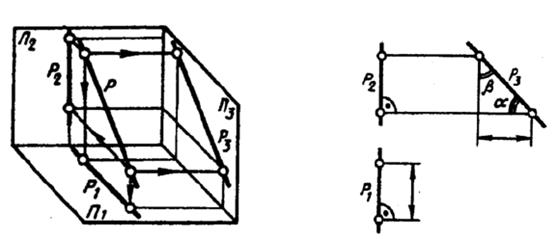
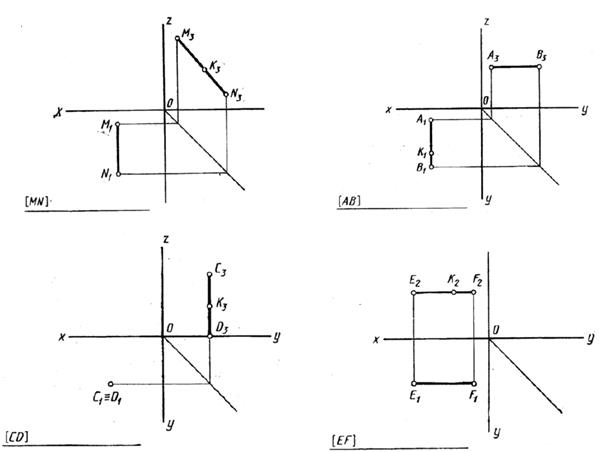
Проецирующие прямые – прямые перпендикулярные к плоскостям проекций. Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD), профильно проецирующие прямые (ЕF)(рис. 6).
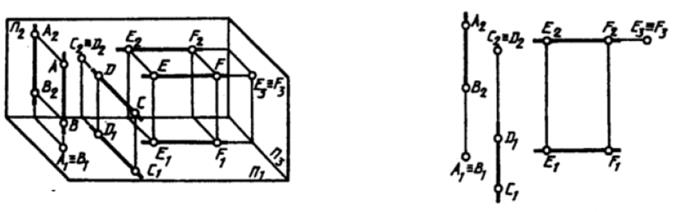
Рис. 6
Взаимное расположение двух прямых
Две прямые могут иметь различное расположение. Они могут быть параллельными (с и d), пересекаться (m и n) и скрещиваться (k и l) (рис. 7).
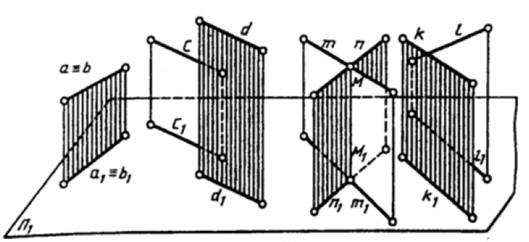
Рис. 7
На рисунке 8 приведены комплексные чертежи: а – параллельных прямых; б – пересекающихся прямых; в и г – скрещивающихся прямых.
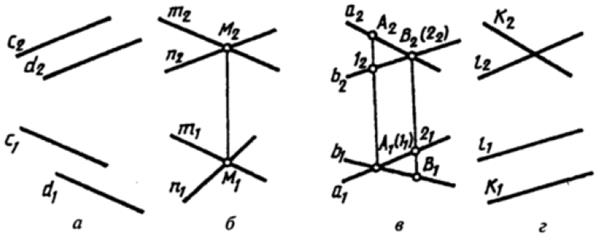
Рис. 8
Задача 8. Постройте третью проекцию отрезка на чертеже. Постройте недостающие проекции точки К, принадлежащей отрезку. Укажите расположение отрезков в пространстве.
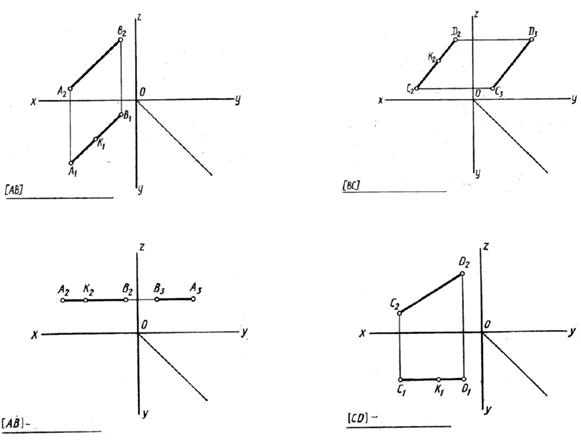
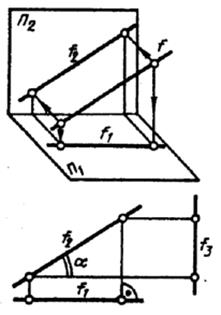
Определение натуральной величины отрезка прямой общего положения
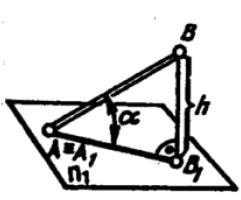
Натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на любую плоскость проекции, а другой катет равен разности расстояний концов отрезка до той же плоскости проекций;
Угол наклона отрезка прямой к той же плоскости проекций, на которой выполнено построение, равен углу между катетом-проекцией и гипотенузой.
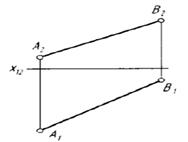Возьмем отрезок общего положения АВ (рис. 9) и определим его натуральную величину и угол наклона к горизонтальной плоскости проекций (рис. 10а) и угол наклона к фронтальной плоскости проекций (рис. 10б).
Рис. 9
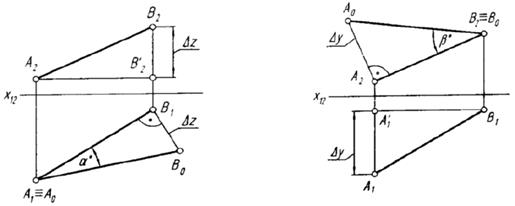
а б
Рис. 10
Задача 9. Даны две точки А(60; 40; 5) и В(30;20;30). Постройте проекции прямой, определите натуральную величину отрезка и углы наклона к плоскостям проекций П1 и П2, П3.
