Горловка, 2010
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Внешнюю обложку тетради следует оформить в соответствии с общими требованиями оформления учебного заведения.
Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью. Для замечаний преподавателя нужно на каждой странице оставлять поля.
В контрольной работе 15 вариантов. Номер варианта студент выбирает в соответствии со следующей таблицей
| № вар. | |||||||||||||||
| № в журнале | |||||||||||||||
Перед выполнением каждой контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и может воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Т е м а 1. Введение и анализ функции одной переменно й
При изучении этой темы обратите внимание на понятие функции, способы задания функции, основные элементарные функции.
Центральными понятиями в этой теме являются понятия предела переменной величины, предела функции и понятие непрерывной функции. При решении задач на вычисление пределов функции обратите внимание на то, что в определении предела функции не учитывается значение функции в предельной точке, другими словами, величина 
не зависит от величины 
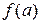. Значение 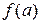может и не существовать. Отсюда следует, что под знаком предела можно производить тождественные преобразования выражения, не принимая во внимание его поведение в предельной точке. В частности, под знаком предела можно производить сокращение дроби на множитель, обращающийся в нуль в предельной точке (но не равный нулю вблизи этой точки).
Вопросы для самопроверки
1. Что такое переменная величина?
2. Сформулируйте определение функции. Что называется областью определения функции?
3. Какие способы задания функции Вы знаете?
4. Какие функции называются элементарными?
5. Сформулируйте понятие предела переменной величины.
6. Дайте определение понятия предела функции.
7. Какая функция называется ограниченной?
8. В каком случае функция называется бесконечно малой?
9. Сформулируйте основные теоремы о пределах.
10. Дайте определение непрерывности функции в точке.
11. Укажите основные свойства непрерывных функций.
Т е м а II. Производная и дифференциал
При изучении этой темы обратите внимание на определение производной, ее геометрическое и механическое истолкование. Особую роль при решении задач играет правило вычисления производной сложной функции.
При дифференцировании некоторых функций нередко значительно упрощает вычисление прием, состоящий в том, что перед вычислением производной функцию предварительно логарифмируют (см. [2], §12).
Вопросы для самопроверки
1. Сформулируйте определение производной.
2. Каков геометрический смысл производной?
3. Что называется касательной к кривой? Напишите уравнение касательной к графику функции 
4. Каков механический смысл первой и второй производной?
5. Каковы правила вычисления производных от суммы, произведения, частного двух функций?
6. Сформулируйте правило вычисления производной сложной функции.
7. Что называется дифференциалом функции?
8. Чем отличается дифференциал функции от ее приращения?
Т е м а III. Исследование поведения функций
Изучение этой темы следует начать с усвоения понятий возрастания и убывания функции, максимума и минимума функции, выпуклости и вогнутости кривой.
Обратите внимание на следующие обстоятельства:
1) функция, определенная на отрезке, может достигать максимума и минимума только при значениях х, заключенных внутри рассматриваемого отрезка;
2) не следует считать, что максимум и минимум функции являются соответственно ее наибольшим и наименьшим значениями на рассматриваемом отрезке (например, в точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума).
При решении задач на построение графика функции следует учесть, что приведенный в формулировке задач № 61 – 80 порядок исследования
функций может быть нарушен, так знание одних свойств функции позволяет сделать вывод о других ее свойствах. Так, например, если при исследовании точек разрыва функции выяснено, что односторонние пределы функции в некоторой точке бесконечны, то это означает наличие в этой точке вертикальной асимптоты графика.
Иногда целесообразно намечать элементы графика параллельно с исследованием функции.
Вопросы для самопроверки
1. Как формулируется теорема Лагранжа?
2. Каковы признаки возрастания и убывания функции?
3. Докажите, что функция у = соs х – х убывает в любом промежутке.
4. Сформулируйте правила нахождения экстремумов функции.
5. Приведите пример, показывающий, что обращение в нуль производной не является достаточным условием экстремума функции.
6. Как найти интервалы выпуклости, вогнутости, точки перегиба кривой?
7. Покажите, что график функции 
не имеет точек перегиба, каковы бы ни были значения а и b.
8. Дайте определение асимптоты кривой. Как найти вертикальные и наклонные асимптоты графика функции?
Т е м а 1У. Применение правил отыскания наибольших и наименьших значений к решению задач
При решении задач этой темы следует иметь в виду, что наибольшее и наименьшее значения функция достигает либо на концах заданного отрезка, либо в тех его внутренних точках, которые являются критическими точками первого рода этой функции (точками, подозрительными на экстремум).
КОНТРОЛЬНАЯ РАБОТА
Задание 1. Найти указанные пределы.
Решение типовых примеров.
При подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида «
». Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
где х1,х2 – корни квадратного трехчлена 
У нас
так как дискриминант квадратного трехчлена 
а следовательно, 
Аналогично
Теперь условие примера можно переписать в другом виде и продолжить решение:
Здесь сталкиваемся с неопределенностью 
избавиться от которой можно вынесением за скобки в числителе и знаменателе старшей степени переменной:
В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:
Решение примера будет выглядеть следующим образом:
Задание 2. Найти производные 
, пользуясь правилами и формулами дифференцирования.
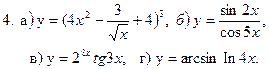
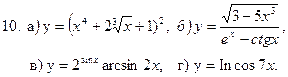
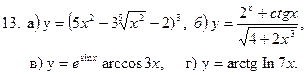
Решение типовых примеров. При решении всех последующих примеров кроме таблицы производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции:
г) если задана сложная функция 
где 
то есть функция 
если каждая из функций и дифференцируемая по своему аргументу, то
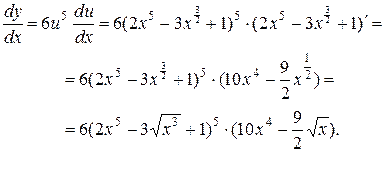
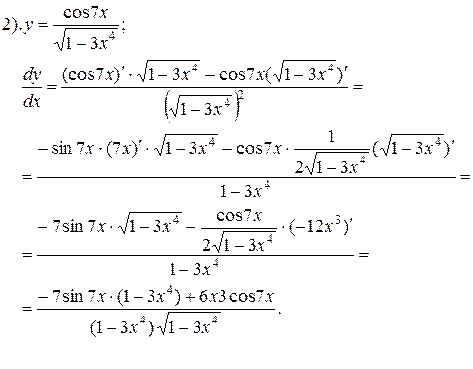
Задание 3. задан закон s(f) изменения пути движенияматериальной точки. Требуется найти значения скорости и ускорения этой точки в момент времени t0.
| 1. | 
|
| 2. | 
|
| 3. | 
|
| 4. | 
|
| 5. | 
|
| 6. | 
|
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
| 11. | 
|
| 12. | 
|
| 13. |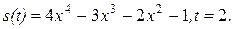 
|
| 14. |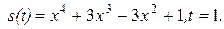 
|
| 15. | 
|
Решение типового примера.
Пусть 
Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент первой и второй производных функции, задающей закон изменения пути движения точки.
У нас
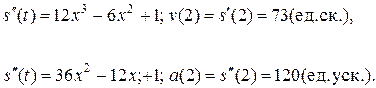
Задание 4. Исследовать заданные функции методами дифференциального исчисления начертить их графики. Исследование функций и построение графиков рекомендуется проводить последующей схеме:
1) Найти область определения функции D(y); 2) исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва; 3) найти точки экстремума функции и определить интервалы ее монотонности; 4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика; 5) найти асимптоты графика функции; 6) построить график, используя результаты предыдущих исследований; 7) для функции из пункта а) найти дополнительно наибольшее и наименьшее значения на отрезке 
.
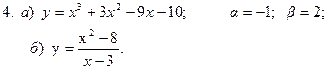
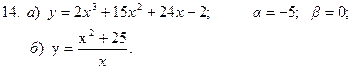
Решение типовых примеров.
1) Областью определения данной функции являются все действительные значения аргумента х, то есть D (у): 
а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода х1 = –5, x2 = –1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
| 
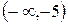
| −5 | (−5, −1) | −1 | 
|
| + | − | + | ||
| & | max | ( | min | & |
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку 2 рода х = –3. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
|
| 
| −3 | 
|
| − | + | |
|
| Ç | т.п. | È |
Значение х = − 3 является абсциссой точки перегиба графика функции, а ордината этой точки
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты y=kx+б воспользуемся формулами
Имеем
Таким образом, у графика заданной функции наклонных асимптот нет.
5) Для построения графика в выбранной системе координат изобразим точки максимума А1(–5; 4), минимума А2 (–1; –4), перегиба А3 (–3; 0) и точку пересечения графика с осью Оy A4 
С учетом результатов предыдущих исследований построим кривую (см. рис. 2).
6) Найдем наибольшее и наименьшее значения заданной функции на отрезке [ – 3; 0]. Для этого посчитаем значения функции на концах этого отрезка, в критических точках 1 рода, попавших на отрезок, и сравним результаты:
Очевидно,
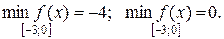
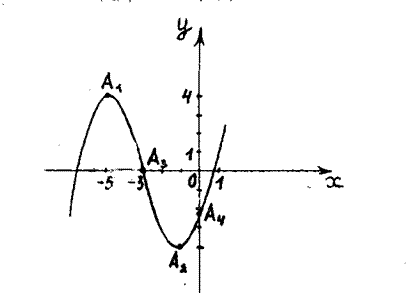
Рис.2.
2. 
1) Область определения.
2) Исследование на непрерывность и классификацию точек разрыва.
Заданная функция непрерывна всюду, кроме точки х = 4.
Вычислим ее односторонние пределы в этой точке:
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 − вертикальной асимптотой графика.
3) Исследование на экстремум и промежутки монотонности.
|
|
| −2 | (−2, 4) | (4, 10) |
| ||
|
| + | − | Не сущ. | − | + | ||
|
| & | max | ( | ( | min | & |
4) Исследование графика на выпуклость, вогнутость, точки перегиба.
Так как 
, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
|
| 
| 
| |
|
| − | Не сущ. | + |
|
| Ç | È |
5) Исследование графика на наличие наклонных асимптот.
Таким образом, прямая y = x+ 4 − наклонная асимптота графика.
6) Построение графика.
Очевидно график заданной функции пересекает ось Оy в точке (0;−5) и на основе обобщения результатов всех предыдущих исследований имеет вид, представленный на рис. 3.
Рис.3
