Правило Крамера
Обозначим
(определитель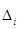 
получается из D заменой i -го столбца на столбец свободных членов). Правило Крамера состоит в том, что при 
СЛАУ совместна и имеет единственное решение 
Решение СЛАУ методом Гаусса
При решении методом Гаусса расширенную матрицу 
системы элементарными преобразованиями приводят к трапецеидальному виду. Затем, начиная с последнего уравнения, последовательно находят неизвестные.
К числу элементарных преобразований относят:
1) перестановку столбцов или строк;
2) умножение столбца (строки) на число, отличное от нуля;
3) прибавление к столбцу (строке) другого столбца (другой строки), умноженного предварительно на некоторое число;
4) зачеркивание нулевого столбца (строки).
Трапецеидальной матрицей называется матрица 
имеющая вид
где 
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия.
1. Решить систему по правилу Крамера:
1) 
Решение. Находим главный определитель системы:
. Следовательно, система имеет единственное решение. Формулы Крамера:
, 
, 
.
Вычислим определители 
, 
, 
.
.
В главном определителе первый столбец заменили столбцом свободных членов.
.
.
В главном определителе второй столбец заменили столбцом свободных членов.
.
В главном определителе третий столбец заменим столбцом свободных членов.
.
Находим 
, 
, 
.
; 
; 
.
2) 
Ответ. 1) 
;
2) 
.
2. Решить СЛАУ методом Гаусса:
1)
Запишем расширенную матрицу системы и выполним эквивалентные преобразования. В результате получим:
.
Последней матрице соответствует система линейных уравнений треугольного вида, т.е имеет единственное решение:
Получим решение системы:
Метод последовательного исключения неизвестных предусматривает, что переменные можно исключать в любом порядке.
.
Последней матрице соответствует система линейных уравнений:
2) 
Запишем расширенную матрицу системы и выполним эквивалентные преобразования. В результате получим:
.
В последней матрице отбросили нулевую строку. Запишем систему линейных уравнений, соответствующую последней матрице:
Эта система является совместной и неопределенной. Перенесем одно неизвестное, например 
, в правую часть последнего уравнения системы, получим решение:
Неизвестному можно придать любые значения, поэтому система имеет бесчисленное множество решений.
Рассуждая в терминах строчного ранга матрицы, можно заключить, что ранг матрицы системы равен 3 (число ненулевых строк после применения к ней метода Гаусса), а количество свободных неизвестных равно 
(n-число неизвестных системы).
3) 
Выполнив над системой эквивалентные преобразования, получим:
.
Получим систему:
Получили противоречивый результат 
. Система несовместна (ранг расширенной матрицы, равный 4, оказался больше ранга матрицы системы, равный 3).
4) 
.
Ответ. 1) 
; 2) 
;
3) Система несовместна; 4) 
.
Задания для самостоятельного решения
1. Решить СЛАУ по правилу Крамера, методом Гаусса, матричным методом:
1) 
2) 
3) 
5) 
6) 
7) 
8) 
9) 
Ответ.
2. Решить систему уравнений:
1) 
2) 
3) 
4) 
Ответ. 1) 
; 2) 
;
3) 
; 4) 
.
