Понятие о спектральном анализе

До этого момента мы с вами занимались измерением интегральных оценок вибрационных сигналов, таких как общий уровень или уровень в полосе. Эти оценки давали нам представление о суммарной колебательной энергии процесса, сосредоточенной в выбранной полосе частот. В целом ряде задач вибродиагностики этого вполне достаточно, но для точной идентификации источников колебаний желательно иметь полное представление о колебательном процессе т.е. его спектр [23]. Для иллюстрации этого утверждения мы приведем вам следующий пример. Представьте себе, что вы наблюдаете за приближающейся группой людей. Сначала вы можете только констатировать тот факт, что вы видите людей. По мере приближения группы вы начинаете различать отдельные фигуры и уже в состоянии определить их число. Наконец, когда они подойдут к вам достаточно близко, вы сможете определить их пол или даже узнать в них своих знакомых. Этот пример показывает, что по мере увеличения подробностей, которые вы имеете при наблюдении, вы можете все точней идентифицировать наблюдаемый объект или явление.

В спектральном анализе исследуются периодические модели вибрации. Цель анализа – разложить сложное колебание (Рис. 58) с циклическими компонентами (поскольку силы, вызывающие вибрацию, преимущественно состоят из периодических составляющих, к которым подмешен широкополосный шум) на несколько основных гармоник с определенными частотами, на которых сосредоточен максимум энергии колебаний. В результате спектрального анализа можно обнаружить всего несколько повторяющихся циклов различной частоты в интересующих вас сигналах, которые, на первый взгляд, выглядят как случайный шум.

 

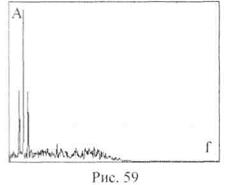
Спектры графически представляются в виде зависимостей амплитуды гармонических составляющих вибрации от их частоты (Рис. 59). Спектры бывают дискретными и непрерывными. Дискретный спектр содержит небольшое число отдельных гармонических составляющих, имеющих достаточно большую амплитуду. В непрерывном спектре мы видим плавно меняющуюся, непрерывную зависимость амплитуды колебания от частоты.

 

 

Для того, чтобы выполнить спектральный анализ используют специальные приборы - виброанализаторы. Большинство цифровых анализаторов для получения спектров используют Быстрое Преобразование Фурье (БПФ). БПФ работает с выборками сигнала,

равными по длине 2ⁿ, где n - целое число. Обычно п равно 9-11, т.е. длина выборок равна 512 - 2048 отсчетам. Выборки такой длины позволяют разбить анализируемый частотный диапазон на 200 - 800 полос. Все гармонические составляющие, попадающие в каждую из полос, будут приводиться к некоторому среднему значению, отражаемому на спектре. Таким образом, разрешение (точность) r [Гц/лин] спектрального анализа определяется как отношение верхней анализируемой частоты f _в[Гц] к числу полос спектрального анализа N [Лин].

Рассмотрим пример. Пусть нам нужно получить спектр сигнала, верхняя частота которого равна f _в =100 Гц. разрешение анализа r =0.5 Гц/лин., или, что тоже самое, 200 линиям в спектре. Тогда для наших приборов F[24]=256 Гц, длина выборки должна быть N=512 точек: время одного цикла измерения составит Т=512*1/256=2 секунды. Этот пример показывает, что не стоит увлекаться повышением точности спектрального анализа. Во-первых, это приводит к увеличению времени измерения (в нашем примере оно составляет 2 секунды только для одного измерения, добавьте к этому время настройки АРУ и усреднения и вы получите достаточно приличное время измерения) это относится к любому анализатору. Во-вторых, точность 0.5 Гц/лин достаточна для решения практически всех задач вибродиагностики. Все же, если вам необходимо сократить время измерения, то для этого существуют два способа, увеличить верхнюю частоту анализа или уменьшить число линий в спектре (понизить разрешение анализа).

 

Понятие о спектральном анализе

Оценка состояния агрегатов с использованием спектрального анализа

В линейных механических системах, с которыми мы имеем дело, частота возмущающей силы совпадает с частотой реакции системы на эту силу. Этот факт позволяет нам идентифицировать источник вибрации.

Большинство дефектов имеют жесткую связь с частотой вращения роторов агрегата и (или) режимами его работы. Исследуя зависимость изменения спектрального состава вибрации от вышеупомянутых факторов, и сравнивая ее с вибрацией нормального[25] агрегата, можно сделать вывод о причинах повышенной вибрации. При этом нужно учесть один немаловажный факт.

 

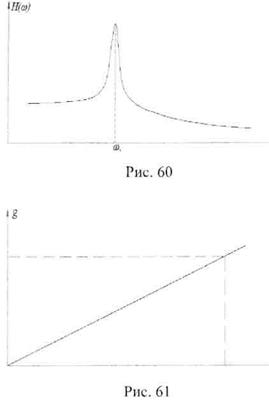
Механическая система похожа на фильтр, имеющий полосы пропускания и среза. Гак, обычная масса на пружине имеет один резонанс, определяемый жесткостью пружины и величиной массы. В дорезонансной области рассмотренная система обладает высокой чувствительностью к возмущающей силе, а в зарезонансной она существенно ослабляет возмущающую силу. По сути, масса на пружине является низкочастотным фильтром. Поэтому изменение вибрации агрегата может быть вызвано двумя факторами: изменением возмущающих сил Р(1) или отклонением механических свойств агрегата Н(г) (в нашем примере, жесткости пружины). Мы с вами имеем вибродиагностическую задачу, в которой нам известна контурная вибрация g(t), по которой мы должны определить и устранить источник вибрации (силу). Очевидно, что эта задача не имеет однозначного решения. Поэтому для получения достоверных результатов при диагностике нужно учитывать это. Механические свойства системы или ее передаточная функция Н(f) может быть определена при помощи записи зависимости вибрации оборотной частоты от частоты вращения агрегата на выбеге (скоростной). По сути, скоростная характеристика и есть передаточная функция, полученная при воздействии на машину дисбалансов, неизбежно присутствующих на машине.

 

Модуляция

Итак, что же такое модуляция? Модуляция это изменение по заданному закону во времени величин, характеризующих колебательный процесс. Мы с вами знаем три основных величины, характеризующих колебание. Это частота, амплитуда и фаза. В механике наибольшее распространение получила именно амплитудная модуляция. При амплитудной модуляции в уравнении гармонического колебания амплитуда так же является функцией времени. Необходимым условием амплитудной модуляции служит существенное отличие по частоте модулирующей функции от частоты «несущей[26]». Частота несущей должна быть во много раз больше частоты модулирующей функции.

 

 

 

 

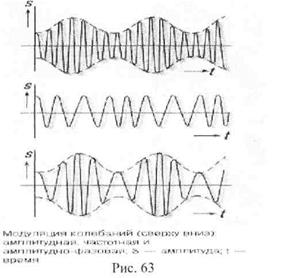
Другие виды модуляции сигнала изображены на Рис. 63. Хочется обратить особое внимание на один из видов фазовой модуляции вибросигнала, возникающий при биениях. Биениями называют почти гармонические колебания, амплитуда А(1) является колеблющейся функцией времени с квазипериодом, большим по сравнению с квазипериодом 2p/ w несущего колебательного процесса. В простейшем случае биения можно получить при наложении двух гармонических колебаний с близкими частотами w₁ и w₂ (Рис. 64):

 

 

 

 

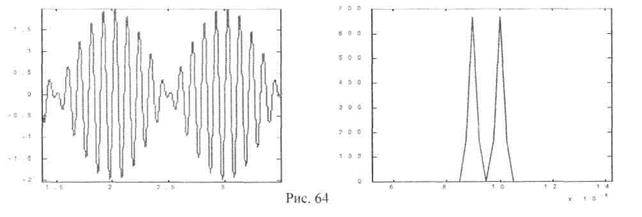
Понятие об огибающей

В машинах возникает ряд вибрационных процессов, сопровождающихся колебаниями энергии. Другими словами, колебательный процесс может иметь непостоянную амплитуду вибрации. Примером таких процессов могут служить биения. Биения возникают при сложении вибрации машин, имеющих несколько отличающиеся друг от друга частоты вращения (1-2 Гц), при условии их плохой виброизоляции друг от друга.

На Рисунке 65 показана вибрация 50 Гц машины при наличии биений, в разных масштабах времени и вибрация машины при отсутствии биений. На рисунках хорошо видно, что вибрационный процесс имеет переменную амплитуду колебаний или так называемую «огибающую».

Подобные нестационарные вибрационные процессы могут возникать и по другим причинам Наиболее яркий пример - возникновение амплитудной модуляции в подшипнике качения при наличии подвижных дефектов. При вращении дефект поочередно проходит то через нагруженную зону (вибрация возрастает), то через разгруженную (вибрация уменьшается). Амплитудная модуляция возникает также, например, в зубчатой передаче. В ней, при вращении, возникает амплитудная модуляция частоты зацепления оборотными частотами шестерни и колеса (при наличии на них дефектов).

 

 

 

Ясно, что для того, чтобы исследовать огибающую вибросигнала, нужно прибегнуть помощи специальной технологии ее выделения. Суть технологии заключается в следующем. В сложном вибрационном сигнале выделяется узкая полоса частот, ширина которой обычно составляет 1/3 октавы[27] (f₂/f₁»1,26). Необходимость такой фильтрации объясняется тем, что нужно настроится на вибрацию, вызываемую интересующим нас дефектом.

Для пояснения этого факта уместна следующая аналогия. Настройка на дефект происходит также как на радиостанцию в приемнике. В эфире (вибрация машины) присутствуют одновременно сигналы от множества радиостанций (различные источники вибрации), и если мы будем принимать их одновременно, то, очевидно, что мы ничего не сможем разобрать в принимаемой информации. Но если мы настроимся на конкретную частоту, на которой вещает интересующая нас станция «диагностируемый дефект), то без труда сможем обнаружить ее и насладится любимой музыкой (определить степень развития дефекта).

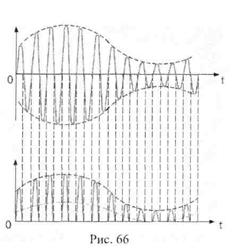
После выполнения третьоктавной фильтрации, из высокочастотного вибрационного сигнала выделяют огибающую с помощью процедуры детектирования (от лат. detection – обнаружение). Для этого сигнал выпрямляют и подвергают низкочастотной фильтрации.

Низкочастотная фильтрация нужна для устранения высокочастотных пульсаций от несущей частоты. На Рис. 66 сверху показаны колебания с амплитудной модуляцией на входе детектора, а снизу представлен выпрямленный сигнал и сигнал, прошедший через фильтр низких частот.

На заключительном этапе выделения огибающей устраняют постоянную составляющую вибрации, которая равна среднему значению уровня вибрации в анализируемой полосе частот. Далее сигнал подвергают обычной обработке измеряют его пик-фактор, или определяют его спектральный состав.

Последовательность выделения огибающей сигнала представлена на Рис. 67.

 

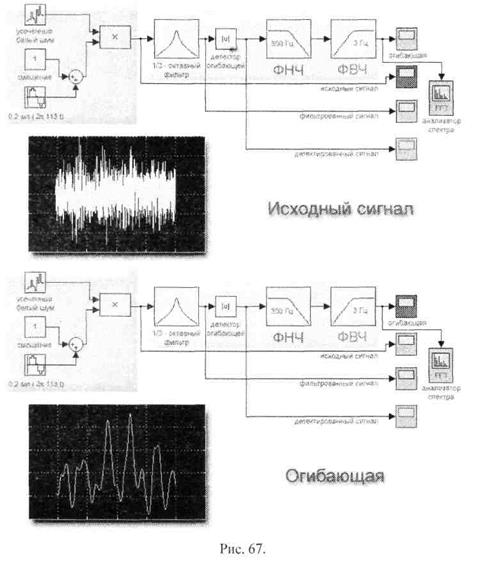
Понятие о неуравновешенности

 

Настал черед поговорить о балансировке. Так что же это такое. Классическое определение балансировки гласит: балансировка это уравновешивание (устранение дисбаланса) вращающихся частей машин. Дисбаланс (от дис[28]... и баланс[29]), в свою очередь, есть неуравновешенность вращающихся частей машин, она возникает при несовпадении оси, проходящей через центры опорных поверхностей цапф изделия, с его главной центральной осью инерции (в большинстве случаев - это ось симметрии ротора). Более правильным на наш взгляд, было бы называть балансировку компенсацией дисбалансов, так как, при балансировке мы не устраняем исходные дисбалансы, ведь почти всегда их положение на роторе остается неизвестным, а компенсируем их влияние на вибрацию ротора корректирующими массами, устанавливаемыми в плоскости коррекции. Давайте подробнее поговорим о дисбалансе. Дисбаланс D[г·мм] равен произведению неуравновешенной массы т на расстояние от оси вращения до этой массы. Это расстояние называют радиусом r установки дисбаланса. Одинаковые дисбалансы дадут маленькая масса, установленная на большом радиусе и большая масса, находящаяся на маленьком радиусе. При вращении ротора на дисбаланс будет действовать центробежная сила Fц. Она пропорциональна квадрату угловой скорости вращения ротора.

 

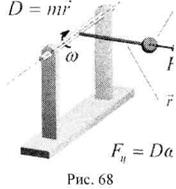
Для того чтобы ротор при вращении находился в динамическом равновесии, центробежная сила должна быть компенсирована силами действующими со стороны опор(реакциями в опорах). Реакции в опорах будут обратно пропорциональны расстояниям от опор плоскости, до плоскости в которой вращается дисбаланс. При установке дисбаланса в середину симметрично ротора при его вращении в опорах возникнут силы равные половине центробежной силы действующей на дисбаланс. Эти силы и вызывают вибрацию опор вращающегося неуравновешенного ротора. Очевидно, что вибрация опоры зависит от ее жесткости и частоты вращения ротора. Если частота вращения ротора совпадет с резонансной частотой опоры, то возникнет резонанс. Далее при незначительном дисбалансе при резонансе опора будет иметь высокую вибрацию. На практике на роторе находится большое число дисбалансов. Вибрация опоры складывается из воздействий, вызываемых каждым из дисбалансов, имеющихся па роторе. Поскольку все дисбалансы расположены в разных угловых положениях и на разных расстояниях от опоры, то при сложении колебаний мы это должны учесть. При измерении вибрации опоры мы имеем результирующий (суммарный) вектор оборотной частоты, в котором автоматически учтены все описанные выше факторы. Еще раз обращаем ваше внимание на то, что гармоническая составляющая вибрации ротора, вызванная дисбалансом, всегда имеет частоту вращения ротора. Задача балансировщика заключается в отыскании по результатам измерений вибрации опор агрегата величины и места установки дисбалансов, которые компенсируют исходную вибрацию опор. Другими словами, система корректирующих масс на роторе должна вызывать вибрацию опор равную исходной и противоположно направленную.

Дисбаланс неизбежно возникает при изготовлении, ремонте и эксплуатации роторов Симметричные детали имеют дисбаланс из-за отклонений от осевой симметрии при изготовлении неоднородности материала. Пазы на роторах имеют отклонение по длине, глубине и ширине Насадные детали роторов, расположенные на диаметрально противоположных сторонах, несколько: отличаются друг от друга по массе и форме. Посадка на ротор деталей с натягом, особенно больших также вызывает дисбаланс вследствие искривления оси вала. Если есть посадочные зазоры, то опять таки мы имеем дисбаланс из-за неоднозначности положения детали в пределах зазора.

В процессе эксплуатации машины также может возникнуть дисбаланс, причиной которого, например, служит поломка лопаток или отложение солей и эрозионный износ ротора и т. д.

 

Типы неуравновешенности

 

Существуют два основных типа неуравновешенности - статическая и моментная. Если они оба присутствуют на роторе, то мы получаем общий случай, который называется динамической неуравновешенностью. При статической неуравновешенности ротора его главная центральная ось инерции параллельна оси вращения ротора, но находится на некотором расстоянии е от нее. Это расстояние называется эксцентриситетом.

Статическая неуравновешенность может быть устранена балансировкой на ножах. Центр масс ротора, находящийся на окружности радиуса е, стремиться переместится в ее нижнюю точку, в которой наступит равновесие сил реакции опор, направленных по вертикальным прямым, проходящим через ось вращения и силы от действия веса, приложенной в центре масс ротора.

 

При моментной неуравновешенности ось инерции ротора пересекается с осью вращения в центре масс ротора. При этом, центр масс ротора находится на оси вращения. Поэтому моментная неуравновешенность не обнаруживается, при статической балансировке. В случае динамической неуравновешенности оси инерции и вращения непараллельные и не пересекаются (другими словами они перекрещиваются).

Для того, чтобы оценить вклад от того или иного типа неуравновешенности, пользуются следующим правилом: полусумма оборотной составляющей вибрации в опорах дает нам вклад от статической неуравновешенности, а полуразность - от моментной.

 

Действительно, симметричная составляющая вибрации оборотной частоты соответствует параллельному смещению главной центральной оси инерции ротора. Половина разности вибрации опор дает кососимметричную составляющую вибрации, которая соответствует чисто моментной неуравновешенности.

 

Условия успешной балансировки

Технология динамической балансировки базируется на нескольких предположениях, которые должны выполняться при постоянной частоте вращения ротора:

• Вибрация оборотной частоты должна быть стабильной во времени и повторяться от пуска к пуску.

• Механическая система должна быть линейна, т.е. приращение дисбаланса вызывает пропорциональное изменение вибрации опор.

• Сдвиг фазы между вызываемой дисбалансом центробежной силой и виброперемещением от этой силы постоянен (не зависит от положения дисбаланса).

Постоянная частота вращения необходима, для того, чтобы центробежные силы, действующие на дисбалансы, были одинаковыми (известно, что центробежная сила пропорциональна квадрату частоты вращения ротора). Постоянство вибрации опор свидетельствует о том, что ротор термически стабилен (прогрет), на нем нет незакрепленных частей, которые могут «болтаться» и занимать от пуска к пуску различные положения на роторе. Линейность механической системы (т.е. нашей машины), нужна для того, чтобы наш метод балансировки давал точные результаты. В противном случае данные пробных пусков не позволят с удовлетворительной точностью уравновесить ротор. Проверить линейность достаточно просто. Для этого при выполнении пробных пусков понаблюдайте за изменением вибрации опор при установке разных масс в одно и тоже место. Пробная масса, увеличенная вдвое, должна давать увеличение изменения вибрации также в два раза. Постоянный сдвиг фазы характеризует также линейность механической системы. Убедится в постоянстве фазы можно воспользовавшись следующим: при изменении угла установки одного и того же груза, фаза оборотной составляющей вибрации должна также отличаться на постоянный угол.

Понятие о коэффициентах влияния

Мы с вами уже знаем, что вибрация опор зависит от величины дисбаланса, его расположения на оси ротора, частоты вращения вала и жесткости опор. При практической работе специалисту необходимо учитывать все эти факторы. Существует метод, который позволяет решить эту проблему, достаточно легко. Суть этого метода заключается в проведении испытаний агрегата, при которых определяют коэффициенты, которые учитывают влияние всех описанных выше факторов от калибровочной массы, установленной в выбранном месте на роторе, на вибрацию опор. В дальнейшем, при балансировке, используют эти коэффициенты для определения места установки и величины корректирующих масс. Эти коэффициенты мы будем называть коэффициентами влияния.

Прежде чем продолжить нашу беседу, имеет смысл договориться об определенной терминологии, которая формализует наши дальнейшие рассуждения. Балансировочной массой будем; называть массу, которую нужно установить на вал, чтобы снизить вибрацию опор ротора до значений, допускающих продолжительную эксплуатацию агрегата. Будем нумеровать их нижним индексом, соответствующим номеру плоскости, в которую мы ее устанавливаем. Плоскостью коррекции будем обозначать плоскость, перпендикулярную оси вращения, в которой мы планируем установить балансировочную массу. Плоскости коррекции нумеруем римскими цифрами в нижнем индексе. Пробной массой будем называть калибровочную массу, используемую при определении балансировочных коэффициентов влияния для выбранной плоскости коррекции. Обозначим ее также как балансировочную массу. Нулевым пуском будем называть данные исходной вибрации опор. Для обозначения нулевого пуска используем нижний индекс «₀». Оборотную составляющую вибрации опор обозначим прописными латинскими буквами А и В. Так, вибрация, измеренная нулевом пуске в опоре А, будет обозначаться как А₀, и соответственно в опоре В через В₀. Напоминаем: оборотная составляющая вибрации опоры определяется ее амплитудой и начальной[30] фазой. И как следствие, при проведении этих измерений необходим отметчик. Пробным пуском будем называть пуск с установленной в выбранной плоскости коррекции пробной массой. Число пробных пусков соответствует числу используемых при балансировке плоскостей коррекции. Номера пусков будем использовать в качестве индексов измеренной на данном пуске вибрации. Обычно номер пуска совпадает с номером плоскости коррекции, в которой установлен пробный пуск. Балансировочным пуском будем называть пуск, с установленными рассчитанными по коэффициентам влияния балансировочными грузами.

Очевидно, что для плоскости коррекции коэффициентов влияния будет столько, сколько направлений для измерения вибрации мы выбрали. Обычно берется по одному направлению (вертикальному) в каждой опоре, т.к. вибрация в опоре в различных направлениях обычно линейно зависима (при условии того, что она вызвана неуравновешенностью). Следовательно, общее число коэффициентов влияния будет равно произведению числа опор машины на число используемых плоскостей коррекции. Для нахождения коэффициента влияния выбранной плоскости коррекции на нужную опору необходимо разделить изменение вибрации в опоре, вызванное этим грузом на его массу.

Другими словами коэффициент влияния представляет собой вибрацию опоры (мкм) от установки единичной массы (один грамм) в выбранной плоскости коррекции в угол равный нулю. Коэффициенты влияния имеют размерность [мкм/г] и обозначаются альфой с двумя нижними индексами (a_IА), первый из которых представляет собой номер плоскости коррекции (I), а второй - опору (А), на которую он оказывает влияние, коэффициент влияния является комплексным числом.

 

 

Понятие о коэффициентах влияния

Давайте посмотрим, как балансируемый ротор реагирует на пробный груз. Сначала представим себе машину с идеально уравновешенным ротором. При его вращении никакой вибрации в опорахнет. Пусть теперь мы установили некую массу в одну из плоскостей коррекции (Рис. 74). Что произойдет в этом случае? Очевидно, что в опорах возникнет вибрация. Значение вибрации полностью определяется величиной и местом установки нашей «пробной» массы. Амплитуда вибрации опор равна произведению модуля соответствующего коэффициента влияния и установленной массы, а фаза определяется как сумма фаз места установки пробного груза и фазы коэффициентов влияния. Эту вибрацию будем называть «вектором влияния пробного груза».

Передвигая пробную массу против направления вращения (Рис. 75), мы будем увеличивать фазу вектора влияния. Причем, фаза вектора влияния должна увеличиваться на угол, равный углу перемещения пробного груза. При этом амплитуда вибрации не меняется.

А теперь давайте посмотрим, что будет происходить с вибрацией машины, ротор которой имеет дисбалансы (Рис. 76). Дисбалансы проявляют себя в виде некоторой результирующей вибрации в опорах. При установке нашего пробного груза вибрация, очевидно, изменится.

 

 

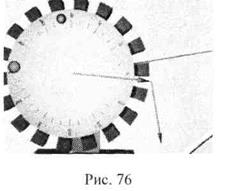
Изменение вибрации будет определяться суммой исходной вибрации ротора и вибрацией, которая у нас возникала при установке пробного груза на идеально уравновешенном роторе. Ясно что, перемещая нашу массу против направления вращения, мы заставим поворачиваться вектор влияния против часовой стрелки, а вектор исходной вибрации при этом меняться не будет. Если мы повернем пробную массу на угол, противолежащий вектору суммарной вибрации опоры, а величину пробного груза изменим таким образом, чтобы длина вектора влияния совпадала с длинной вектора исходной вибрации, то мы сможем компенсировать вибрацию опоры установкой этой массы.

 

Особенности измерения вибрации при балансировке

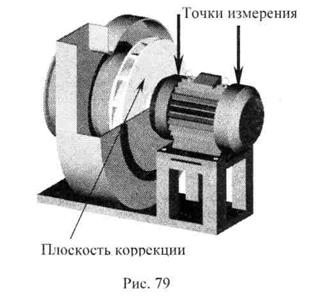
Для выполнения балансировки необходимо правильно измерить амплитуду и фазу оборотной составляющей вибрации. Суть замера заключается в следующем. Из вибрационного сигнала с помощью фильтров выделяют оборотную гармонику. Для этого используют синхронизирующий сигнал (чтобы точно определить частоту вращения ротора). Источником таких сигналов может служить, например лазерный отметчик, который формирует один импульс за один оборот исследуемого ротора. Принцип действия отметчика очень прост. В отметчике вмонтированы лазерный свето- и фотодиод, имеющие общую оптическую ось. Специальная метка[31], нанесенная на ротор, отражает падающий на нее лазерный луч в обратном направлении. На поверхности ротора, в удобном месте наносится специальная метка, отметчик устанавливается напротив метки. При прохождении метки под отметчиком, в нем формируется короткий[32] импульс. Этот импульс жестко привязан к определенному месту (углу) на поверхности ротора, и дает нам один импульс за один оборот ротора. Для дальнейшего описания принципа измерения нужно рассмотреть несколько рисунков:

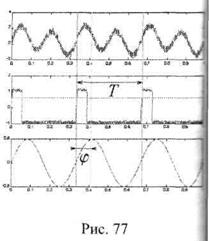
На верхнем рисунке (Рис. 77) представлен исходный вибрационный сигнал, измеренный на опоре, состоящий их первой и второй гармоник оборотной частоты, к которым добавлен широкополосный шум. На рисунке показаны три периода (или оборота) ротора.

Второй рисунок показывает синхронизирующий сигнал с отметчика. Горизонтальная черта на рисунке показывает уровень запуска отметчика. Третий рисунок иллюстрирует отфильтрованный сигнал оборотной частоты, а соответственно j — начальную фазу колебания. Амплитуда гармоники соответствует максимальному значению колебания на обороте. Начало оборота «0°» соответствует прохождению передней кромки метки через луч лазерного отметчика. Обычно метка ставится в радиальной плоскости ротора, которая содержит какие-либо конструктивные особенности, например шпоночную канавку, последнее требование выполнять не осязательно, но желательно. Оно вызвано тем, чтобы вы ставили метку всегда в одно и тоже место (ведь при плохом креплении метка может отлететь).

Фаза вибрации будет соответствовать определенному угловому положению ротора. Углы отсчитываются на роторе от передней кромки метки против направления вращения вала. Для удобства отсчета фазы, на роторе имеет смысл нанести метки через одинаковые интервалы например, через 10°. На облопаченных роторах для этих целей удобно использовать в качестве меток лопатки, предварительно пронумеровав их. При этом метка совмещается с одной из лопаток. Угол между лопатками определяется делением длинны окружности (360°) на число лопаток.

Отметчик должен располагаться вертикально. Датчики также обычно ставят вертикально. При невозможности установки датчиков и отметчика в одной необходимо пользоваться фазовой поправкой.

Для определения поправки нужно рассмотреть следующий рисунок (Рис. 78).

 

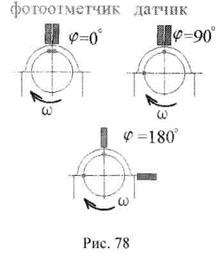
На нем изображены красным цветом отметчик (вертикальный прямоугольник) и метка (точка на роторе), и синим, соответственно, датчик и неуравновешенна масса («тяжелое место»). Если отметчик и датчик вибрации стоят в одной радиальной плоскости (например, вертикально), то тяжелое место будет проходить под датчиком одновременно с меткой и фаза вибрации будет равна 0° (левый верхний рисунок). Пусть теперь масса сдвинута на 90° от метки (углы отсчитываем против направления вращения ротора). Тогда тяжелое место будет проходить под датчиком спустя четверть оборота поен метки, и мы определим истинную фазу (1/4 оборота - 90°) вибрации (правый верхний рисунок). Предположим теперь (нижний рисунок), что датчик установлен на 90° позже отметчика (угол в данном случае считаем по направления вращения!). Фаза измеренная прибором будет равна 180° (!!!), хотя расположение массы и метки на роторе не изменилось. Чтобы учесть такое расположение датчика и отметчика нам необходимо ввести фазовую поправку. Фазовая поправка вычитается из показаний фазы вибрации и отсчитывается от датчика к отметчику против направления вращения. На самом деле, если вы не собираетесь использовать коэффициенты влияния повторно, то. даже не учитывая фазовую поправку (пологая ее равной 0), вы все равно сможете отбалансировать ротор.

Статическая балансировка

Давайте теперь поговорим о статической балансировке. Наверно вы привыкли к тому, что статическая балансировка производится на ножах, т.е. фактически ротор для определения величины статической неуравновешенности даже не крутят, а определяют тяжелое место просто по угловому положению ротора, находящегося в равновесии. Очевидно, что такой метод не подходит даже для точной статической балансировки. При вращении ротора можно с гораздо более высокой точностью определить величину и место статической неуравновешенности.

Давайте обсудим случаи, в которых имеет смысл выполнять только статическую балансировку. Во-первых, такой способ устранения дисбаланса эффективен при балансировке тонких массивных дисков, насажанных на тонких длинных валах. Во-вторых, он подходит для машин, работающих на частотах, гораздо ниже своей первой резонансной частоты.

Прежде чем начать балансировку, давайте поговорим о выборе места расположения плоскости коррекции и измерительных точек. Ясно, что для выполнения статической балансировки

достаточно выбрать только одну плоскость коррекции. Напомним, что статическая неуравновешенность вызывает плоское, параллельное смещение оси инерции относительно оси вращения. Для того, чтобы вернуть ось инерции на ось вращения достаточно приложить одну силу (т.е. воспользоваться одной плоскостью коррекции). Желательно располагать эту плоскость коррекции поближе к центру масс ротора. По той же причине вибрация на опорах будет одинаковой, так что выбираем наиболее удобное место для измерений. Но направление измерений все равно должно совпадать с направлением установки отметчика (желательно вертикальное, в этом направлении, как правило, жесткость опоры выше).

Далее, проверяем выполнение всех описанных выше требований к линейности, постоянству частоты вращения, к стабильности вибрации и т.п. Клеем метку, размечаем углы на роторе, запускаем машину и настраиваем отметчик. Процедура настройки отметчика может происходить в двух режимах: ручном и автоматическом. Для автоматической настройки отметчика на приборе достаточно запустить эту процедуру нажатием одной клавиши (см. инструкцию к прибору). В случае, если по каким-либо причинам,

 

 

Вас не устраивает автоматическая настройка отметчика, то можно воспользоваться ручной регулировкой уровня запуска прибора. Для ручной регулировки порога запуска пользуйтесь клавишами стрелки «вверх» и «вниз», при этом визуально контролируйте положение порога запуска на осциллограмме сигнала отметчика. В случае, если на форме сигнала отметчика отсутствуют синхроимпульсы[33] проверьте правильность установки отметчика. Отметчик должен быть установлен таким образом, чтобы при медленном прохождении метки через луч отметчика наблюдалось свечение контрольного светодиода, расположенного на боковой поверхности отметчика. На этом вся подготовительная работа окончена.

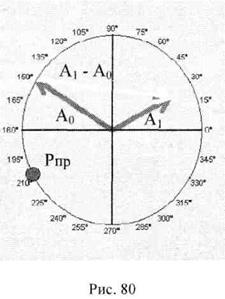
Следующий этап в нашей работе - непосредственно балансировка. Выполняем нулевой пуск. Снимаем амплитуду/фазу первой гармоники в мкм (размах!). Несмотря, на то, что мы в процессе балансировки будем пользоваться результатами измерения вибрации только в одной точке, все равно контролируем вибрацию по всем остальным направлениям (вертикальное, поперечное, осевое на каждой опоре). Рисуем на векторной диаграмме исходную вибрацию. Обозначим ее А₀. Останавливаем машину и устанавливаем пробный груз. Стоп, а как же его выбрать? Оказывается, готовых рецептов не существует. Что касается фазы установки пробной массы, то здесь все относительно просто. Масса ставится в так называемое «нейтральное» место, оно называется так, потому, что при установке в это место вибрация не должна резко вырасти.

 

Это место располагается на радиусе, перпендикулярном фазе вибрации опоры. Кстати, а как вы думаете, фаза вибрации опор в одинаковых направлениях (например, в вертикальном) должна быть в фазе или нет? Правильно, в фазе. Итак, фаза установки пробного груза определяется как фаза вибрации опоры ±90°. Но, вернемся к выбору массы. Величина пробной массы определяется несколькими факторами, такими как величина коэффициентов влияния выбранной плоскости на опоры и уровня исходной неуравновешенности. Поскольку ни первое, ни второе нам неизвестно, то наверняка, величину пробного груза нам сразу не угадать. Ее придется подбирать с тем расчетом, чтобы влияние пробной массы на вибрацию опор было ощутимым. Другими словами, маленькая масса не сможет вызвать ощутимого изменения вибрации, а большая наоборот, вызовет большое изменение, и первое и второе для нас плохо. Малый вес пробного груза даст в наших расчетах большую погрешность, а большой – может привести к появлению нелинейных эффектов в вибрации. Обычно поступают следующим образом: ("берут дисбаланс [г*мм], приблизительно равный 20% от произведения массы ротора [кг] на максимальную по всем направлениям вибрацию опоры [мкм]).

После успешного пробного пуска запишем получившуюся вибрацию А] и нанесем ее на нашу векторную диаграмму. Теперь нам нужно провести несколько расчетов. Сначала мы должны определить разность А₁–А₀, а затем определить коэффициент влияния a=(А₁-А₀)/Р (Р - пробный груз). Теперь мы с вами знаем коэффициент влияния, с его помощью мы найдем балансировочную массу. М=-А₀/a. Знак минус у исходной вибрации взят неслучайно, мы подбираем корректирующую массу таким образом, чтобы исходная вибрация была равна и противоположно направлена вибрации от балансировочной массы. Типичная ошибка в расчете - неправильно берется –А₀. Вместо того, чтобы изменить фазу вектора А₀ на противоположную (т.е. вычесть 180°) обычно! расчете берут отрицательный модуль (!) вибрации. Важно также следить за тем, чтобы ради» установки пробной и корректирующих масс был одинаковым.

Ну что же, масса найдена и установлена. Делаем контрольный пуск. Его задача оценить остаточную неуравновешенность и при необходимости, провести дополнительный балансировочный пуск. Оценка остаточной неуравновешенности будет предметом отдельной беседы. Что касается дополнительного балансировочного пуска, то, при его необходимости, используют готовый (уже рассчитанный) коэффициент влияния и вибрацию контрольного пуска, по ним рассчитывают дополнительную балансировочную массу. Причем, первую балансировочную массу, установленную ранее оставляют на своем месте.

 

 

Динамическая балансировка

Ну что ж, осталось. поговорить о динамической балансировке. В отличие от статической балансировки, в; которой мы использовали одну плоскость коррекции, здесь мы будем работать с двумя плоскостями. Чтобы устранить моментную неуравновешенность, т.е. создать компенсирующий момент, необходимо иметь минимум две плоскости коррекции. Динамическая балансировка позволяет полностью (в известных рамках) устранить вибрацию опор. Она эффективна для большинства роторов, работающих между своими первой и второй резонансными частотами опор. В более сложных случаях пользуются специальными методами балансировки, о которых в этом курсе мы говорить не будем. Выбор плоскостей коррекции на агрегате обычно заранее предрешен конструктором. В конструкцию ротора закладываются две плоскости, конструктивно содержащие места под установку корректирующих масс. Обычно они расположены на торцевых плоскостях бочки электродвигателя или, скажем, на крайних дисках компрессора и т.д. Если нужно выбрать плоскость самому, то пользуются следующим правилом. Коэффициенты влияния, определяемые для выбранных плоскостей коррекции должны разделяться. Другими словами они должны отличаться друг от друга. Это необходимо для того, чтобы машина чувствовала разницу между плоскостями коррекции. Ведь, если коэффициенты влияния одинаковые, то это формально означает, что плоскость коррекции одна и та же.

А отсюда следует, что убрать динамическую неуравновешенность этими плоскостями не получится. Нужно подобрать другие плоскости коррекции.

Поскольку нам нужно при балансировке использовать две плоскости, то общее число пробных пусков увеличится. Их должно быть три. Первый - нулевой, в нем мы обязательно должны использовать вибрацию обоих опор. Во время второго пуска, с пробным грузом в первой плоскости, мы определяем изменение вибрации от пробного груза в обоих опорах. Это необходимо потому, что в отличие от статической, коэффициенты влияния плоскости коррекции на разные опоры будут сильно отличаться друг от друга. По окончании измерений нужно не забыть снять пробный груз из первой плоскости. Третий пуск нам позволит определить коэффициенты влияния для второй плоскости коррекции.

Об выборе величины пробного груза мы говорили с вами в разделе, посвященном статической балансировке, там же мы обсудили как размечать углы на роторе, установить датчик и отметчик, поэтому не будем здесь подробно на этом останавливаться. Из-за того, что вибрацию нужно контролировать в обоих опорах, то датчик последовательно переставляется с опоры на опору.

 

Рассмотрим подробно последовательность измерений:

• Выполняем нулевой пуск, в результате имеем исходную вибрацию опор А₀ и В₀.

• Устанавливаем пробный груз в первую плоскость Р₁ и снова измеряем вибрацию опор А₁ и В₁

• Вычисляем изменение вибрации в опорах, вызванное установкой пробного груза Р₁

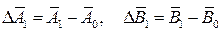
• Рассчитаем коэффициенты влияния первой плоскости на опоры А и В:

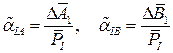
• Снимем пробный груз с первой плоскости коррекции и установим его во вторую плоскость. Обозначим его Р_II.

• Выполним второй пробный пуск, измерим вибрацию в опорах А и В.

• Рассчитаем изменение вибрации в опорах относительно нулевого пуска:

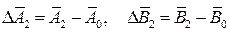v

• Определим коэффициенты влияния второй плоскости коррекции на опоры:

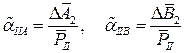
• Удалим второй пробный груз.

После того, как мы определили все четыре коэффициента влияния, нужно с их помощью подобрать необходимые балансировочные массы М, для обеих плоскостей коррекции. Составим уравнения, которые помогут это сделать. Так как нам известны коэффициенты влияния, или другими словами вклад в вибрацию опор от плоскостей коррекции, то мы можем составить уравнения, определяющие вибрацию в каждой опоре. Для опоры А это уравнение будет иметь вид:

 

 

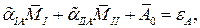
где ε_А- остаточная вибрация в опоре А. Аналогично, для второй опоры (В):

Задача балансировки состоит в минимизации остаточной вибрации е в обоих опорах. Объединив эти векторные уравнения в систему, и учитывая, что остаточная вибрация ε, должна быть равна нулю, получим:

 

(*)

 

• Теперь мы должны решить систему из двух векторных уравнений (*). Решение системы нам даст искомые балансировочные массы для каждой плоскости коррекции. Обычно решение это системы выполняется с помощью балансировочной программы, встроенной в анализатор вибрации. Поэтому, подробно на способе решения этой системы мы останавливаться не будем.

• Устанавливаем балансировочные массы в соответствующие плоскости коррекции и выполняем контрольный пуск. Вибрация, полученная при контрольном пуске А₃ и В₃, может использоваться для расчета дополнительных балансировочных масс с помощью уравнений (*). В правую часть которой вместо исходной вибрации А₀ и В₀ подставляют вибрацию, полученную при контрольном пуске А₃ и В₃.

• Проведем добалансировку при помощи дополнительных балансировочных масс. При эта массы, установленные перед контрольным пуском мы оставляем на роторе.

Обращаем ваше внимание, на то, что не всегда имеется возможность устанавливать корректирующие массы, иногда имеет смысл с противоположной стороны места установки (180°) корректирующего груза удалить такую же массу.

 

Оценка допустимой остаточной неуравновешенности

 

Одина из проблем любой балансировки связана с принятием решения об ее окончании. Затраты на балансировку с повышением ее точности растут достаточно быстро, а экономический эффект от высокой точности балансировки не столь ощутим, поэтому есть момент в процессе балансировки, достигнув которого рационально остановится.

Как правило, нормируется величина остаточной неуравновешенности в зависимости от типа и рабочей частоты агрегата. Сначала вы должны выбрать класс точности балансировки. На сегодняшний день существует достаточно большое число классов точности балансировки. Класс точности определяется для определенного типа агрегатов и учитывает типичные условия их нагружения и эксплуатации, а так же допустимые уровни вибрации оборудования. Вот некоторые из них: 016 -приводы специального назначения, детали двигателей, коленчатые валы, части сельскохозяйственных машин и дробилок; С6.3 - рабочие колеса насосов и вентиляторов, ротора электромашин общего назначения: 02.5 - паровые и газовые турбины, турбокомпрессоры, приводы станков, маленькие и специальные ротора электромашин; 01 - маленькие ротора электромашин и приводов специального назначения, О0.4 – прецизионные шлифовальные колеса, гироскопы. После того, как мы с вами выбрали класс точности, воспользуемся приведенной ниже диаграммой для оценки допустимой остаточной неуравновешенности ротора.

Пользуются диаграммой следующим образом: по горизонтали находим рабочую частоту нашего агрегата, проводим через нее вертикальную прямую до пересечения с наклонной прямой соответствующей нашему классу точности. Затем через точку их пересечения проводят горизонтальную прямую и на вертикальной оси отсчитывают значение допустимой остаточной неуравновешенности. Допустимая остаточная неуравновешенность нормирует удельный дисбаланс, который равен смещению центра масс или эксцентриситету.

Полученное из диаграммы значение дает значение суммарного удельного остаточного дисбаланса, поэтому его надо умножить на массу [кг] балансируемого ротора, в результате мы получим допустимый остаточный дисбаланс [гмм]. Его обычно делят на число плоскостей коррекции, и, зная радиусы [мм] установки корректирующих масс в каждой из них, рассчитывают допустимые остаточные массы [г].

Рекомендуемая литература

1. Абашидзе А.И. "Динамика фундаментов паровых турбин" Л. ГЭИ.. 1960 г.

2. Абалаков Б.В. Банник, В.П, Резников Б.И. Монтаж паровых турбин и вспомогательного оборудования М. Энергия, 1966 г.

3. Биргер И.А. Техническая диагностика М. Машиностроение 1978 г.

4. Брановский М.А. и др. Исследование и устранение вибрации турбоагрегатов. М. Энергия, 1969 г.

5. Генкин М.Д., Соколова А.Г. Виброакустическая диагностика машин и механизмов. М. Машиностроение, 1987 г.

6. Гольдин А.С.. Львов М.И., Урьев А.В. Тепловые деформации гибких роторов в подшипниках скольжения. Энергомашиностроение. 1983 г.. №5

7. Ден-Гартог Д. П. Механические колебания. М. Физматгиз, 1960 г.

8. Дон Э.А., Осоловский В.П. Расцентровка подшипников турбоагрегата. М. Энергоатомиздат 1994 '

9. Кальменс В. Я. Обеспечение вибронадежности роторных машин. Санкт-Петербург, 1992 г.

10. Карасев В. А., Ройтман А.Б. Доводка эксплуатируемых машин. Вибродиагностические методы. М., Машиностроение, 1986 г.

11. Лисицин И.С. Уравновешивание роторов турбоагрегатов. "Вестник электропромышленности" 1962 г.

12. Методические указания по контролю вибрации питательных центробежных насосов. РД 34.41.301-89.

13. Микунис СИ. Опыт вибродиагностики турбопитательных насосов энергоблоков 250 и 300 Мвт.

14. Микунис СИ., Кравец А. И. Частотный спектр крупных теплофикационных турбин как средство технической диагностики. "Энергетик" 1987 г. №10

15. Молочек Е.А. Ремонт паровых турбин. М„ Энергия. ] 968 г.

16. Олимпиев В.И. Собственные и вынужденные колебания роторов на подшипниках скольжения. Труды ЦКТИ, 1962 г.

17. Правила технической эксплуатации'электрических станций и сетей. Энергия, 1966 г.

18. Рунов Б.Т. Исследование и устранение вибрации паровых турбоагрегатов. М. Энергоатомиздат 1982 г.

19. Салимон А.В., Тараканов В.М. Об уменьшении количества балансировочных пусков при многоплоскостной балансировке валопроводов турбоагрегатов. М. "Электрические станции" №1. 1978 г.

20. Станиславский Л.Я, и др. Вибрационная надежность мощных турбогенераторов.

21. Теория и конструкция балансировочных машин, Машгиз 1963 г.

22. Трунин Е.С., Сацук В.В. Анализ динамических коэффициентов влияния современных турбоагрегатов. Известия Академии Наук Каз. ССР. Серия физико-математическая, №1. 1973 г.

23. 22 А. с. № 503337 (СССР). Способ снижения вибрации явнополюсной машины. Трунин Е.С, приоритет от 27.11.72, опубликовано 15.02.76 г.

24. Трунин Е.С, и др. Методы вибродиагностики тягодутьевого оборудования "Электрические станции" №6. 1986 г.

25. Трунин Е.С, Хасанов Р.А. Диагностика вибрационного состояния силовых трансформаторов

 

Новая литература (за последние 20 лет)

1. Астахов Николай Владимирович. Математическое моделирование вибраций асинхронных машин. -1987

2. Астахов Николай Владимирович. Учебное пособие по курсу Вибрация и шум электрических машин. Магнитные вибрации синхронных машин. - 1987

3. Барков Алексей Васильевич. Шум и вибрация судового электрооборудования. - 1985

4. Белоусова Нина Никоновна. Методы и средства защиты от вибрации. - 1996

5. Болотин В.В. Вибрации в технике. - Т.1: Колебания линейных систем. - 1999

6. Буренин В.В. Резиновые амортизаторы для виброизоляции машин, агрегатов, механизмов и приборов. - 1996

7. Вибрации в технике: Справочник. – М.: Машиностроение, 1995 – Т. 6: Защита от вибрации и ударов / [В.К. Асташев и др.]; Под ред. К.В. Фролова

8. Вибрации трубопроводов электрических станций и методы их устранения. - 1992

9. Вибрации центробежных нагнетателей природного газа. Нормы и методика оценки вибрационного состояния. -1990

10. Вибрационная надежность паротурбинных агрегатов. - 1986

11. Вибрационная техника. - 1987

12. Вибрационная техника. - 1988

13. Вибрационная техника. - 1989

14. Вибрация и вибродиагностика. Проблемы стандартизации. - 1991

15. Вибрация и диагностика машин и механизмов. - 1990

16. Вибрация мостовых электрических кранов и методы борьбы с ней. - 1989

17. Вибродиагностика и виброзащита машин и приборов. - 1989

18. Волновые и вибрационные процессы в машиностроении. - 1989

19. Волновые и вибрационные процессы в машиностроении. - 1989

20. Вопросы виброзащиты и вибротехники. -1990

21. Всесоюзная научно-техническая конференция Современное состояние и перспективы развития методов и средств виброметрии и вибродиагностики (3-5 окт. 1989 г., Минск). - 1989

22. Грибков А.М.. Расчет колебаний валов гидромашин. - 1998

23. Гусаров Анатолий Александрович. Динамика и балансировка гибких роторов. - 1990

24. Дефектоскопия и вибродиагностика. - 1988

25. Динамика виброактивных систем и конструкций. - 1989

26. Динамические испытания и контроль механических систем. - 1988

27. Елисеев П. Г.. Датчики малых смещений и вибраций на основе полупроводниковых лазеров. -1991

28. Кельзон Анатолий Саулович. Управление колебаниями роторов. - 1992

29. Клюкин Игорь Иванович. Физико-технические основы виброизоляции механизмов и другого виброактивного оборудования. - 1987

30. Коровин Юрий Васильевич. Балансировка роторов. - 1994

31. Курчавова Татьяна Павловна. Измерение вибрации машин на производстве. - 1991

32. Макаева Р.Х.. Исследование вибрационных характеристик деталей и узлов двигателей методом голографической интерферометрии при их диагностике. - 1998

33. Маслов Георгий Сергеевич. Колебания в машинах и методы виброзащиты. -1987

34. Методология нормирования интенсивности вибрации узлов ГПА по статистике штатного контроля. - 1996

35. Методы и средства виброакустической диагностики машин. -1988

36. Мижидон А.Д.. Синтез параметров виброзащитных систем. - 1997
3". Назаров В.П.. Балансировка роторов турбонасосных агрегатов. - 1995

38. Нормирование дисбалансов шпиндельных узлов. - 1989

39. Оценка технического состояния зубчатых передач по параметрам виброактивности в цеховых условиях. - 1990

40. Перевощиков СИ.. Гидродинамическая вибрация насосных агрегатов. - 1997

41. Применение средств вибропоглощения и виброгашения в промышленности и на транспорте. -1988

42. Применение средств вибропоглощения и виброгашения в промышленности и на транспорте. -1990

43. Проскуряков К.Н.. Использование виброакустических шумов для диагностики технологических процессов в АЭС. - 1999

44. Прочностные и динамические характеристики машин и конструкций. - 1989

45. Пучкин А. Е.. Методы предотвращения кавитаци и, вибрации и шума в гидроприводах металлургического оборудования. - 1989

46. Рекомендации по определению прямым методом динамических усилий, развиваемых вибровозбудительными системами, используемыми при вибрационных испытаниях основного оборудования и сооружений 'ГЭС и ГЭС. - 1995

47. Рекомендации по проектированию виброизоляции обогатительного оборудования. - 1989

48. Родионов Леонид Васильевич. Вибрация и виброзащита машин. - 1990

49. Саакян Эдуард Смбатович. Уравновешивание и виброзащита механизмов. - 1985

50. Семенов Юрий Алексеевич. Теория механизмов и машин. Колебания и балансировка роторов. 1995

51. Снижение вибраций машин. - 1994

52. Совершенствование конструкций подшипников и методов их выбора, исследования виброакустических характеристик подшипников.-2. - 1991

53. Современные численные методы исследования вибраций машин. - 1991

54. Справочник по балансировке. - 1992

55. Технология балансировки роторных агрегатов.-Ч.1: Основные сведения из теории балансировки роторов. - 1998

56. Цыфанский Семен Львович. Практическое использование нелинейных эффектов в вибрационных машинах. - 1992

57. Швейкин Александр Петрович. Ударная и вибрационная защита машин. - 1988

58. Швецов Владимир Тимофеевич. Внешнее уравновешивание моментов сил в машинах. - 1996

 

 

[1] Векторная диаграмма это графическое изображение значений физических величин, изменяющихся по гармоническому закону, и соотношений между ними в виде векторов.

[2] Колебания различной частоты на векторной диаграмме будут двигаться друг относительно друга со скоростью, определяемой разностью их частот.

[3] Противоположная фаза - фаза отличающаяся от исходной на 180°.

[4] Комплексное число, число вида х+iу, где х и у – действительные числа, а; i – т. н. мнимая единица (число, квадрат которого равен -1); х называется действительной частью, а у – мнимой частью комплексного числа. Действительные числа – частный случай комплексных чисел (при у =0). Комплексные числа, не являющиеся действительными (у ¹ 0), иногда называются мнимыми числами, при х= 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число х+iу изображается точкой плоскости, имеющей прямоугольные координаты х и у. Если полярные координаты этой точки обозначить через r и j, то соответствующее комплексное число можно представить в виде: r (cosj + i sinj) (тригонометрическая форма комплексного числа); называется модулем комплексного числа х+iу, а его аргументом, или в экспоненциальном виде: re ^ij

[5] Пропорциональность, простейший вид функциональной зависимости. Различают прямую пропорциональность. (y=kx) обратную пропорциональность (y=k/x).

[6] Кинетическая энергия, энергия механической системы, зависящая от скоростей движения составляющих ее

частей ()

[7] Временная область – область, в которой сигнал рассматривается в зависимости от времени.

 

[8] ИРРАЦИОНАЛЬНОЕ ЧИСЛО, число, не являющееся рациональным, т. е. не могущее быть точно выраженным дробью m/n, где m и n – целые числа.

[9] Акселерометр (от лат. ассе1его –ускоряю и...метр) датчик для измерения ускорения.

[10] Велометр (от лат. velocitas - скорость и...метр) датчик для измерения скорости.

[11] Проксиметр (от лат. proximus – ближний и...метр) датчик для измерения смещения, раньше их называли виброметрами

[12] ЭДС - электродвижущая сила.

 

[13] Резонансная область обычно имеет ширину, приблизительно равную#0% от резонансной частоты. Другими словами от 0,8 f _Р до 1,2 f _Р.

 

[14] Наличие краски уменьшает твердость поверхности и

[15] Аутентичный текст (от греч. authentikos – подлинный), текст документа, официально признанный равнозначным другому тексту, составленному, как правило, на другом языке, и имеющий одинаковую с ним юридическую силу.

[16] Гибким будем называть ротор, частота изгибных колебаний которого ниже рабочей частоты вращения.

[17] Вероятность, в математике – числовая характеристика степени возможности появления какого-либо случайного события при тех или иных определенных, могущих повторяться неограниченное число раз условиях.

[18] Регрессия – зависимость среднего значения какой-либо величины от некоторой другой величины.

[19] По общему уровню

[20] связь

[21] структурированной

[22] За исключением особо оговоренных случаев

[23] Спектр (от лат. spectrum – представление, образ) в физике, совокупность всех значений какой-либо физической величины, характеризующей систему или процесс. Чаще всего пользуются понятиями частотного спектра колебаний

[24] F – частота выборки

[25] Нормальным агрегатом будем считать агрегат, на котором выполняются следующие условия: вибрация в контролируемых точках соответствует нормам;

диагностические параметры находятся в пределах, соответствующих заданному режиму работы агрегат на стационарном режиме наблюдается стационарная вибрация: параметры ее изменчивости находятся в пределах, характерных для заданного режима; отсутствуют существенные внезапные изменения вибрации; отсутствует существенный монотонный рост вибрации во времени (тренд); отсутствует низкочастотная вибрация; отсутствуют существенные изменения спектрального состава вибрации.

[26] Несущая – частота гармонической функции, которую мы модулируем.

[27] Октава - единица частотного интервала, равна интервалу между двумя частотами (f₁ и f₂), логарифм отношения которых, что соответствует.

[28] Дис... (франц. des)- приставка, обозначающая отсутствие

 

[29] Баланс (франц. balance, букв. — весы)- равновесие, уравновешивание.

[30] Далее прилагательное «начальная» для краткости опускаем

[31] В принципе лазерный отметчик может работать на любых отражающих поверхностях, имеющих контрастный переход отражающих свойств поверхности.

[32] Длительность импульса определяется линейной скоростью метки относительно луча.

[33] Синхроимпульс – скачек уровня сигнала, формируемого отметчиком, возникающий при прохождении лучом.